Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Движение товара от производителя к потребителю становится таким сложным, что не может поддерживаться только производителями. Появляются разветвлённые  посреднические сети, которые можно представлять в виде связных конечных ориентированных графов. Структура этих сетей играет решающую роль в определении того, какие именно товары будут предлагаться на том или ином рынке, то есть конкурентоспособность товаров и объёмы потребления в различных регионах.

Региональный потребительский рынок - сложная пространственно-экономическая система, состоящая из многочисленных элементов и связей между ними, поэтому изучение этого рынка предполагает анализ закономерностей и факторов, определяющих его формирование и развитие, комплексное рассмотрение всех аспектов рынка [5]. Цены на региональном потребительском рынке существенно различаются в пространстве, что обусловлено влиянием системы региональных факторов. Одним из таких существенных факторов является этнокультурный потенциал.

При рассмотрении конкурентоспособности с позиции этнокультурного потенциала сибирских регионов необходим комплексный подход в исследовании потребительского рынка. В частности, востребованы решения, направленные на изучение территориальной структуры спроса и предложения товаров и услуг, определение объемов поставок через посредников и цен в конкретных территориальных зонах.

Развитие регионального потребительского рынка Сибири связано с изменениями и структурными сдвигами в потреблении и торговле под влиянием научно-технического прогресса, информатизации общества, этнокультурного фактора торговли потребительскими товарами, а также изменениями в пространственной организации потребительского рынка. Этнокультурная составляющая повышения конкурентоспособности региона является неотъемлемой частью анализа потребительского рынка Сибири, представляющего собой совокупность фирм, вовлеченных в куплю-продажу потребительских товаров в пределах определенной рыночной зоны. Потребительский рынок сибирского региона, имеющий огромную географическую территорию с невысокой плотностью населения, включает в себя фирмы, которые осуществляют торгово-посредническую деятельность, хранение, транспортировку, реализацию товаров, страхование и др. При этом он имеет систему прямых, обратных и комбинированных связей, обеспечивающих потоки товарных, финансовых, информационных ресурсов, осуществление переговоров, заказов и платежей и др. Все эти аспекты функционирования рынка накладывают отпечаток на пути решения задачи продвижения товаров.

Поэтому задача анализа и учёта продвижения по торговым сетям товаров и донесения их до конечного потребителя приобретает существенное значение. Актуальность работ в данном направлении подтверждается востребованностью в разработке и применении различных математических моделей. Последние позволили бы оценить динамику процесса купли-продажи, выявить реакции поведения системы «покупатель - продавец» к воздействию неустойчивых параметров, таких как цена, объём продаж. 

Далее предлагается к рассмотрению созданная на основе обыкновенных дифференциальных уравнений математическая модель, описывающая взаимосвязи и устойчивое поведение подсистемы «покупатель - продавец», входящей в торгово-посредническую систему.

Системность закономерностей протекания тока в электрической цепи послужила стартовым моментом в исследовании распределения товарных потоков. Постановка задачи исследования системы «продавец - покупатель» представлена в работах [1-3], где установлено соответствие между закономерностями продвижения товара в торгово-посреднической сети и законами Ома и Кирхгофа в электрических цепях, между силой взаимодействия двух микрорынков и законом тяготения Ньютона. Эти соотношения предоставляют возможность анализировать значения параметров микрорынка торговой системы, рассматривая её как структуру, состоящую из цепей последовательно или параллельно соединённых элементов.

Торговая система однопродуктового рынка представима в виде сети, включающей в себя такие субъекты (элементы), как продавцы, посредники и конечные потребители. Движение товара происходит от производителя (продавца) к потребителю (покупателю) без учёта потерь при доставке под воздействием основных рыночных факторов: спроса, предложения. Объём продукта, произведённого в рынке, равен объёму потребления.

Исходя из гипотезы общности законов экономических и физических процессов, уравнения соединения элементов между собой составляются на основе законов сохранения материального потока в узле сети, сохранения стоимости, спроса и предложения, Ома и Кирхгофа.

Потоковые процессы в сети можно рассматривать в статике и динамике. Для моделирования динамической модели выбирается такой инструмент, как обыкновенные дифференциальные уравнения. Решая их, можно определять цены в узлах торговой сети и объёмы товара, протекающего по ветвям, исследовать устойчивость взаимосвязи покупателя и продавца. 

Проблема равновесия, устойчивости, существования устойчивого равновесия потоковых процессов является ключевой при анализе различного вида систем. Экономические теории исследуют (с применением математического аппарата) состояния равновесия экономических систем и ограничиваются высказываниями, когда речь заходит о кризисах и прочих неустойчивых состояниях в экономике. Известно, что цены не находятся в равновесии, а постоянно совершают колебания. В то же время колебательное движение происходит не произвольно, а вокруг этой самой неустойчивой равновесной точки, следовательно, само движение является устойчивым [4].

Рассмотрим приложение теории обыкновенных дифференциальных уравнений к задаче описания вышеупомянутых экономических процессов.

Модель функционирования подсистемы «продавец - покупатель» сети реализации топлива в республике Хакасия

Рынок топлива выбран в качестве объекта, удобного для приложения предлагаемой модели. Пространственно-временные масштабы его существования позволяют рассматривать систему как непрерывную проводящую среду с устанавливающимися потоками при t → ∞.

Ежедневные изменения объёмов продаж бензина зависят от различных событий: праздничные и выходные дни, климатический и сезонный фактор, объём закупок, цена и динамика переработки нефти, психологические особенности поведения людей, этнокультурное состояние общества и др. Эти факторы учитываются при вычислении коэффициентов, которые позволяют охарактеризовать субъекты торговой сети и учесть их потенциальные возможности в продвижении товара.

Моделирование проводилось с использованием аналитических методов решения обыкновенных дифференциальных уравнений и численных методов, с помощью программ Mathcad и Matlab.

Предложим к рассмотрению подсистемы: 1) «продавец - конечный потребитель»; 2) «продавец - покупатель (посредник)»; 3) «посредник - конечный потребитель».

Рассмотрим цепь, входящую в структуру сети и состоящую из последовательно соединённых элементов «продавец - конечный потребитель», которую можно описать системой (1) обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами через функции объёма Q(t) и цены p(t)

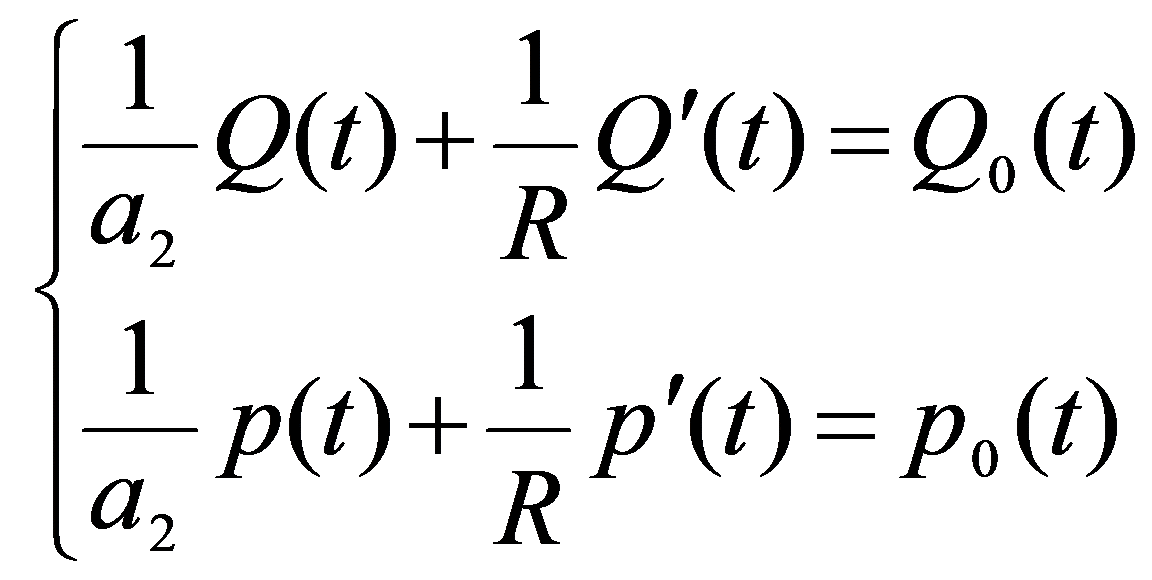  , (1)

с начальными условиями , .

Для данной цепи покажем реализацию решения системы (1). На основе статистических данных (табл. 1), рассматривая увеличение цены продаж с 6 по 8 неделю на 0,5 руб., принимаются следующие значения начальных условий: p₀ = 19,00 руб., p_y = 19,50 руб., Q₀ = 1602,55 л, Q_y = 1642,50 л. Определяются коэффициенты: 1) характеризующий скорость изменения объема от изменения цены: a₂= 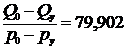>0; 2) эластичности предложения по цене: 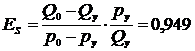>0; 3) проводимости товара по цепи: 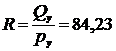. При шаге моделирования ∆t₁ = 1 нед., время переходного процесса составило Т = 10 нед.

Таблица 1 - Моделирование подсистемы «продавец - конечный потребитель»

Для оценки точности математической модели, то есть степени совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели, использовалась относительная погрешность модели:

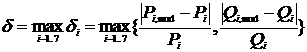, => δ  = 13,07 %.

Возможное время моделирования i = 7, так как по действительным данным при  i = 8 происходит изменение цены.

При изменении цены продавца в процессе купли-продажи наблюдается движение к устойчивому состоянию (рис. 1), где пунктирной линией указаны действительные данные, сплошной - модельные значения. Значения Q₀ < Q_у и P₀ < P_у, следовательно, функции цены и объёма возрастают до установившихся значений.

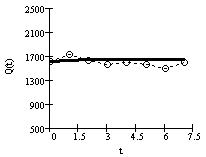
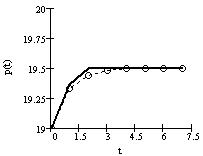
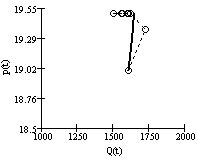
а)                                          б)                                         в)

Рис. 1. Изменения функций во времени:

а) цены P(t); б) объёма Q(t); в) на плоскости (Q(t),P(t)).

Если возможности продавца обеспечивают высокую проводимостью товарного потока R>>0 и коэффициент а₂ в функции предложения p_S(Q,t) =  будет иметь малую величину, то коэффициент эластичности E_S близок к нулю. При этом функция предложения описывает микрорынок, на котором присутствует монополия продавца. На рассматриваемом рынке функция р(t) достигнет значения р_у за малый промежуток времени. Это свидетельствует о практически неограниченных возможностях продавца, способного быстро довести цену до установившегося (желаемого) значения.

При  малой величине проводимости R (характерной для фирм, относящихся к малому бизнесу) и а₂ >> 0, => E_S >> 0. Функция предложения отвечает условиям существования чистой конкуренции продавца. На данном микрорынке продавцу требуется гораздо больше времени для доведения цены до р_у, поскольку из-за малых объемов реализации товара он не способен повлиять на конечного потребителя.

Рассмотрим цепь при последовательном соединении «продавец - покупатель (посредник)», которая описывается системой (2) обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами:

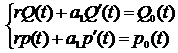,   (2)

с начальными условиями , .

Рассматривая уменьшение цены продаж с 4 на 5 неделю (табл. 2) на 0,073 руб.,  принимаются следующие значения: 1) начальные данные p₀ = 13,358 руб., p_y = 13,285 руб., Q₀ = 33620,0 л., Q_y = 36900,5 л; 2) коэффициент, характеризующий скорость изменения цены от изменения объёмов потребления: , = 0,000022 > 0; 3) коэффициент эластичности спроса по цене: ,= 0,0618 > 0; 4) коэффициент резистивности: 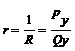= 0,00037.

Таблица 2 - Моделирование подсистемы «продавец - покупатель (посредник)»

При шаге моделирования ∆t₁ = 1 нед., время переходного процесса составило Т = 1 нед., относительная погрешность модельных значений δ = 15,21% при возможном  времени моделирования i = 4.

При изменении цены в подсистеме «продавец - покупатель (посредник)» наблюдается движение к устойчивому состоянию (рис. 2), где пунктирной линией указаны действительные данные, сплошной - модельные значения. Значения p₀ > p_у и Q₀ < Q_у, поэтому, функция p(t) убываeт, а функция Q(t) возрастает до соответствующих установившихся значений.

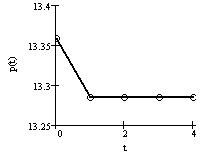
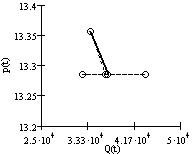
 а)                                                      б)                                            в)

Рис. 2. Изменения функций во времени:

а) цены p(t); б) объёма Q(t); в) на плоскости (Q(t),p(t)).

Для крупного покупателя (посредника), обладающего R_пок >> 0 (с малыми значениями а₁ и E_D), спрос по объему продаж не эластичен. Такой покупатель является монополистом в приобретении товара, и для достижения объемов покупки Q_пок  до Q_у ему требуется незначительное время.

Если покупатель обладает малой величиной проводимости R_пок , коэффициенты а₁ >> 0 и E_D >> 0, то функция спроса характеризует микрорынок как рынок чистой конкуренции среди покупателей. На данном микрорынке покупателю требуется значительное время для доведения объемов продаж до установившегося значения.

При последовательном соединении цепи «посредник - конечный потребитель», где посредник выступает как покупатель и продавец, составлена система обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами:

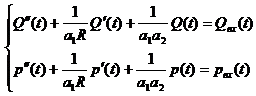,  (3)

с начальными условиями , .

Исходные данные удобнее представить в относительных единицах, тогда 1) коэффициент, характеризующий посредника-покупателя как скорость изменения цены в зависимости от изменения объемов потребления товара: a₁ = 0,4002; 2) коэффициент, характеризующий посредника-продавца как скорость изменения объёма в зависимости от изменения цены товара: a₂ = 1,605; 3) коэффициент проводимости R = 1; 4) начальные данные p₀ = 0,678, p_y = 1,00, Q₀ = 1,0110, Q_y = 1,00, , .

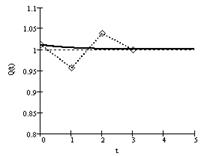
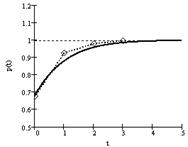
Характеристическое уравнение соответствующих дифференциальных уравнений  имеет корни λ₁ = -1,184, λ₂ = -1,315, поэтому система устойчива асимптотически и при  функции p(t) → p_y и  Q(t) → Q_y. При шаге моделирования ∆t₁ = 1 нед., время переходного процесса Т = 7 нед. Относительная погрешность модельных значений  δ = 11,9% при возможном времени моделирования i = 3 (табл. 3).

Таблица 3 - Моделирование подсистемы «посредник - конечный потребитель»

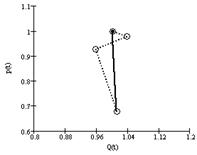
При изменении цены в системе «продавец - конечный потребитель» наблюдается движение к устойчивому состоянию (рис. 3), где пунктирными линиями указаны действительные данные, сплошной линией - модельные значения.

При Q₀ > Q_у  функция объёма во времени убывает до Q_у, при p₀ < p_у  функция цены во времени возрастает до p_у.

                  а)                                           б)                                        в)

Рис. 3. Изменения функций во времени:

а) цены p(t); б) объёма Q(t); в) на плоскости (Q(t),p(t)).

Основные результаты и выводы

Основываясь на теории линейных электрических цепей, теории спроса и предложения, опираясь на принципы и методологию экономической физики, разработана математическая модель динамики цен и объёмов продаж.

На основе анализа продаж топлива относительная погрешность модели при шаге моделирования в 1 неделю составляет в среднем 6,01% в период от 3 до 7 недель, что демонстрирует соответствие с практической динамикой. Это является дополнительным аргументом важности и актуальности развития и применения методов математического моделирования сложных экономических систем с использованием теорий электрических цепей и обыкновенных дифференциальных уравнений. centerem; 

На основании полученной математической модели оценена устойчивость взаимосвязи «продавец - покупатель», что позволяет выявить границы возможностей функционирования субъектов рынка.

Дальнейшие исследования в решении задачи устойчивости и управления в торгово-посреднических системах внесут существенный вклад в развитие теории и практики кибернетического подхода в функционировании конкурентного рынка товаров.

Исследование осуществлено при поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг. (госконтракт № 02.740.11.0585).

Рецензенты:

• Нагрузова Л.П., д.т.н., профессор кафедры «Строительство» Хакасского технического института - филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан.
• Булакина Е.Н., д.т.н., профессор кафедры «Автомобили и автомобильное хозяйство» Хакасского технического института - филиала ФГАОУ ВПО «Сибирского федерального университета», г. Абакан.

Работа получена 26.10.2011