Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Исследование на разрешимость неклассических краевых задач для линейного дифференциального уравнения второго порядка, а также локальных краевых задач для нагруженного линейного дифференциального уравнения приводит к необходимости поточечной оценки решения локальных краевых задач для оператора Штурма-Лиувилля.

В настоящей работе исследуется поведение решения краевой задачи первого рода

,                                            

,                                                         

где  коэффициенты и правая часть уравнения  удовлетворяют условиям 

 всюду на . Как известно, при условиях , , задача  однозначно разрешима в классе функций  и для её решения имеет место априорная оценка в равномерной метрике

            Знание верхних оценок   и , в случае знакоопределенности правой части , позволяет получить поточечную оценку , которая применяется для  усиления оценки

Получим оценку решения задачи  в точке . С этой целью воспользуемся представлением этого решения [3],[4]

,                                      

где   функция Грина первой краевой задачи для уравнения .

     Функция  определяется по формуле:

                     

где  решения задач

,            (6)    

,            (7)    

Постоянная  в  определяется по формуле

.                                      

В силу краевых условий,

.                                         

Рассмотрим два уравнения:

                                                   (9)

                                                   (10)

где функции  и  вещественны и непрерывны на

интервале  и  При этих условиях уравнение (10)

называется мажорантой Штурма [5] для уравнения (9).

Теорема 1.  Пусть коэффициенты уравнений (9) и (10) непрерывны на   и пусть уравнение  является мажорантой Штурма уравнения (9). Предположим, что  и  являются решениями уравнений  (9) и  соответственно, всюду на отрезке   удовлетворяют соотношениям:

,   ,                                 (11)

и в точке  выполнено неравенство

.                                                         (12)

Тогда всюду на 

                                                      (13)

где  

Доказательство  этой теоремы приводится в [1].

Пусть  – решение задачи

Применив к задачам  (6) и (14) теорему 1, получаем оценку

 ,

Для решения задачи (7) имеет место оценка

 ,                        

Пусть  – решение задачи

Применяя на отрезке  тождество Лагранжа к задачам (6) и (17), получаем оценку

Для решения задачи (7) имеет место оценка

Теорема 2.  Пусть

всюду на . Тогда для решения задачи  имеет место  оценка

Доказательство. Воспользуемся представлением решения задачи  с помощью функции Грина:

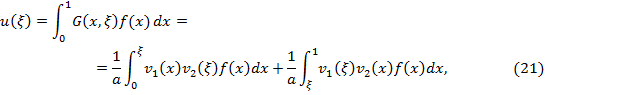
где  и решения задач (6) и (7), а постоянная  вычисляется по формуле (8).

Из (21) получаем с учетом оценок (15), (16), (18), (19): 

Теорема доказана.

Правая часть неравенства  примет наибольшее значение при  . Следовательно, для всех  имеет место оценка

откуда для задачи следует априорная оценка

 

Рецензенты:  

Шхануков-Лафишев М.Х.,  д.ф.-м.н., профессор,ФГБУН Институт информатики и проблем регионального управления   Кабардино-Балкарского   научного центра РАН г. Нальчик;

Ашабоков Б.А. д.ф.-м.н., профессорВысокогорного Геофизического Институт, г. Нальчик.