Полиномиальным решениям дифференциальных уравнений посвящено немало работ (например, [1,2,4,5]). Вместе с тем исследования, посвященные доказательству разрешимости дифференциальных уравнений с отклоняющимся аргументом таким методом, практически отсутствуют. Тем более остаются мало исследованы вырождающиеся уравнения с отклоняющимся аргументом, которые возникают при редукции вопросов разрешимости уравнений в частых производных к вопросу разрешимости, соответствующих обыкновенных дифференциальных уравнений [3,6,7].
В настоящей работе предложено полиномиальное решение для модельного неоднородного вырождающегося дифференциального уравнения второго порядка с отклоняющимся аргументом нейтрального типа.
Цель исследования
Доказать разрешимость двухточечной краевой задачи для дифференциального уравнения с отклоняющимся аргументом методом посредством построения полиномиального решения.
Постановка задачи. На отрезке ![]() рассмотрим уравнение
рассмотрим уравнение
![]() (1)
(1)
где ![]() причем
причем ![]()
Для уравнения (1) исследуем следующую задачу.
Задача 1. Найти регулярное решение уравнения (1), удовлетворяющее условиям:
![]() (2)
(2)
где ![]()
Доказательство разрешимости. Решение задачи 1 будем искать в виде
![]() (3)
(3)
где ![]()
Подставляя (3) в (1), получим:
![]() (4)
(4)
Отсюда при ![]() находим:
находим:
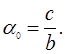 (5)
(5)
Для определения коэффициентов ![]() положим в (4)
положим в (4) ![]() а затем
а затем ![]() . В результате будем иметь:
. В результате будем иметь:
![]()
![]()
или
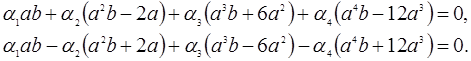 (6)
(6)
С другой стороны, удовлетворяя (3) условиям (2), получим:
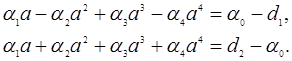 (7)
(7)
Подставляя систему (6), (7) в матричной форме, будем иметь:
![]() (8)
(8)
где
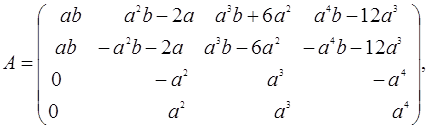
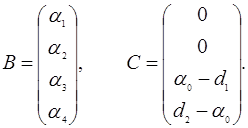
Из (8) очевидно находим:
![]() (9)
(9)
В силу легко устанавливаемого неравенства:
![]()
убеждаемся в том, что задача 1 допускает построение приближенного аналитического решения в виде (3), где ![]() определяются соотношениями (5) и (9).
определяются соотношениями (5) и (9).
Исследование частного случая
В качестве частного случая рассмотрим уравнение (1), когда ![]()
Таким образом, уравнение (1) принимает вид:
![]() (10)
(10)
где ![]() причем
причем ![]()
Для уравнения (10) на интервале ![]() исследуем следующую задачу.
исследуем следующую задачу.
Задача 2. Найти регулярное решение уравнения (10), удовлетворяющее условиям:
![]() (11)
(11)
Решение задачи 2 будем искать описанным выше методом, в виде полинома (3).
Подставляя выбранные значения для с и b в соотношение (5), находим:
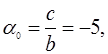 (14)
(14)
Для определения коэффициентов ![]() получаем систему уравнений:
получаем систему уравнений:
![]() (15)
(15)
где
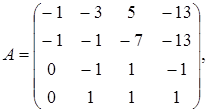
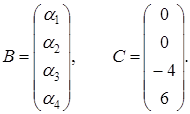
Разрешая (15) относительно столбца неизвестных, будем иметь:
![]() (16)
(16)
Легко убедиться в том, что:
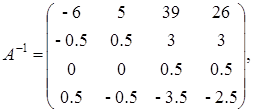
Таким образом, из (16) с учетом (14) получим:
![]() (17)
(17)
На основе соотношения (17) в пакете MathCad были проведены вычислительные эксперименты.
Результаты вычислительного эксперимента, связанного с построением графика функции, определяющей решение задачи 2, представлены на следующем рисунке.
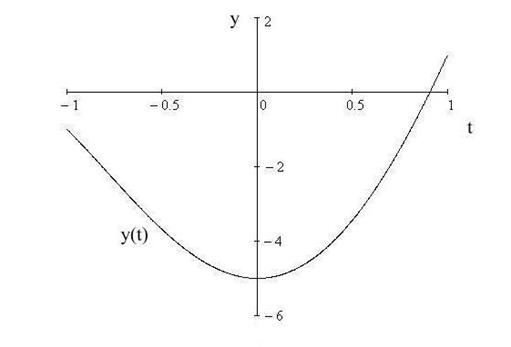
График функции у(t)
Расчеты показывают, что полученное решение удовлетворяет всем условиям сформулированной задачи.
Заключение
Таким образом, в работе предложен метод построения полиномиального решения задачи 1 в виде (3). Данное решение является приближенным аналитическим решением исходной задачи, принадлежит требуемому классу функций и позволяет провести численный анализ с визуализацией решения практически без временных затрат.
Рецензенты:
Журтов А.Х., д.ф.-м.н., профессор, заведующий кафедрой геометрии и высшей алгебры Кабардино-Балкарского государственного университета, г. Нальчик;
Хаширова Т.Ю., д.т.н., профессор, заведующий кафедрой САКТУ Кабардино-Балкарского государственного университета, г. Нальчик.
Библиографическая ссылка
Лесев В.Н., Шарданова М.А. КРАЕВАЯ ЗАДАЧА ДЛЯ ВЫРОЖДАЮЩЕГОСЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22411 (дата обращения: 28.02.2026).



