В настоящее время дизельные электростанции (ДЭС) широко используются в качестве источников основного, резервного или аварийного энергоснабжения различных объектов. Они также подходят для генерации мобильного питания и широко применяются на железных дорогах, подводных лодках и кораблях. Дизельный двигатель, который используется в качестве первичного двигателя для генерирования электрической энергии, является одним из основных компонентов в ДЭС.
Методы математического моделирования и оптимизации широко используются для исследований, направленных на улучшение энергетической и экономической эффективности дизельных электростанций. Актуальность таких исследований увеличивается с возрастающими требованиями экономичности производства электроэнергии и с ужесточением нормативов, ограничивающих выбросы токсинов [2, 3].
В статье описывается алгоритм моделирования дизельного двигателя с переменной скоростью вращения для повышения его энергетической эффективности. Для моделирования рабочих характеристик двигателя внутреннего сгорания применено построение функциональной модели средствами Model-Based Calibration Toolbox™ (MBC Toolbox) с последующим экспортом в среду Simulink (MATLAB). Аппроксимирующая функция имитирует мощность (P) как функцию двух аргументов: скорости вращения вала (n) и абсолютного расхода топлива (g). Программная среда MatLab предлагает много возможностей для создания и проверки модели на адекватность. Пакет MBC Toolbox предназначен для проектирования экспериментов и статистических моделей и калибровки сложных систем. Особенностью процесса калибровки в MBC Toolbox™ является то, что полученный результат – это откалиброванная формула оценки процесса, или функция, предназначенная для подсистем контроля в электронных управляющих устройствах [1, 5]. Кроме того, в процессе моделирования могут быть сглажены ошибки входных данных. В MBC Toolbox используются три вида стратегий: одноуровневые (one-stage), двухуровневые (two-stage) и точечные (point-by-point). В работе рассматривается одноуровневая стратегия, которая предназначена для выявления и разработки отношения между переменными в сложных системах с несколькими переменными. Использование инструментальных средств разработки экспериментов и статистических моделей обусловлено тем, что экспериментальное определение характеристик двигателя внутреннего сгорания требует существенных затрат, и эти характеристики не являются обязательными при разработке новых двигателей, поэтому их определение не входит в планы разработчиков и производителей.
Алгоритм моделирования дизельного двигателя
1. Выбор модели
В качестве исходных данных моделирования использованы характеристики дизельного двигателя KM2V80 (табл. 1) [4]. Так как целью исследования не является изменение конструктивного исполнения дизельного двигателя, он может быть представлен в виде простой функциональной модели по типу «черного ящика».
Таблица 1
Экспериментальные данные дизеля KM2V80
|
P, кВт |
n, об/мин |
g, г/кВт∙ч |
P, кВт |
n, об/мин |
g, г/кВт∙ч |
P, кВт |
n, об/мин |
g, г/кВт∙ч |
|
2,861 |
3260,4 |
457,241 |
2,856 |
2553 |
350,867 |
7,698 |
1901,4 |
212,187 |
|
3,404 |
3250,2 |
406,949 |
3,370 |
2552,4 |
327,563 |
8,022 |
1888,2 |
214,786 |
|
4,548 |
3239,4 |
355,043 |
4,416 |
2529 |
293,501 |
2,660 |
1775,4 |
227,490 |
|
6,443 |
3196,8 |
304,564 |
5,922 |
2491,2 |
266,584 |
3,493 |
1745,4 |
221,638 |
|
7,642 |
3178,8 |
280,121 |
7,277 |
2470,8 |
248,925 |
4,126 |
1722 |
220,201 |
|
9,713 |
3150,6 |
255,215 |
9,058 |
2437,8 |
231,09 |
4,676 |
1706,4 |
221,333 |
|
9,985 |
3140,4 |
254,975 |
12,054 |
2408,4 |
215,077 |
5,279 |
1674 |
222,092 |
|
12,282 |
3114,6 |
225,564 |
12,675 |
2392,2 |
218,586 |
6,095 |
1651,2 |
210,752 |
|
2,856 |
3038,4 |
398,97 |
2,852 |
2299,8 |
296,656 |
6,665 |
1639,8 |
211,981 |
|
3,384 |
3034,2 |
367,852 |
3,351 |
2292,6 |
282,007 |
7,022 |
1625,4 |
214,049 |
|
4,439 |
3006,6 |
329,802 |
4,343 |
2266,2 |
262,374 |
2,589 |
1527 |
186,5864 |
|
6,125 |
2968,8 |
290,149 |
5,738 |
2239,8 |
242,600 |
3,184 |
1497 |
204,932 |
|
7,454 |
2951,4 |
266,964 |
6,750 |
2221,2 |
228,751 |
3,993 |
1450,8 |
206,914 |
|
9,611 |
2921,4 |
245,015 |
7,979 |
2191,2 |
217,280 |
4,892 |
1384,8 |
204,122 |
|
12,967 |
2875,2 |
220,124 |
9,490 |
2158,2 |
214,220 |
5,542 |
1348,2 |
205,603 |
|
2,852 |
2818,8 |
375,283 |
10,085 |
2142 |
212,276 |
2,51587 |
1260 |
148,580 |
|
3,383 |
2793 |
345,177 |
2,760 |
2037,6 |
250,263 |
2,885 |
1219,8 |
168,560 |
|
4,399 |
2763 |
316,450 |
3,151 |
2020,8 |
241,056 |
3,374 |
1177,8 |
182,052 |
|
5,960 |
2734,8 |
278,890 |
3,844 |
2001,6 |
238,675 |
3,886 |
1131 |
188,858 |
|
7,369 |
2712 |
259,103 |
4,818 |
1977,6 |
230,888 |
4,212 |
1079,4 |
196,173 |
|
9,294 |
2683,8 |
237,551 |
5,560 |
1960,2 |
221,917 |
|
|
|
|
12,020 |
2638,2 |
221,798 |
6,499 |
1934,4 |
220,701 |
|
|
|
Функциональная модель (кибернетическая) – это математическая модель, устанавливающая взаимно однозначное соответствие между входными и выходным воздействиями объекта (системы) без отображения происходящих внутри процессов. Функциональные модели просты по структуре, строятся экспериментальными методами и позволяют получить достоверные результаты при минимальных временных и экономических затратах.
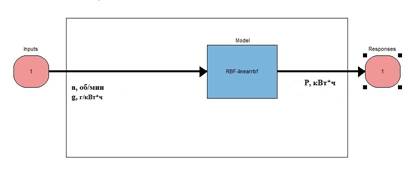
Функциональная модель дизеля формируется по его фактической нагрузочно-скоростной характеристике, которая устанавливает зависимость его эффективной мощности P от скорости вращения вала n и абсолютного расхода топлива g (рис. 1).
|
|
Рис. 1. Процесс создания модели
Для создания оптимальной математической модели использован одноступенчатый план проведения испытаний и интерполяция радиальной базисной функцией (Radial Basic Function). Радиальная базисная функция (RBF) имеет вид:
![]() ,
,
где х и хс – это n-мерные векторы, ||.|| обозначает евклидову норму. Вектор xc называется центром радиальной базисной функции. В MBC Toolbox используется линейная комбинация N радиальных базисных функций с N различными центрами:
![]() ,
,
где ![]() – вес, соответствующий радиальной базисной функции
– вес, соответствующий радиальной базисной функции ![]() с центром xi. Различные типы RBF представлены в таблице 2.
с центром xi. Различные типы RBF представлены в таблице 2.
Таблица 2
Виды RBF-функций
|
Название |
Формула |
|
линейная |
|
|
Гауссиан |
|
|
мультиквадрик |
|
|
обратный мультиквадрик |
|
|
Функции Вендланда с компактным носителем |
|
|
кубическая |
|
В процессе моделирования необходимо задать четыре параметра RBF-функции: вес, центры, ширину и ![]() . Каждый из них может оказывать значительное влияние на качество результата. Опции View Model, Stepwise и View Centers используются для установки ширины, веса и центров (рис. 2) соответственно. Начальное значение
. Каждый из них может оказывать значительное влияние на качество результата. Опции View Model, Stepwise и View Centers используются для установки ширины, веса и центров (рис. 2) соответственно. Начальное значение ![]() выбирается между –3 и 3.
выбирается между –3 и 3.
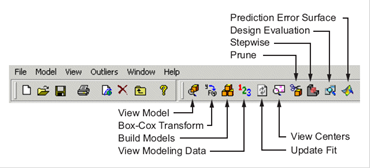
Рис. 2. Панель инструментов MBC Toolbox
2. Калибровка модели
Качество модели оценивается достоверностью и статистическими характеристиками результатов, полученных в процессе проведения модельных экспериментов.
Опция Stepwise предлагает несколько алгоритмов, таких как Minimize Press, Forward Selection, Backwards Selection и Prune, для уточнения модели и удаления менее полезных элементов (терм). Алгоритм Minimize Press позволяет минимизировать прогнозируемую сумму квадратов ошибок (PRESS). На каждом шаге можно наблюдать, как удаление или добавление элементов влияет на PRESS-статистику. Эта статистика является мерой прогнозируемого качества модели. Поскольку программа предлагает несколько моделей с близкими по значению PRESS-статистики, то возникает необходимость использования дополнительных критериев отбора для выбранных моделей. Forward Selection добавляет все элементы, которые являются статистически значимыми для данной модели. Backwards Selection, напротив, удаляет все статистически не значимые элементы модели. Prune является альтернативным алгоритмом, нацеленным на улучшение качества модели; в отличие от вышеописанных алгоритмов он удаляет и добавляет элементы в заданном порядке. При этом в первую очередь выбираются наиболее важные элементы для улучшения качества модели.
Следующим этапом улучшения качества модели является применение преобразования Box-Cox Transform. Это преобразование приводит экспериментальные данные к нормальному закону распределения. Для последовательности данных ![]() ,
, ![]() , …,
, …, ![]() преобразование Box-Cox определяется формулой:
преобразование Box-Cox определяется формулой:
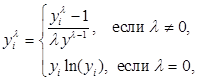
где ![]() – параметр, минимизирующий значение суммы квадратов ошибок (SSE) и подобранный по методу максимального правдоподобия. На рисунке 3 показан график зависимости SSE от параметра
– параметр, минимизирующий значение суммы квадратов ошибок (SSE) и подобранный по методу максимального правдоподобия. На рисунке 3 показан график зависимости SSE от параметра ![]() . По умолчанию параметр
. По умолчанию параметр ![]() принимает значение от -3 до 3 с шагом 0,5. Зеленая точка соответствует минимальному значению SSE(λ). Красной линией показан 95%-ный доверительный интервал для
принимает значение от -3 до 3 с шагом 0,5. Зеленая точка соответствует минимальному значению SSE(λ). Красной линией показан 95%-ный доверительный интервал для ![]() . В качестве текущего значения
. В качестве текущего значения ![]() (красная точка) следует выбирать ближайшее значение к минимуму SSE из доверительного интервала.
(красная точка) следует выбирать ближайшее значение к минимуму SSE из доверительного интервала.
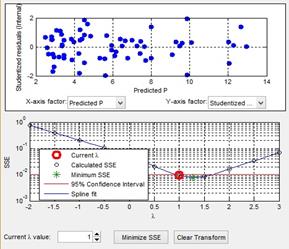
Рис. 3. Окно преобразования Box-Cox
3. Оценка погрешности
При построении линейных моделей и моделей с использованием RBF-функций доступна опция Prediction Error Variance Viewer, предназначенная для исследования прогнозной способности модели. Prediction Error Variance (PEV) – прогнозируемая дисперсия ошибок – является мерой точности модельных прогнозов. PEV может использоваться для проверки как расчетов, так и моделей.
Таким образом, точность модельных прогнозов зависит от расчета PEV и среднеквадратической ошибки данных. Необходимо попытаться сделать PEV для расчетов настолько низкой, насколько это возможно. Низкое значение (близкое к нулю) означает, что получен хороший прогноз для рассматриваемой точки. Если в результате расчета получается PEV < 1, тогда ошибки сокращены в процессе настройки модели. Если же получается PEV > 1, это означает, что любые ошибки в измерениях накапливаются. На рисунке 4 показан 3-D график поверхности ошибок PEV.
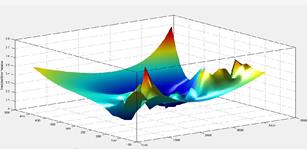
Рис. 4. Поверхность ошибок
После построения моделей программа автоматически составляет список лучших моделей. С учетом этого принята модель RBF-linearrbf-29, выбор которой основан на следующих критериях отбора: PRESS RMSE, RMSE, Box-Cox (рис. 5).
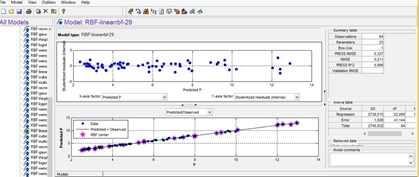
Рис. 5. Модель RBF-linearrbf-29
Нижний график, изображенный на рисунке 5, называется Predicted/Observed (Расчетный/Экспериментальный), он дает наглядное представление о точности «подгонки» исходных данных к выбранному шаблону модели в зависимости от входной переменной величины (g). Данное представление подтверждает адекватность принятой модели.
4. Заключение
В ходе моделирования рассмотрены различные методы интерполяции и аппроксимации экспериментальных данных. Окончательная модель выбрана на основе оценки моделирования ошибки с выбором различных критериев оптимизации. Компьютерная модель дизельного двигателя, полученная в результате экспорта выбранной функции в Simulink, позволяет исследовать режимы работы на основе экспериментальных данных. Результаты адекватности выбора модели представлены в таблице 3.
Таблица 3
Выборочные исходные данные и результаты в среде Simulink
|
Исходные данные |
Данные, полученные в среде Simulink |
|||
|
n, об/мин |
g, г/кВт∙ч |
P, кВт |
P, кВт |
PEV |
|
3260,4 |
457,2413 |
2,86 |
2,799 |
0,0329 |
|
3250,2 |
406,9499 |
3,40 |
3,437 |
0,0086 |
|
3038,4 |
398,97 |
2,85 |
2,94 |
0,006 |
|
2818,8 |
375,2836 |
2,85 |
2,84 |
0,0037 |
|
3034,2 |
367,8528 |
3,38 |
3,48 |
0,0067 |
|
3239,4 |
355,0439 |
4,54 |
4,37 |
0,019 |
|
2553 |
350,8672 |
2,86 |
2,706 |
0,0029 |
|
2793 |
345,1776 |
3,38 |
3,436 |
0,003 |
|
3006,6 |
329,8022 |
4,44 |
4,566 |
0,0049 |
|
2552,4 |
327,5636 |
3,37 |
3,23 |
0,0028 |
|
2763 |
316,450 |
4,4 |
4,258 |
0,003 |
|
3196,8 |
304,564 |
6,44 |
6,477 |
0,005 |
|
2299,8 |
296,656 |
2,85 |
3,177 |
0,004 |
|
2529 |
293,501 |
4,42 |
4,366 |
0,003 |
|
2968,8 |
290,149 |
6,13 |
6,172 |
0,007 |
|
2292,6 |
282,007 |
3,35 |
3,653 |
0,004 |
|
3178,8 |
280,121 |
7,64 |
7,913 |
0,005 |
|
2734,8 |
278,890 |
5,96 |
5,99 |
0,005 |
|
2951,4 |
266,964 |
7,45 |
7,372 |
0,017 |
Отличительной особенностью этого метода моделирования является возможность изучать широкий спектр условий эксплуатации с минимальной погрешностью, не превышающей одного процента по отношению к экспериментальным данным.
Рецензенты:
Литвак В.В., д.т.н., профессор, профессор кафедры «Атомные и тепловые электростанции», Национальный исследовательский Томский политехнический университет, г. Томск;
Кабышев А.В., д.ф.-м.н., профессор кафедры «Электроснабжение промышленных предприятий», Энергетический институт, Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Сарсикеев Е.Ж., Молдованова Е.А., Шолохова И.И., Сарсикеев Е.Ж., Молдованова Е.А. ПРИМЕНЕНИЕ MATLAB MBC TOOLBOX ДЛЯ СОЗДАНИЯ МОДЕЛЕЙ ХАРАКТЕРИСТИК ДИЗЕЛЬНОГО ДВИГАТЕЛЯ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22276 (дата обращения: 11.02.2026).