В работе проводится исследование краевой задачи со свободными границами, описывающей динамику температурного поля при деструкции тканей плоскопараллельными аппликаторами. Рассмотрена задача гипотермии, когда отсутствует замороженная область и, следовательно, определению подлежат только функции ![]() и свободная граница
и свободная граница ![]() . Для решения задачи в работе применяются методы нелинейных интегральных, интегро-дифференциальных уравнений, метод Ротэ, метод эквивалентной линеаризации, а также проведена конечномерная аппроксимация [4, 3].
. Для решения задачи в работе применяются методы нелинейных интегральных, интегро-дифференциальных уравнений, метод Ротэ, метод эквивалентной линеаризации, а также проведена конечномерная аппроксимация [4, 3].
Получено точное аналитическое решение соответствующей стационарной задачи, которое определяет очень важные для хирурга максимальные размеры замораживания, криопоражения и теплового возмущения.
Конечномерной аппроксимацией решение полученной системы сведено к решению системы нелинейных алгебраических уравнений.
Постановка задачи
В различных областях медицины при деструкции тканей применяются достаточно протяженные плоские аппликаторы. Определение динамики температурного поля в этом случае сводится к решению следующей задачи со свободными границами для нелинейных эволюционных уравнений [6, 5]:
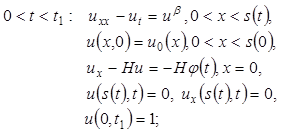 (1)
(1)
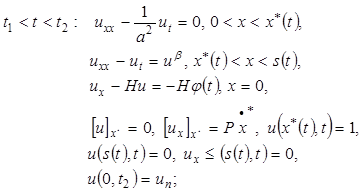 (2)
(2)
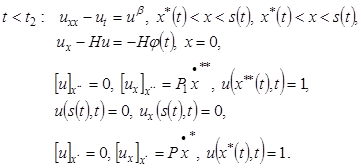 (3)
(3)
В задаче (1)-(3) искомыми являются температурное поле ![]() и границы
и границы ![]() остальные параметры и функции известные,
остальные параметры и функции известные, ![]() .
.
Аналитическое решение соответствующей стационарной задачи (1)–(3) имеет вид:
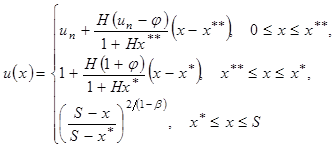 (4)
(4)
где
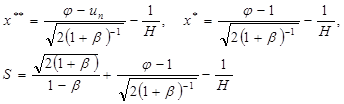 (5)
(5)
Задача гипотермии биологической ткани
Динамика охлаждения описывается решением задачи со свободной границей [1]:
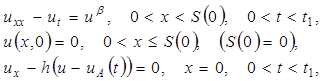 (6)
(6)
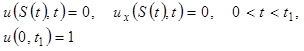
Аналитическое решение соответствующей стационарной задачи (6) имеет вид:
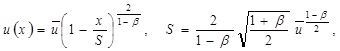 (7)
(7)
где ![]() — положительный корень уравнения
— положительный корень уравнения
 (8)
(8)
При ![]() , вводя сетку
, вводя сетку ![]() с достаточно малым шагом
с достаточно малым шагом ![]() и заменяя, оператор
и заменяя, оператор ![]() конечно-разностным аналогом, для определения приближенного значения
конечно-разностным аналогом, для определения приближенного значения ![]() и
и ![]() функций
функций ![]() в точках
в точках ![]() получаем следующую аппроксимацию краевой задачи (6) в виде системы краевых задач для обыкновенных дифференциальных уравнений:
получаем следующую аппроксимацию краевой задачи (6) в виде системы краевых задач для обыкновенных дифференциальных уравнений:
![]()
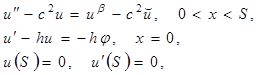 (9)
(9)
где индекс ![]() опущен, а знак
опущен, а знак ![]() означает значения соответствующих величин на
означает значения соответствующих величин на ![]() -м временном слое;
-м временном слое; ![]() .
.
С помощью функции Грина и формулы Грина на каждом временном слое осуществлено их сведение к нелинейному интегральному уравнению Вольтерра [1, 3]:
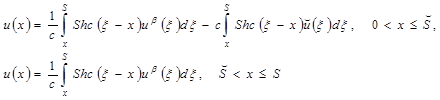 (10)
(10)
и уравнению
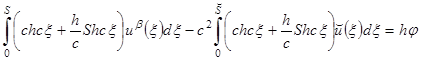 (11)
(11)
где ![]() и
и ![]() — значения на данном, а
— значения на данном, а ![]() и
и ![]() — на предыдущем временных слоях.
— на предыдущем временных слоях.
Вводя равномерную сетку ![]() и заменяя входящие в (10), (11) интегралы приближенными выражениями
и заменяя входящие в (10), (11) интегралы приближенными выражениями
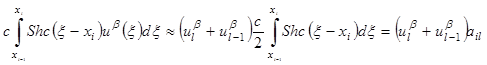 (12)
(12)
приходим к системе нелинейных уравнений относительно узловых значений ![]() и числа
и числа ![]() :
:
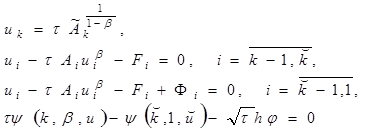 (13)
(13)
где
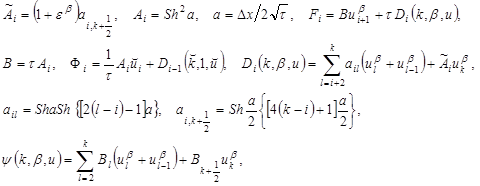
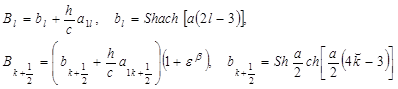
При ![]() получаем:
получаем:
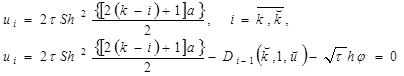 (14)
(14)
Простейшие приближенные решения системы (10), (11) можно получить полагая
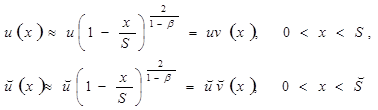 (15)
(15)
Для ![]() и
и ![]() при этом получаем систему нелинейных уравнений
при этом получаем систему нелинейных уравнений
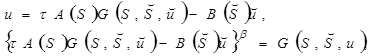 (16)
(16)
где
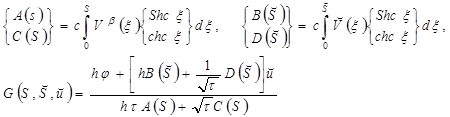 (17)
(17)
Считая, что ![]() , и воспользовавшись приближениями вида (12), приходим к задаче определения
, и воспользовавшись приближениями вида (12), приходим к задаче определения ![]() по
по ![]() и
и ![]() из условия перемены знака следующей функции целочисленного аргумента:
из условия перемены знака следующей функции целочисленного аргумента:
![]() (18)
(18)
где
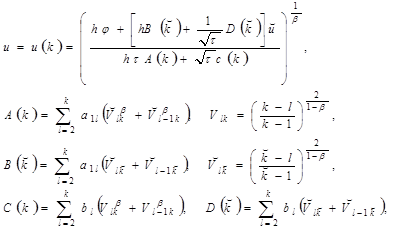 (19)
(19)
При ![]() интегралы (17) вычисляются и мы получаем:
интегралы (17) вычисляются и мы получаем:
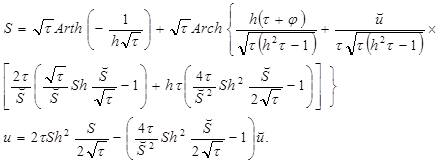 (20)
(20)
Если к тому же ![]() , то
, то 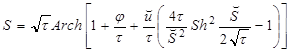 .
.
Приближенное решение можно искать в виде [1]:
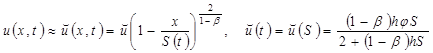 . (21)
. (21)
Краевые условия выполняются для любой функции ![]() . Потребуем, чтобы конструкция (21) удовлетворяла дифференциальному уравнению в смысле равенства нулю интегральной невязки.
. Потребуем, чтобы конструкция (21) удовлетворяла дифференциальному уравнению в смысле равенства нулю интегральной невязки.
В результате приходим к задаче Коши для определения ![]()
![]() . (22)
. (22)
Заменяя производную ![]() конечной разностью, получаем нелинейное уравнение для значения
конечной разностью, получаем нелинейное уравнение для значения ![]() на данном временном слое:
на данном временном слое:
![]() . (23)
. (23)
Численные расчеты показывают, что вполне удовлетворительные результаты дают простейшие приближенные решения.
Рецензенты:
Шхануков-Лафишев М.Х., д.ф.-м.н., профессор, ФГБУН «Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН», г. Нальчик;
Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного Геофизического Института, г. Нальчик.
Библиографическая ссылка
Кайгермазов А.А., Кудаева Ф.Х., Кармоков М.М., Нахушева Ф.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПЛОСКОЙ КРИОДЕСТРУКЦИИ БИОЛОГИЧЕСКОЙ ТКАНИ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=21683 (дата обращения: 11.02.2026).



