Введение
Электродиализный аппарат имеет периодическую структуру, состоящую из чередующих камер обессоливания и концентрирования, а также двух электродных камер. Изменение концентрации в камере концентрирования можно учесть в граничных условиях. Таким образом, основной задачей является моделирование переноса в камере обессоливания. Пусть ![]() соответствует условной межфазной границе анионообменная мембрана/раствор,
соответствует условной межфазной границе анионообменная мембрана/раствор, ![]() соответствует условной межфазной границе катионообменная мембрана/раствор,
соответствует условной межфазной границе катионообменная мембрана/раствор, ![]() – входу, а
– входу, а ![]() – выходу из камеры обессоливания,
– выходу из камеры обессоливания, ![]() – заданная скорость прокачивания раствора. Будем считать, что скорость течения раствора имеет форму параболы Пуазейля или моделируется по-другому.
– заданная скорость прокачивания раствора. Будем считать, что скорость течения раствора имеет форму параболы Пуазейля или моделируется по-другому.
Для математического моделирования явлений переноса для бинарного электролита в камере обессоливания используется краевая задача для системы уравнений Нернста – Планка и Пуассона [4], которая достаточно сложна для аналитического и численного решения.
2. Постановка задачи. Нами в работе [5], для 1:1 электролита с одинаковыми коэффициентами диффузии катионов и анионов, была выведена упрощенная модельная задача с функцией Хэвисайда [1] и показано, что она достаточна адекватна. В данной работе предлагается асимптотическое решение соответствующей краевой задачи, которая имеет безразмерный вид [1, 2]:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() ,
, ![]()
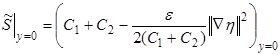 ,
, 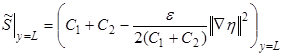 (4)
(4)
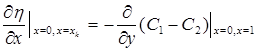 ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , (5)
, (5)
где ![]() – искомая напряженность,
– искомая напряженность, ![]() ,
,![]() – концентрации катионов и анионов,
– концентрации катионов и анионов, ![]() – обобщенная общая «концентрация»,
– обобщенная общая «концентрация», ![]() – плотность тока,
– плотность тока, ![]() – функция тока для плотности тока
– функция тока для плотности тока ![]() , т.е.
, т.е. ![]() ,
, ![]() ,
, ![]() – безразмерный малый параметр, равный удвоенному квадрату отношения Дебаевской длины к ширине канала,
– безразмерный малый параметр, равный удвоенному квадрату отношения Дебаевской длины к ширине канала, ![]() ,
, ![]() – число Пекле,
– число Пекле, ![]() – заданная скорость протока электролита в камере обессоливания,
– заданная скорость протока электролита в камере обессоливания, ![]() – функция Хэвисайда,
– функция Хэвисайда, ![]() – ток в цепи,
– ток в цепи, ![]() – длина канала,
– длина канала, ![]() – кососимметрическое скалярное произведение.
– кососимметрическое скалярное произведение.
При запредельных режимах функция ![]() меняет знак в области
меняет знак в области ![]() по крайней мере, для небольших
по крайней мере, для небольших ![]() , причем дважды. Из этого следует, что функция
, причем дважды. Из этого следует, что функция ![]() имеет в разных частях области различные асимптотические представления.
имеет в разных частях области различные асимптотические представления.
Нами показано, что область ![]() , где значение функции
, где значение функции ![]() положительно является областью электронейтральности, а отрицательно
положительно является областью электронейтральности, а отрицательно ![]() – пространственного заряда.
– пространственного заряда.
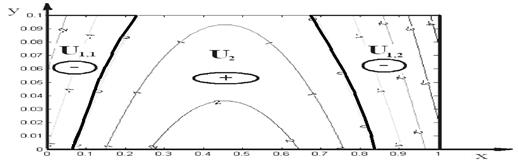
Рисунок 1. Область знакопостоянства функции ![]()
Особенностью задачи является то, что функция ![]() из уравнения (1) находится независимо от функций
из уравнения (1) находится независимо от функций ![]() и
и ![]() .
.
3. Асимптотическое решение в области электронейтральности
3. 1. Асимптотическое разложение
Используем в области электронейтральности (![]() ) для асимптотического решения следующие разложения:
) для асимптотического решения следующие разложения:
![]() ,
, ![]() .
.
Подставляя данные разложения в систему уравнений и приравнивая коэффициенты при равных степенях ![]() , получим уравнения, решая которые можно найти все коэффициенты разложения. Для нахождения решения
, получим уравнения, решая которые можно найти все коэффициенты разложения. Для нахождения решения ![]() -го приближения получаем следующую систему уравнений:
-го приближения получаем следующую систему уравнений:
![]() (6)
(6)
![]() (7)
(7)
где
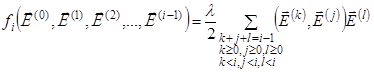
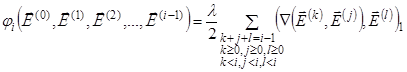
3. 2. Алгоритм решения начального и первого приближения
Для начального приближения имеем систему уравнений:
![]() ,
,
![]() ,
,
которая после ряда преобразований принимает вид:
![]() (8)
(8)
![]() (9)
(9)
Из системы уравнений (9)–(10) видно, что вначале из уравнения (9) находится решение ![]() , далее, используя условие
, далее, используя условие 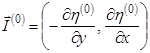 , вычисляем
, вычисляем ![]() , затем находим
, затем находим ![]() .
.
Для приближения первого порядка получаем систему уравнений:
![]()
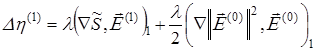 ,
,
которая после некоторых преобразований преобразуется к виду:
![]() (10)
(10)
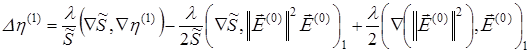 (11)
(11)
Из системы уравнений (10)–(11) видно, что первое приближение находится по такому же алгоритму, что и начальное приближение.
4. Асимптотическое решение в области пространственного заряда
4. 1. Асимптотическое разложение
Сделаем замену: ![]() , и используем в области пространственного заряда (
, и используем в области пространственного заряда (![]() ) для асимптотического решения следующие разложения тогда
) для асимптотического решения следующие разложения тогда
![]() ,
,
![]() ,
,
тогда для ![]() -го приближения имеем систему уравнений
-го приближения имеем систему уравнений
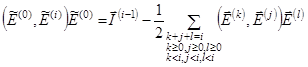 (12)
(12)
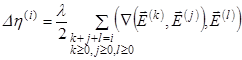 (13)
(13)
Система уравнений (12) может быть записана в виде:
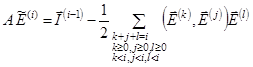 ,
,
где  .
.
Заметим, что для ![]() получаем систему линейных уравнений с нулевым определителем
получаем систему линейных уравнений с нулевым определителем ![]() . Для однозначного определения
. Для однозначного определения ![]() - го приближения используется условие разрешимости
- го приближения используется условие разрешимости ![]() - го приближения, которое имеет вид
- го приближения, которое имеет вид
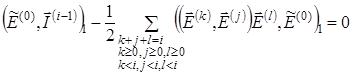 (14)
(14)
4. 2. Алгоритм решения начального и первого приближения
Система уравнений для нулевого приближения имеет вид
![]() (15)
(15)
![]() (16)
(16)
Система уравнений для первого приближения имеет вид
![]() (17)
(17)
![]() (18)
(18)
Система уравнений для второго приближения для ![]() имеет вид:
имеет вид:
![]() (19)
(19)
Уравнение (15) можно записать в виде
![]() (20)
(20)
Из этого уравнения не удается однозначно найти ![]() и
и ![]() , поэтому необходимо использовать условие разрешимости уравнения для
, поэтому необходимо использовать условие разрешимости уравнения для ![]() , которое, как следует из (14), имеет следующий вид:
, которое, как следует из (14), имеет следующий вид:
![]() (21)
(21)
Решая систему уравнений (20) и (21), получаем однозначное выражение ![]() через
через ![]() :
:
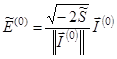 , (22)
, (22)
с учетом которого уравнение (18) преобразуется к виду:
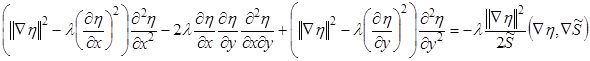 (23)
(23)
Уравнение (23) является квазилинейным уравнением параболического типа.
Из уравнения (19) имеем следующее условие разрешимости для первого приближения
![]() (24)
(24)
Решая систему уравнений (21) и (24), выражаем напряженность электрического поля через плотность тока для первого приближения
![]() , (25)
, (25)
где 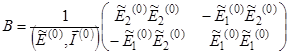 ,
, 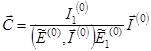 .
.
Из уравнений (18) и (19) можно получить выражение для нахождения ![]() :
:
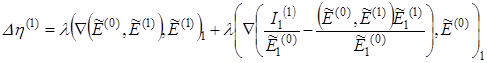 ,
,
в которое из (21) подставляем ![]() и получаем уравнение для
и получаем уравнение для ![]() . Соответствующее уравнение не приводится из-за ее громоздкости.
. Соответствующее уравнение не приводится из-за ее громоздкости.
5. Алгоритм численного решения начального приближения
Для численного решения вводится в рассмотрение дифференциальный оператор ![]() , который определяется следующим образом [3]:
, который определяется следующим образом [3]:
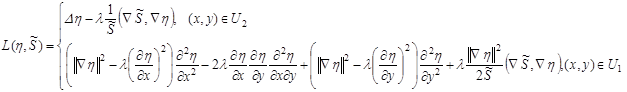 ,
,
Тогда для функций ![]() и
и ![]() получается система уравнений
получается система уравнений
![]() (26)
(26)
![]() (27)
(27)
с соответствующими краевыми условиями (4)–(5).
Для численного решения использовался метод установления, для дискретизации применялись явная и неявная разностные схемы. На рисунке 2 приведены графики решений краевой задачи для функции обобщенной концентрации ![]() и плотности тока
и плотности тока ![]() .
.
а)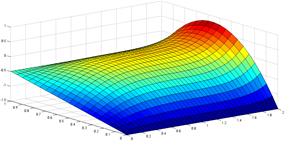 б)
б)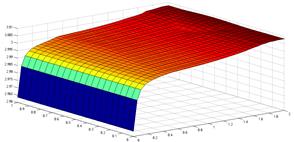
Рисунок 2. Графики решений краевой задачи: а) ![]() , б)
, б) ![]()
Заключение. Краевая задача (11)–(15) относится к классу «жестких» задач [1] из-за наличия малого параметра и поэтому при численном решении при значениях малого параметра ![]() порядка
порядка ![]() требуется шаг дискретизации порядка
требуется шаг дискретизации порядка ![]() , что еще приемлемо по времени решения.
, что еще приемлемо по времени решения.
Однако реально ![]() меняется в пределах от
меняется в пределах от ![]() до
до ![]() . При таких значениях малого параметра численное решение становится затруднительным. Предлагаемое асимптотическое решение позволяет провести численный анализ краевой задачи при произвольно малых значениях параметра
. При таких значениях малого параметра численное решение становится затруднительным. Предлагаемое асимптотическое решение позволяет провести численный анализ краевой задачи при произвольно малых значениях параметра ![]() .
.
Рецензенты:
Осипян Валерий Осипович, д.ф-м.н., доцент, профессор кафедры информационных технологий Кубанского государственного университета, г. Краснодар.
Семенчин Евгений Андреевич, д.ф.-м.н., профессор, заведующий кафедрой высшей алгебры и геометрии Кубанского государственного университета, г. Краснодар.
Криштоп Виктор Владимирович, д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.



