Введение
Электродиализный аппарат имеет периодическую структуру, состоящую из чередующих камер обессоливания и концентрирования, а также двух электродных камер. Изменение концентрации в камере концентрирования можно учесть в граничных условиях. Таким образом, основной задачей является моделирование переноса в камере обессоливания. Пусть ![]() соответствует условной межфазной границе анионообменная мембрана/раствор,
соответствует условной межфазной границе анионообменная мембрана/раствор, ![]() соответствует условной межфазной границе катионообменная мембрана/раствор,
соответствует условной межфазной границе катионообменная мембрана/раствор, ![]() – входу, а
– входу, а ![]() – выходу из камеры обессоливания,
– выходу из камеры обессоливания, ![]() – заданная скорость прокачивания раствора. Будем считать, что скорость течения раствора имеет форму параболы Пуазейля или моделируется по-другому.
– заданная скорость прокачивания раствора. Будем считать, что скорость течения раствора имеет форму параболы Пуазейля или моделируется по-другому.
Для математического моделирования явлений переноса для бинарного электролита в камере обессоливания используется краевая задача для системы уравнений Нернста – Планка и Пуассона [4], которая достаточно сложна для аналитического и численного решения.
2. Постановка задачи. Нами в работе [5], для 1:1 электролита с одинаковыми коэффициентами диффузии катионов и анионов, была выведена упрощенная модельная задача с функцией Хэвисайда [1] и показано, что она достаточна адекватна. В данной работе предлагается асимптотическое решение соответствующей краевой задачи, которая имеет безразмерный вид [1, 2]:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() ,
, ![]()
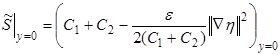 ,
, 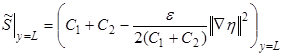 (4)
(4)
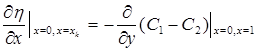 ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , (5)
, (5)
где ![]() – искомая напряженность,
– искомая напряженность, ![]() ,
,![]() – концентрации катионов и анионов,
– концентрации катионов и анионов, ![]() – обобщенная общая «концентрация»,
– обобщенная общая «концентрация», ![]() – плотность тока,
– плотность тока, ![]() – функция тока для плотности тока
– функция тока для плотности тока ![]() , т.е.
, т.е. ![]() ,
, ![]() ,
, ![]() – безразмерный малый параметр, равный удвоенному квадрату отношения Дебаевской длины к ширине канала,
– безразмерный малый параметр, равный удвоенному квадрату отношения Дебаевской длины к ширине канала, ![]() ,
, ![]() – число Пекле,
– число Пекле, ![]() – заданная скорость протока электролита в камере обессоливания,
– заданная скорость протока электролита в камере обессоливания, ![]() – функция Хэвисайда,
– функция Хэвисайда, ![]() – ток в цепи,
– ток в цепи, ![]() – длина канала,
– длина канала, ![]() – кососимметрическое скалярное произведение.
– кососимметрическое скалярное произведение.
При запредельных режимах функция ![]() меняет знак в области
меняет знак в области ![]() по крайней мере, для небольших
по крайней мере, для небольших ![]() , причем дважды. Из этого следует, что функция
, причем дважды. Из этого следует, что функция ![]() имеет в разных частях области различные асимптотические представления.
имеет в разных частях области различные асимптотические представления.
Нами показано, что область ![]() , где значение функции
, где значение функции ![]() положительно является областью электронейтральности, а отрицательно
положительно является областью электронейтральности, а отрицательно ![]() – пространственного заряда.
– пространственного заряда.
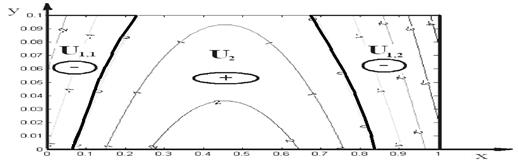
Рисунок 1. Область знакопостоянства функции ![]()
Особенностью задачи является то, что функция ![]() из уравнения (1) находится независимо от функций
из уравнения (1) находится независимо от функций ![]() и
и ![]() .
.
3. Асимптотическое решение в области электронейтральности
3. 1. Асимптотическое разложение
Используем в области электронейтральности (![]() ) для асимптотического решения следующие разложения:
) для асимптотического решения следующие разложения:
![]() ,
, ![]() .
.
Подставляя данные разложения в систему уравнений и приравнивая коэффициенты при равных степенях ![]() , получим уравнения, решая которые можно найти все коэффициенты разложения. Для нахождения решения
, получим уравнения, решая которые можно найти все коэффициенты разложения. Для нахождения решения ![]() -го приближения получаем следующую систему уравнений:
-го приближения получаем следующую систему уравнений:
![]() (6)
(6)
![]() (7)
(7)
где
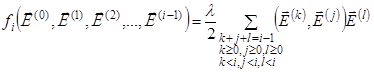
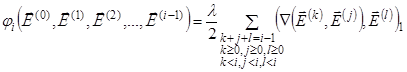
3. 2. Алгоритм решения начального и первого приближения
Для начального приближения имеем систему уравнений:
![]() ,
,
![]() ,
,
которая после ряда преобразований принимает вид:
![]() (8)
(8)
![]() (9)
(9)
Из системы уравнений (9)–(10) видно, что вначале из уравнения (9) находится решение ![]() , далее, используя условие
, далее, используя условие 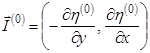 , вычисляем
, вычисляем ![]() , затем находим
, затем находим ![]() .
.
Для приближения первого порядка получаем систему уравнений:
![]()
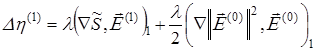 ,
,
которая после некоторых преобразований преобразуется к виду:
![]() (10)
(10)
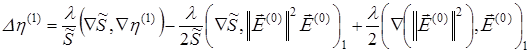 (11)
(11)
Из системы уравнений (10)–(11) видно, что первое приближение находится по такому же алгоритму, что и начальное приближение.
4. Асимптотическое решение в области пространственного заряда
4. 1. Асимптотическое разложение
Сделаем замену: ![]() , и используем в области пространственного заряда (
, и используем в области пространственного заряда (![]() ) для асимптотического решения следующие разложения тогда
) для асимптотического решения следующие разложения тогда
![]() ,
,
![]() ,
,
тогда для ![]() -го приближения имеем систему уравнений
-го приближения имеем систему уравнений
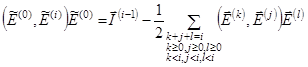 (12)
(12)
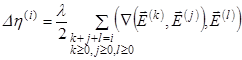 (13)
(13)
Система уравнений (12) может быть записана в виде:
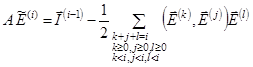 ,
,
где  .
.
Заметим, что для ![]() получаем систему линейных уравнений с нулевым определителем
получаем систему линейных уравнений с нулевым определителем ![]() . Для однозначного определения
. Для однозначного определения ![]() - го приближения используется условие разрешимости
- го приближения используется условие разрешимости ![]() - го приближения, которое имеет вид
- го приближения, которое имеет вид
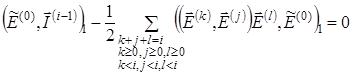 (14)
(14)
4. 2. Алгоритм решения начального и первого приближения
Система уравнений для нулевого приближения имеет вид
![]() (15)
(15)
![]() (16)
(16)
Система уравнений для первого приближения имеет вид
![]() (17)
(17)
![]() (18)
(18)
Система уравнений для второго приближения для ![]() имеет вид:
имеет вид:
![]() (19)
(19)
Уравнение (15) можно записать в виде
![]() (20)
(20)
Из этого уравнения не удается однозначно найти ![]() и
и ![]() , поэтому необходимо использовать условие разрешимости уравнения для
, поэтому необходимо использовать условие разрешимости уравнения для ![]() , которое, как следует из (14), имеет следующий вид:
, которое, как следует из (14), имеет следующий вид:
![]() (21)
(21)
Решая систему уравнений (20) и (21), получаем однозначное выражение ![]() через
через ![]() :
:
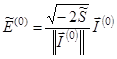 , (22)
, (22)
с учетом которого уравнение (18) преобразуется к виду:
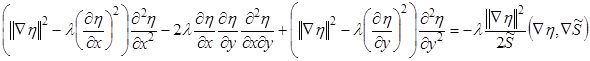 (23)
(23)
Уравнение (23) является квазилинейным уравнением параболического типа.
Из уравнения (19) имеем следующее условие разрешимости для первого приближения
![]() (24)
(24)
Решая систему уравнений (21) и (24), выражаем напряженность электрического поля через плотность тока для первого приближения
![]() , (25)
, (25)
где 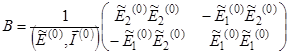 ,
, 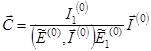 .
.
Из уравнений (18) и (19) можно получить выражение для нахождения ![]() :
:
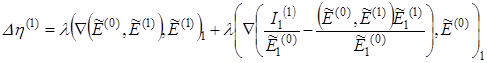 ,
,
в которое из (21) подставляем ![]() и получаем уравнение для
и получаем уравнение для ![]() . Соответствующее уравнение не приводится из-за ее громоздкости.
. Соответствующее уравнение не приводится из-за ее громоздкости.
5. Алгоритм численного решения начального приближения
Для численного решения вводится в рассмотрение дифференциальный оператор ![]() , который определяется следующим образом [3]:
, который определяется следующим образом [3]:
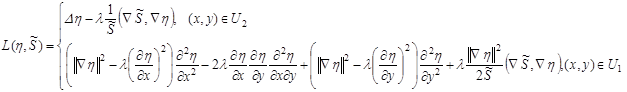 ,
,
Тогда для функций ![]() и
и ![]() получается система уравнений
получается система уравнений
![]() (26)
(26)
![]() (27)
(27)
с соответствующими краевыми условиями (4)–(5).
Для численного решения использовался метод установления, для дискретизации применялись явная и неявная разностные схемы. На рисунке 2 приведены графики решений краевой задачи для функции обобщенной концентрации ![]() и плотности тока
и плотности тока ![]() .
.
а)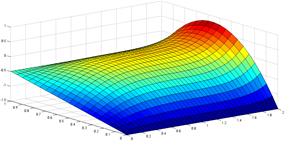 б)
б)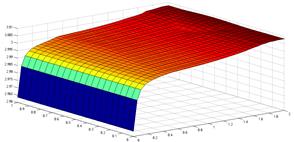
Рисунок 2. Графики решений краевой задачи: а) ![]() , б)
, б) ![]()
Заключение. Краевая задача (11)–(15) относится к классу «жестких» задач [1] из-за наличия малого параметра и поэтому при численном решении при значениях малого параметра ![]() порядка
порядка ![]() требуется шаг дискретизации порядка
требуется шаг дискретизации порядка ![]() , что еще приемлемо по времени решения.
, что еще приемлемо по времени решения.
Однако реально ![]() меняется в пределах от
меняется в пределах от ![]() до
до ![]() . При таких значениях малого параметра численное решение становится затруднительным. Предлагаемое асимптотическое решение позволяет провести численный анализ краевой задачи при произвольно малых значениях параметра
. При таких значениях малого параметра численное решение становится затруднительным. Предлагаемое асимптотическое решение позволяет провести численный анализ краевой задачи при произвольно малых значениях параметра ![]() .
.
Рецензенты:
Осипян Валерий Осипович, д.ф-м.н., доцент, профессор кафедры информационных технологий Кубанского государственного университета, г. Краснодар.
Семенчин Евгений Андреевич, д.ф.-м.н., профессор, заведующий кафедрой высшей алгебры и геометрии Кубанского государственного университета, г. Краснодар.
Криштоп Виктор Владимирович, д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.
Библиографическая ссылка
Хромых А.А., Чубырь Н.О., Коваленко А.В., Уртенов М.Х. НАХОЖДЕНИЕ ВЫСШИХ АСИМПТОТИЧЕСКИХ РАЗЛОЖЕНИЙ КРАЕВОЙ ЗАДАЧИ МОДЕЛИ С ФУНКЦИЕЙ ХЭВИСАЙДА // Современные проблемы науки и образования. 2013. № 4. ;URL: https://science-education.ru/ru/article/view?id=9842 (дата обращения: 13.03.2026).



