Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Используя понятие С-точной пары [4], мы доказали [2], [4], что условие Коши сходимости числовая последователь­ность (a) можно записать в эквивалентной и соответствующей определению Э. Вайс-штейна   [12, p. 355] следующей форме

                    (0.1)

Там же предельное значение неограниченной конечным числом последовательно­сти Коши (a) мы назвали бесконечно большим числом Ω(a) и { Ω(a) } Ω.

1. О достаточности необходимого признака сходимости числового ряда

Обозначим символом Z_n сумму n первых членов a_i числовой последовательности

(а) (a ₁, a₂, •••, a_n,....), n ∈N:  a ₁ +a₂ +.....a_n, а символом S_n - число, равное значению суммы . Так что

^∑_n+1 = Σ_n + a_n+1   и  S_n+1  = S_n + a_n+1 , n ∈N.                                  (1.1)

Определение 1.1. Числовым рядом, определяемым последовательностью (a), назо­вём пару последовательностей (Σ_n) и (S_n), заданных посредством (1.1), и будем пи­сать

 a ₁ ⁺a₂ +............... + a_n+ А.                                      (1.2)

Ниже суммирование у символа Σ предполагается, по умолчанию, от 1 до ∞, что означает неограниченную возможность перехода от суммы  Σ_n  к сумме  Σ_n+1. Равенство a_n = f(n), n ∈N, называют также формулой общего члена ряда А.

Определение 1.2. Числовой ряд А называется сходящимся к числу А, если к этому числу сходится числовая последовательность (S_n) значений  S_n  частичных сумм  Σ_n этого ряда. Предельное значение А последовательности (S_n) называют суммой ряда А и пишут

limS_n = A.                      (1.3)

Если предел (1.3) не существует или равен ±<х>, то соответствующий ряд А называ-ется в анализе расходящимся. Из множества расходящихся в классическом смысле чи­словых рядов мы выделяем класс рядов, для каждого из которых числовая последова-тельность (S_n) значений S_n частичных сумм Σ_n  сходится к соответствующему беско­нечно большому числу (ББЧ) Ω(a) .

Необходимым для (1.3) является выполнение очевидного равенства

                    (1.4)

Равенство (1.2) можно записать в следующем виде

(А)= Σ a_n =(a₁+a₂ +..........+a_n) + ()  Σ_n + ρ_n.                    (1.5)

Бесконечную сумму ρ_n в  (1.5), называемую n-м остатком ряда А, обычно не отличают при записи от её значения r_n. Тривиальность предела последовательности ( r_n ) значений r_n остатков ρ_n ряда А является как и (1.4) необходимым для существова-ния суммы ряда А, то есть для предельного равенства (1.3):

limr_n = 0.                              (1.3')

Необходимые признаки (1.4) и (1.3') объединяет ниже Теорема 1.1 [1 p. 12].

Теорема 1.1. Для произвольного числового ряда Σa_n   справедлива при n →∞ следующая эквивалентность:

(r_n →0)<=>(a_n →0).

• Так как a_n = r_n-1-r_n , то, очевидно, что (r_n →0)=>(a_n →0). Пусть, далее,  и , p > k , суть значения соответствующих частичных сумм и Σ_k ряда (A) и Σ_k ⊂ Σ_p.   Если ,то для каждого k остаток ряда и    . Здесь, не нарушая общности рассуждений, пару (k, p) переменных k и p можно считать С-точной парой [4] и принять, например, p=k+q(K), где 0 < q(k) < C . Поэтому в силу (1.4)

 =  (a_k+1 + a_k+2 +... + a_k+q(k) ) =0. ■

У другой формулировки Теоремы 1.1 доказательство короче.

Теорема 1.2. Необходимое условие сходимости числового ряда является достаточным условием его сходимости.

• Предельное равенство lim( S_n- S_n_₁ )= lim a_n =0 есть условие (0.1) фундаментальности последовательности (S_n) значении S_n частичных сумм Σ _n числового ряда A. Поэтому для такого ряда справедливо предельное равенства (1.3), где А есть либо конечное число, либо равно некоторому ББЧ. И, значит, r_n ->0. ■

2. О сходимости знакопеременных рядов

Числовой ряд A = Σ a_n   называется знакопеременным, если количества его как положительных, так и отрицательных слагаемых не ограниченны. Такой ряд назы­вается абсолютно сходящимся, если сходится ряд, составленный из модулей его слагаемых. В противном случае говорят об «условной» или «неабсолютной» сходимости знакопеременного ряда. Очевидно, что абсолютно сходящиеся ряды сходятся «быстрее», чем условно сходящиеся, что мы и покажем на Примере 3.3.

В своей диссертации Бернгард Риман излагает [5, I. XII. 3] одно из свойств знакопеременных рядов следующим образом:

«... бесконечные ряды разделяются на два существенно различных класса, смотря потому, остаются ли они сходя-щимися, если сделать все слагаемые по­ложительными, или же этого нет. В пер-вом случае члены ряда могут быть как угодно переставляемы, во втором же сумма ряда, напротив, зависит от поряд-ка членов. В самом деле, пусть в ряде вто­рого класса положительные члены будут

a ₁, a₂, a₃, ..., а отрицательные -b ₁, -b₂, -b₃, ... . Тогда ясно, что суммы Σa и Σ b должны быть расходящимися; действи-тельно, если бы обе были сходящимися, то и весь данный ряд сходился бы после вы­равнивания знаков; если бы сходилась только одна, то данный ряд был бы рас-ходящимся. Нетрудно видеть, что при надлежащей перестановки членов ряд может принять любое заданное значение С. В самом деле, станем брать по очереди сначала положительные члены ряда, пока их сумма не превысит С, затем отрица-тельные, пока сумма не станет меньше С; при этом отклонение суммы от С ни­когда не станет больше, чем абсолютное значение члена, предшествующего послед­ней перемене знака. Но так как величины a и b c возрастанием индекса становятся бесконечно малыми, то отклонения от С при достаточном продолжении ряда ста-нут сколь угодно малыми, а это значит, что ряд сходится к величине С ... ».

Ниже излагается иная точка зрения по этому вопросу, основанная в частности на разделении понятий частичной суммы числового ряда и его остатка на собственно суммы и значения этих сумм.

Следуя почти точно Б. Риману, мы вводим для знакопеременного числового ряда А такие обозначения:

 (2.1)

Тогда ∀n ∈ N, S_n = P_m + Q_l, и, как доказано ниже (Теорема 2.3), если limP_m   P_∞, lim Q_l Q_∞, то всегда верно равенство A = Q_∞ + P_∞ . Вначале докажем для знакоперемен­ного числового ряда А следующее ниже утверждение [1, p. 18].

Теорема 2.1. Ряд В, являющийся произвольной перестановкой знакопеременного не абсолютно сходящегося к некоторому числу А ряда А, сходится к тому же числу А.

• Пусть сходящийся к числу В ряд В:

=                             (2.2)

получается отображением φ: N → N , φ(k)=j, a_k b_j , из ряда A:

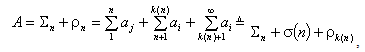(2.3)

А->В(1)->В(2)->...->В(n)->....                                      (2.4)

Следуя [6, 3.52], ряд В(n) называется перестановкой ряда В(n-1). Как результат процесса (2.4), мы получим из тождества

                   (2.5)

для каждого n ∈ N  следующие равенства:

                        (2.6)

где сумма , n_i < k (n), содержит те слагаемые из частичной суммы  Σ_k(n) ряда А, которые не вошли в частичную сумму ряда B (n) и . Эти преобразования иллюстрирует Рисунок 2.1:

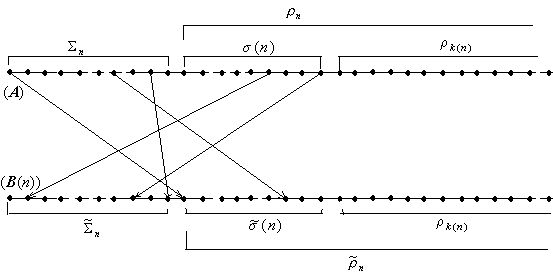
Рис. 2.1.

Отметим, что при переходе B (n)->B (n+1) переставляется не более одного из не более чем k(n +1) - n первых слагаемых остатка ряда B (n), а все члены этой суммы, предшествующие переставляемому слагаемому, сдвигаются в на одну позицию «в право». Отметим также ещё, что количества слагаемых в суммах Q(n) и (n) равны. Из (2.6) получаются для всех neN следующие равенства

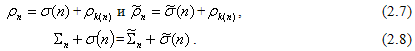
Обозначая значения сумм  и Q(n) символами и s(n), соответственно, получим эквивалентное (2.8) числовое равенство

            (2.9)

Равенство (2.8) и, следовательно, (2.9) для каждого n ∈ N  можно доказать методом математической индукции, исходя из тождества (2.5).

Так как сумма  входит в остаток ρ_n ряда А, а сумма входит в остаток ряда В(n), то в силу (2.3)-(2.7) и (2.9) , и

Теперь мы получаем из (2.9) при предельном переходе следующий результат:

Таким образом, при  n → ∞ в силу предположений   →  B,  S_n → А  следует  импликация: (→0, r_n→0)=>(B=A).  ■

В общем случае, из равенства (2.8) следует при  S_n->A и  r_n->0 эквиваленция: (   →  B)<=>( →(A-B)), то есть доказано следующее утверждение:

Теорема 2.2. Если для произвольного числа В из членов сходящегося к числу А знакопеременного ряда А построена произвольным образом последовательность (Σ_n^*) сумм Σ_n^* , последовательность значении S_n^* которых сходятся к числу В, то последовательностъ (r_n^*  ), получающихся при этом остатков r_n^* , сходится к числу А-В.

Замечание 2.1. В доказательстве Теоремы 2.1 условие не абсолютной сходимости исходного ряда (А) не использовалось, то есть Теоремы 2.1 и 2.2 справедливы для любого сходящегося ряда. Но в случае не абсолютной сходимости ряда (A) Q_∞ и P_∞ будут равны соответствующим бесконечно большим числам: Q_∞,P_∞ ∈ Ω, так как, например, при m →∞  Q_m -Q_m_₁ = q_m → 0 . Это предельное равенство является условием (0.1) фунда-ментальности числовой последовательности (Q_m). Поэтому Теорему 2.1 следует считать обобщением на знакопеременные ряды соответствующей Теоремы Дирихле о знакоположительных рядах.

Более того, Теорема 2.2 имеет следующее очевидное обобщение.

Теорема 2.3. Если числовая последовательность (a), определяющая сходящийся к числу А числовой ряд А, разбита произвольным образом на две подпоследовательности (a^* )и (),

и каждая  из этих подпоследовательностей определяет , соответственно, числовые ряды A^* и  , у которых последовательности (S_n^*) и () значении S_n^*  и    частичных сумм  Σ_n^*  и , соответственно , сходятся к некоторым числам (или к некоторым бесконечно большим числам) A^*  и , соответственно, тогда A^*  + =A.

Замечание 2.2. Теорема 2.3 обобщает очевидное свойство неизменности сходимо­сти числового ряда, когда при m → ∞ одна из сумм Σ_n^*  и , n + k = m, содержит конечное количество слагаемых.

В [7, IV. 1] дано «описание некоторых возможных типов сходимости ряда  элементов x_i произвольного линейного векторного пространства» в зависимости от вы­бора типа суммирования слагаемых ряда, в том числе отмечены: упорядоченная сходи-мость (A), перестановочная сходимость (B), неупорядоченная сходимость (C) и сходи-мость по подпоследовательностям (D). Перестановочная сходимость в [8, с. 4] называется безусловной сходимостью. Как следует из Теорем 2.1-2.3, справедливость которых сохраняется и для рядов  элементов произвольного линейного векторного пространства, отмеченные выше типы сходимости эквивалентны.

Более того, если как-то иначе чем в этой статье определённая сходимость числово­го ряда, не является регулярной (вполне регулярной), то соответствующее определение или его интерпретация или и то, и другое является некорректным.

3. Примеры

Пример 3.1. Пусть А= =А=ln2. Из условно сходящегося ряда А в [9, с.316-319] ряд В(p, q) «получен следующей процедурой»: после каждыхp последователь­ных положительных слагаемых ряда А ставилось q последовательных отрицательных членов этого ряда. Будем шаг за шагом выполнять, следуя [2, с. 107], указанную выше процедуру и обозначать получающийся на n-м шаге ряд символом В_n (p, q) . Получаемая при этом последовательность () значений частичных сумм  рядов сходится к числу В(p, q)=ln(2 ) и при p ≠ q  А ≠ В(p, q).

Покажем, однако, что, если, например, p>q, p + q = 2k , то при n=2ks и s=1, 2, 3,... → (А-В(p, q))>0, где - значение остатка  . Очевидно, что (см. (2.6))

          (3.1)

где

Используя следующие ниже два равенства из [9, с. 316-319]:

                                  (3.2)

где С_e - постоянная Эйлера, а γ_n →0, мы получим последовательно следующие ниже оценки значений S_n  и частичных сумм Σ_n и , соответственно, и значений r_2k и остатков р_n и рядов А и  :

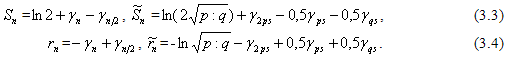
Оценка остатка в (3.3) получена из (3.1) с помощью равенств (3.2) по формуле

Учитывая (3.3) и (3.4), методом математической индукции можно доказать, что для всех n, n ≥ p+q, 

=ln (2 ) - β_n,    = - ln()+ β_n,   где    β_n →0,   и   lim = - ln( ) = A - B (p, q)), (cp. [11, S. 138-139], [10, VIII. 195]).

Это результат имеет простое объяснение: в остатках рядов при  p > q "накап-ливаются" отрицательные слагаемые.

С другой стороны, если рассмотреть без связи с рядом А, например, такой ряд B^* 1 +1/3 -1/2 +1/5 +1/7 -1/4 +1/9 +....., то каждая частичная сумма S*_n этого ряда будет равна соответствующей частичной сумме   ряда  , если у последнего взять p=2 и q=1. Поэтому lim S_n^* = ln 2 √2 , но, что легко показать, остаток r_n^*  ряда B^*  стремится к нулю. Это означает, что в отличие от каждого ряда ряд  B^* не является перестанов­кой ряда А. Аналитически отображение φ: N → N , которое определило бы переход A →> B^*  , можно задать следующей формулой:

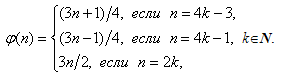
Очевидно, что данная функция φ не удовлетворяет необходимому предельному ус­ловию сюръективности отображения N → N, другими словами, оно является неосуществимым на всём множестве N. Это условие получено автором в работах [1-4].

Пример 3.2. Сложив у ряда А= каждые два очередных слагаемых ряда мы получим следующий      сходящийся  знакоположительный  числовой  ряд 

А^** =  = A = ln 2 , здесь n = 2k - 1 ∈ N

Пример 3.3. Выполним над членами ряда  А=  из Примера 3.1 следующие операции: в каждой последовательной четвёрке слагаемых сложим первый с четвёртым и второй с третьим членом. Так полученный ряд

будет абсолютно сходящимся к тому же числу А=ln2 числовым рядом, и сходящимся «в два раза быстрее» исходного ряда А.

СПИСОК ЛИТЕРАТУРЫ:

• 1.  Sukhotin A.M. Alternative Analysis Principles.-Tomsk: TPU EPF, 2002.
• 2. Начало высшей математики. Томск: Изд-во ТПУ, 2004.
• 3. Sukhotin A.M. From G. Galilei's paradox to alternative analysis // 4ecm, List of posters, Section 13.13 (Real analysis), Stock­holm, 2004.
• 4. Сухотин, А. М. Приложение по-нятия С-точной пары в анализе //Современные проблемы науки и образо-вания, 2007, 5.
• 5. Риман, Б. Сочинения. - М.; Л.: Гостехиздат, 1948.
• 6. Рудин, У. Основы математического анализа. - М.: Мир, 1966.
• 7. Дэй М.М. Нормированные линей-ные пространства. - М.: ИЛ, 1961.
• 8. Кашин, Б. С, Саакян, А. А. Орто-гональные ряды. - М.: АФЦ, 1999.
• 9. Фихтенгольц Г. М. Курс диффе-ренциального и интегрального исчисле­ния..- М.: Наука, 1967.-Т. 2.
• 10 Харди, Г. Г. Курс чистой матема-тики.- М.: Изд-во ИЛ, 1949.
• 11. Knopp K. Theorie und Anwendung der unendlichen Reihen. - Berlin: Springer-Verlag, 1922.
• 12. Weisstein Eric W. CRC Concise Encyclopedia of Mathematics. 2^nd ed. - Lon­don-New York: Chapman&Hall/CRC, 2002.