Введение
В данной статье, в рамках плоской модели, изучается вращение ротора со слоем жидкости на стенке камеры при вязкоупругом действии вала. Предполагается, что границей свободной поверхности жидкости является окружность с центром на оси вращения, а сама она вращается вместе с ротором, как твердое тело.
Материал и методы исследования
Исследование жидкостных автоматических балансирных устройств (АБУ) сводится к задаче о движении вращающихся тел с полостями, частично заполненными жидкостью [2]. Эта задача сопряжена с математическими трудностями, т.к. требует рассмотрения совместного движения твердого тела и жидкости. Известно ограниченное количество работ, в которых решается указанная задача применительно к АБУ. Так в [3, 4, 6] рассмотрена устойчивость стационарного вращения ротора, частично заполненного жидкостью со свободной поверхностью. Изгибные колебания вала с неуравновешенным диском на нем изучены в [5]. В [1, 7] показано влияние жидкости во вращающемся роторе на автоматическую балансировку механической системы без учета сил сопротивления. Ниже рассматривается установившееся движение неуравновешенного ротора с жидкостью при наличии внешнего сопротивления.
Результаты исследования и их обсуждение
Пусть ротор 1 (рис. 1), содержит камеру 2 частично заполненную однородной несжимаемой жидкостью 3, симметрично закреплен на гибком вертикальном валу, проходящем через геометрический центр О1. Центр масс ротора (точка Р) смещен от О1 на расстояние О1Р=е. При вращении ротора вал смещается на величину О2О1=a, а несжимаемая однородная жидкость, плотностью ρ, перетекает в сторону прогиба вала. При установившемся движении жидкость во вращающемся роторе занимает цилиндрический слой высотой h, свободной поверхностью которого является окружность радиуса r2 с центром на оси вращения AB (точка О2) и вращается с угловой скоростью 
[6]. Отсюда центр масс слоя жидкости находится на линии центров О2О1 в точке G, а движение ротора является плоским.
Введем в плоскости движения точек O1, G, P две системы координат с общим началом в точке О2 на линии AB: неподвижную систему О2ξη и подвижную О2ху, ось x которой параллельна отрезку О1Р. Угловые скорости вращения ротора и системы О2xy одинаковые, следовательно, ротор в подвижной системе координат неподвижен. За обобщенные координаты возьмем координаты точки О1 в подвижной системе О2xy – x,y.
а)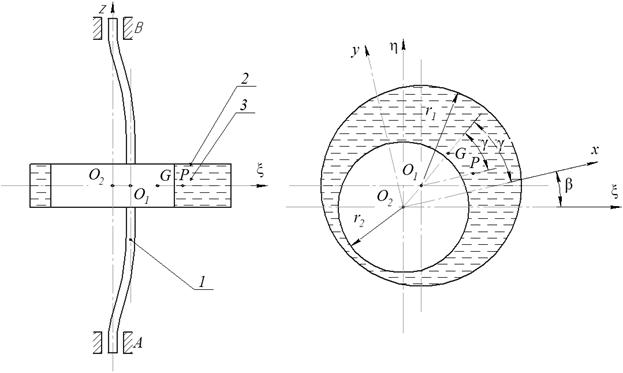
б)
Рис. 1. а – Схема закрепления ротора; б – Сечение ротора с жидкостью
На ротор со стороны вала действует сила упругости 
и сила внешнего трения, приложенная в точке О1, пропорциональная абсолютной скорости 
этой точки, 
Где c и χ коэффициенты упругости и внешнего трения. Природа этих сил подробно изложена в [9]. Так, силы внешнего трения вызываются вязким сопротивлением внешней среды, опор, специальных демпферов и зависят от скоростей абсолютных перемещений точек ротора и вала; силы внутреннего трения порождаются сопротивлением частиц материала и в первом приближении принимаются пропорциональными скорости деформации вала. Согласно принципу Даламбера имеем уравнение равновесия главных векторов внешних сил и сил инерции:
. (1)
Здесь m1 и m2 – массы ротора и жидкости, 
и 
– переносные ускорения точек Р и G соответственно. Координаты этих точек определяются выражениями:
(2)
где 
– коэффициент, характеризующий наполнение камеры; 
– радиус камеры, 
– радиус внутренней поверхности жидкости.
Проецируя (1) на оси х, у и используя (2) для вычисления 
, 
и 
, получаем уравнения стационарного движения системы:
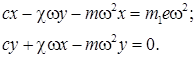(3)
Здесь 
, 
– масса ротора, 
– масса жидкости.
Из уравнения равновесия моментов всех сил относительно оси AВ, можно определить вращающий момент, приложенный к валу со стороны двигателя. Считаем, что двигатель развивает усилие, обеспечивающее заданное вращение ротора.
Решение уравнений (3) имеет вид:
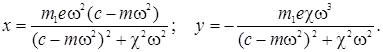(4)
Полагая в (4) χ=0, получаем решение для однокамерного АБУ без внешнего сопротивления, рассмотренное в [9]. По формулам (4), (2) вычисляется прогиб вала 
и отклонение центра масс системы от оси AB 
, которые в безразмерных переменных принимают вид:
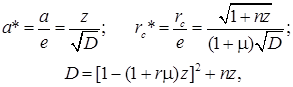(5)
где 
– квадрат отношения частоты вращения к собственной частоте ротора, 
– безразмерный коэффициент сопротивления, 
– отношение массы жидкости к массе ротора.
Угол сдвига фазы движения γ (рис.2) определяется формулой:
. (6)
Это выражение соответствует отсутствию жидкости, т.е. при m=m1.
Из выражений (4–6) следует, что при ω→∞ (z→∞) a→m1e/m, т.е. прогиб вала становится меньше неуравновешенности е, т.к. m1/(m1+rm2)<1; rc→ 0, γ→ π, x→ -m1e/m, y→0; координаты центров масс ротора и слоя жидкости принимают значения: xp=rm2e/m, yp=0; xG=-rm1e/m, yG=0.
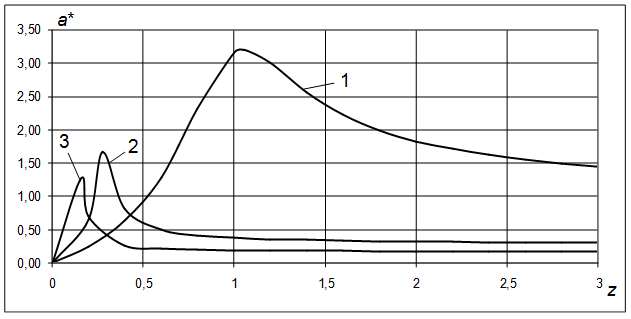
Рис. 2. Зависимость прогиба вала от угловой скорости ротора при r=5,26, n=0,1 кривые соответствуют: 1 ─ μ =0; 2 ─ μ =0,5; 3 ─ μ =1
Таким образом, при больших угловых скоростях вращения ротора ω центр масс системы стремится занять положение на оси вращения AВ; происходит самоцентрирование системы.
Расчеты, проведенные по формулам (5), частично иллюстрируются на рис. 2. Видно, что с увеличением массы жидкости в роторе происходит уменьшение критической скорости, при которой прогиб вала достигает максимума (появляется резонанс) [8]. Дальнейший анализ расчетов показывает, что с увеличением внешнего сопротивления при неизменном μ критическая скорость и соответствующий ей прогиб уменьшаются, а самоцентрирование системы (rc→0) ускоряется.
При постоянном сопротивлении (n=const) увеличение массы жидкости (параметра μ) так же ускоряет самоцентрирование системы. Критическая частота вращения ротора при одних и тех же значениях n и μ уменьшается с ростом параметра r.
Выводы
Результаты проведенной работы показывают, что увеличение массы жидкости в роторе уменьшает его критическую скорость вращения. Внешнее трение ускоряет самоцентрирование системы. Полученные соотношения позволяют производить выбор конструктивных параметров жидкостного АБУ, работающего в заданном диапазоне угловых скоростей ротора.
Рецензенты:
Тарасов Сергей Юльевич, д.ф.-м.н., с.н.с. ИФПМ СО РАН, г. Томск.
Пушкарев Александр Иванович, д.ф.-м.н., сотрудник ООО «Инженерно-физический центр», г.Томск.