Введение
Существует ряд прикладных задач, где требуется управлять объектом в положении неустойчивого равновесия [1]. Оценку эффективности предлагаемых решений часто проводят по результатам решения классической задачи механики и теории управления, заключающейся в приведении двухзвенного маятника из произвольного начального положения в произвольное неуравновешенное состояние и удержания ее там. Это связано с тем, что уравнение состояния такой динамической системы представляет собой упрощенную модель механического двухзвенного манипулятора робота с безредукторными приводами и абсолютно жесткими элементами конструкции. Управление таким объектом осуществляется за счет изменения вращающих моментов в шарнирах устройства.
Их решение достигается как классическими методами, базирующимися на принципе максимума Л. С. Понтрягина [9] или методе динамического программирования Р. Беллмана [4], так и основанными, к примеру, на концепции обратных задач динамики, функциях Ляпунова, идее декомпозиции [1, 7]. Однако недостатком первых является то, что решение задачи синтеза для нелинейных систем получено только для частных случаев. Для второй группы методов, как правило, характерно введение различного рода упрощений и ограничений [1, 7].
Работы [2, 3, 5, 6] показывают, что использование механико-математического приема, названного объединенный принцип максимума, позволяет получить оптимальные, конструктивные, достаточно просто реализуемые на практике решения. Полученные в работе управления определены с точностью до синтезирующей функции. Для ее построения в статье предлагается использовать метод анализа поверхности переключения в фазовом пространстве переменных Лагранжа, где обобщенная сила меняет знак и выполняется условие постоянства обобщенного кинетического потенциала.
Проведенное математическое моделирование показало высокую эффективность использования объединенного принципа максимума, заключающуюся в повышении точности расчетов, уменьшении сложности процедуры синтеза и вычислительных затрат в сравнении с классическими [5, 7, 9].
Постановка задачи. Движение управляемой системы подчиняется принципу Гамильтона – Остроградского, согласно которому обращается в нуль величина [8]:
, 
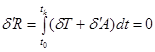. (1)
Целевой функционал представлен следующим выражением:
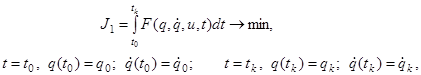
(2)
где 
– обобщенные координаты и скорости, 
– определенно-положительная функция, 
– кинетическая энергия, 
– элементарная работа обобщенных сил, зависящих от управлений, 
.
Из принципа (1) следуют уравнения Лагранжа второго рода:
. (3)
Требуется определить такие управления 
или 
, которые переводят систему (3) из начального состояния 
в конечное 
, при условии минимума целевого функционала (2).
Объединенный принцип максимума. Теорема [5, 6]. Условие экстремума (2) определяет максимум функции обобщенной мощности:
. (4)
где 
– фиктивная сила, зависящая от формы целевого функционала, при этом 
, а на концах траектории 
выполняются условия трансверсальности для функции Гамильтона – Остроградского и обобщенного кинетического потенциала:
, (5)
. (6)
Основные элементы доказательства. Использование техники асинхронного и игольчатого варьирования к расширенному функционалу (2) приводится к условиям трансверсальности (5), (6) и асинхронной вариации функционала для произвольной обобщенной силы 
:
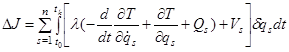. (7)
Из сравнения (7) и асинхронной вариации 
, полученной для 
, при 
, 
, 
, 
, 
, 
, следует выражение второй вариации функционала:
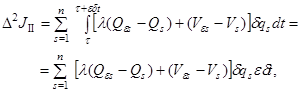. (8)
При предельном переходе: , , , , , получаем:
. (9)
Если обобщенная сила 
выбрана так, что неравенство выполняется для любых 
, то из (9) вытекает теорема объединенного принципа максимума (4). Из (4) следует, что обобщенные силы с точностью до синтезирующей функции 
находятся из выражения:
, (10)
которое определяет в фазовом пространстве гиперповерхности переключения управления.
Построение синтезирующей функции на основе метода представления траектории в фазовом пространстве. Так как гиперповерхности переключения обобщенная сила равна нулю, условия трансверсальности (6) преобразуются в условие постоянства обобщенного кинетического потенциала в данный момент времени:
. (11)
Это уравнение представляет собой поверхность гиперболического параболоида в фазовом пространстве переменных Лагранжа 
.
Преобразование Лежандра функции 
по переменным 
есть функция Гамильтона (5), представляющая поверхность эллипсоида в переменных Гамильтона 
:
, (12)
в которой величины 
выражены через 
, при помощи уравнений:
(13)
для обобщенных импульсов, при этом преобразовании величины 
играют роль параметров. 
– алгебраическое дополнение элемента 
гессиана кинетического потенциала:
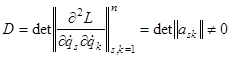. (14)
На поверхности эллипсоида переключения управления канонические уравнения Гамильтона имеют вид:
, (15)
так как кинетический потенциал системы на поверхности:
. (16)
Синтезирующая функция записывается в следующем виде [6]:
, (17)
имеющая смысл углового коэффициента касательной к траектории на поверхности переключения.
Пример. Рассмотрим двойной механический маятник [2, 3] (рисунок 1).
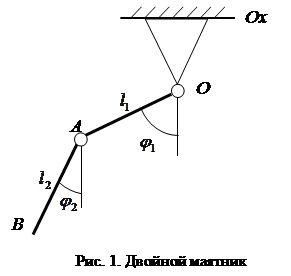
Выбор в качестве обобщенных координат углов 
и 
позволяет записать кинетическую и потенциальную энергию такой системы в следующей форме:
, (18)
, (19)
тогда уравнения Лагранжа второго рода (3) принимают вид:
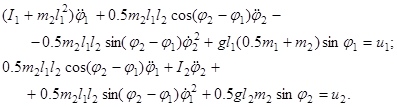(20)
где 
– ускорение свободного падения; 
, 
– массы стержней; 
, 
– длины стержней.
Требуется синтезировать законы ограниченных управлений 
таких, что двойной маятник можно перевести из произвольного начального положения: 
в произвольное неуравновешенное состояние 
, 
и управлять заданным движением 
относительно этого нового положения уравновешенности [8].
Функционал качества управления имеет вид:
. (21)
Оптимальные решения для кусочно-постоянных управлений полученные методом объединенного принципа максимума имеют вид [5, 6]:
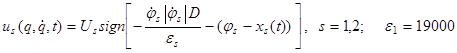, (22)
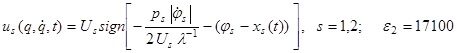, (23)
где 
. Достигнутые значения целевого функционала составили 
и 
соответственно.
Оптимальное решение в классе кусочно-непрерывных управлений, полученное методом объединенного принципа максимума, записывается в следующей форме:
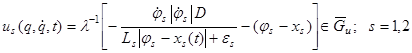. (24)
Здесь 
; 
; 
; 
; 
; 
Достигнутое значение целевого функционала 
. Результаты математического моделирования приведены на рисунках 2–3.
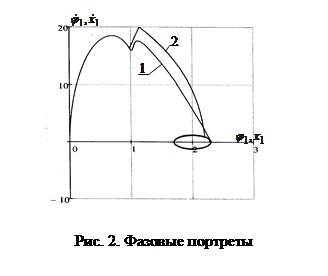
На рис. 2 показаны фазовые портреты: линия 1 – решение в классе кусочно-непрерывных управлений; линия 2 – решение в классе кусочно-постоянных управлений.
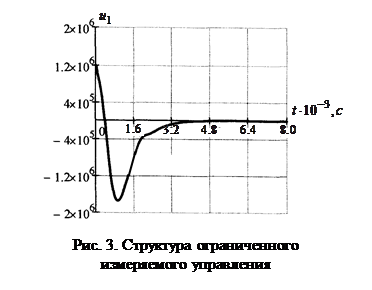
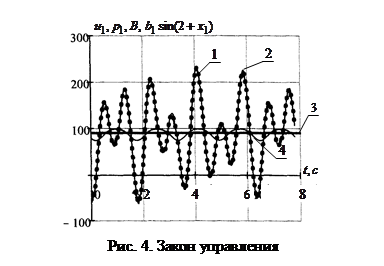
На рис. 3 показана структура ограниченного измеряемого управления. Достигнутое значение целевого функционала 
. При неограниченном росте параметра ограничения значение целевого функционала сколь угодно мало 
.
Выводы
Новый метод синтеза оптимального управления двойным маятником в неуравновешенном конечном состоянии с использованием синтезирующей функции по предлагаемому методу обладает универсальностью и простотой. Его применение для класса кусочно-непрерывных и кусочно-постоянных управлений и обеспечивает высокую точность расчетов, требует меньших вычислительных затрат в сравнении с известными решениями.
Исследование проведено при поддержке Министерства образования и науки Российской Федерации, соглашение 14В37.21.2067
Рецензенты:
Звездина Марина Юрьевна, доктор физико-математических наук, доцент, заведующая кафедрой «Радиоэлектроника», Минобрнауки России, Ростовский технологический институт сервиса и туризма (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса», г. Ростов-на-Дону.
Риполь-Сарагосси Татьяна Леонидовна, доктор технических наук, профессор, заместитель директора по дополнительному образованию, Минобрнауки России, Филиал государственного образовательного учреждения высшего профессионального образования «Московский государственный университет технологий и управления» в г. Ростове-на-Дону, г. Ростов-на-Дону.