Математическое описание радиотелескопа включает в себя неопределенность, которая определяется такими параметрами, как коэффициент жёсткости и коэффициент вязкости трения. Эти параметры изменяются в зависимости от разных факторов, таких как окружающая температура, скорость двигателя и др. На радиотелескоп существенное влияние оказывает внешнее возмущение - воздействие ветра. Рассматривается робастный подход к синтезу H∞-управления для решения данного комплекса вопросов, также рассматривается адаптивное управление с эталонной моделью (ЭМ) для устранения влияния зазора на объекте радиотелескопа.
H∞-управление имеет несколько особенностей в сравнении с другими методами синтеза робастных контроллеров [2]
· Метод работает с критериями устойчивости и чувствительности системы.
· Простой одношаговый алгоритм.
· Точное формирование выходной частотной характеристики.
Математическое описание радиотелескопа включает в себя неопределенность, которая определяется такими параметрами, как коэффициент жёсткости и коэффициент вязкости трения. Однако, при этом не учитывается возмущение ветра. Параметры меняются в зависимости от разных факторов, таких как изменение температуры, скорости и др. Их изменение приводит к изменению характеристик системы, что в свою очередь приводит к тому, что регулятор становится не действующим. Достигнуть желаемого результата невозможно, потому что регулятор настроен для системы с другими внешними условиями.
Робастное управление обеспечивает качество и устойчивость системы.
G(s)- обозначает объект управления.
K∞(s)- обозначает регулятор, получаемый от робастного алгоритма.
При расчёте регулятора алгоритм обеспечивает три критерия [3]:
I. Критерий устойчивости: корни характеристического полинома 1+G(s)K∞(s)=0 должны находиться на левой половине S-плоскости.
II. Критерий качества: известен как функция чувствительности S(s)=1/ 1+G(s)K∞(s), которая должна имеет маленькое значение при частотах возмущения.
III. Критерий робастности: это поддержка качества и устойчивости при разных рабочих условиях.
На рисунке 1 показана структура замкнутой системы с робастным регулятором. Система включает в себя описание объекта управления, выходных весовых функций, входных сигналов (задание и возмущение) и регулятора, имеющего робастный характер.
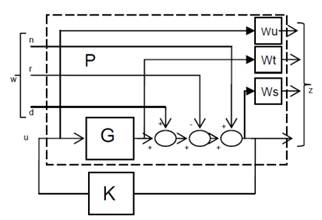
Рис.1
Объект управления P имеет два входа, два внешних воздействия w, которые включают задаточный сигнал и возмущение. Контролируемая переменная обозначена u. Это вектор выходных сигналов системы, состоящий из сигнала ошибки z, который надо минимизировать, и измеренной переменной v, которая используется в контуре управления. В K используется v для подсчёта переменной u.
Уравнение системы:
![]()
![]()
таким образом, можно выразить зависимость z от w:
![]()
и далее:
![]()
таким образом, целью H∞-оптимального управления является синтез такого регулятора K, Fl(P,K), который минимизировал бы H∞-норму системы. Норма на бесконечности матрицы Fl(P,K) определяется как:
![]()
где ͞σ - максимальное сингулярное число матрицы Fl(P,K)(jω) .
Найденный таким образом регулятор является оптимальным в H∞-смысле[4].
Для расчёта регулятора требуется определение весовых функций Ws, Wt и Wu, которые определяют характеристики чувствительности и качество замкнутой системы. В результате, получаемый регулятор обеспечит эти требования. Весовые функции имеют следующие описания:
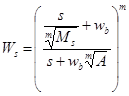 ;
; 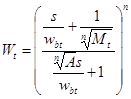
где Ms, Mt - максимальные значения амплитуды при высоких частотах, A - это качество (слежение за ошибкой) при малых частотах, wb, wbt- частоты среза.
Порядок регулятора зависит от порядка объекта и функций Ws и Wt, порядок регулятора = N+n+m, где N это порядок объекта, поэтому n и m должны быть как можно меньше.
Описание однодиапозонного электроприводного радиотелескопа 8-ого порядка, где вход - это двигатель с контуром тока, а выход - это скорость зеркала.
Расширенный объект P включает в себя описание радиотелескопа и весовых функций и определяется как MIMO объект
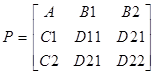
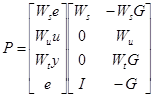
Полученный регулятор 10-ого порядка обеспечит больше 250% от неопределённости объекта при изменении параметров механической связи (коэффициентов жёсткости и вязкости трения).
Для того, чтобы устранить эффект зазора, который отображается в качестве автоколебания, при котором объект становится не стабильным, используется алгоритм адаптивного управления.
Адаптивная система, исходя из описания объекта и вводя аналогичное описание эталонной модели
![]() ,
, ![]()
где r- m- мерный входной командный сигнал,
![]()
где![]()
![]()
![]()
![]()
Дополнительное адаптирующее воздействие z построено по знаковому алгоритму. Сигнальная адаптация вида
![]()
![]()
![]()
где P- это решение уравнения Ляпунова.
Таким образом, адаптивный алгоритм (АА) наблюдает разницу момента упругости между объектом и моделью, сигнал ошибки e отражает влияние зазора, АА обновляет параметры робастного регулятора, пока ошибка существует (см. рисунок 2).
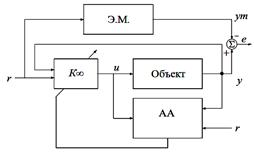
Рис.2
На рисунке 3 показаны результаты, получены в среде SIMULINK-MATLAB, скорость зеркала ω3 для объекта и ω3’ для эталонной модели и при сигнале задания скорости 5 рад/с, сигнал возмущения задаётся при 30с.
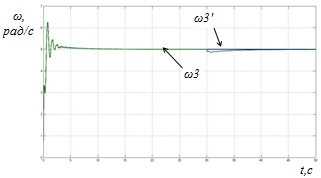
Рис.3
Объект имеет робастный характер для устранения влияния возмущения и изменения параметров радиотелескопа, адаптивный алгоритм успешно устраняет эффект зазора на объекте. С помощью одного двигателя можно запустить объект радиотелескоп и при этом получить весьма удовлетворительные результаты.
Рецензенты:
1. Поляхов Николай Дмитриевич, доктор технических наук, профессор, «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», Россия, 197376, Санкт-Петербург, ул. Проф. Попова, 5.
2. Зубков Василий Иванович, доктор физико-математических наук, профессор, «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», Россия, 197376, Санкт-Петербург, ул. Проф. Попова, 5.



