Постановка задачи
Пусть 
– полупространство 
евклидова пространства 
точек 
. Пусть 
конечная область в , симметричная относительно плоскости 
и ограниченная поверхностью 
. Обозначим через 
часть , расположенную в 
. Граница области разбивается 
и 
, расположенными соответственно на плоскости и в полупространстве . Поверхность является поверхностью класса 
, когда 
[3].
Рассмотрим краевую задачу: найти четное по 
решение уравнения
(1)
в области , 
раз непрерывно дифференцируемое в 
и удовлетворяющее граничным условиям
,
где
, если 
и 
, если 
, 
– внешняя нормаль к границе в точке 
, 
, 
– оператор Бесселя, 
– любое положительное число, 
. Уравнение вида (1) назовем В-полигармоническим уравнением [1].
Фундаментальное решение
Известно [2], что фундаментальные решения уравнения (1) с особенностью в начале координат имеют вид 
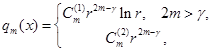
где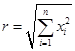 
, 
.
Значения 
и 
выберем таким образом, чтобы
(2)
и
(3)
для любой четной по 
бесконечно дифференцируемой и финитной в 
функции 
.
Можно проверить, 
удовлетворяет условиям (2) и (3) при следующих значениях и :
.
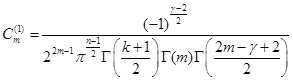
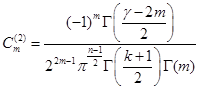С помощью непосредственного подсчета получаем, что
.
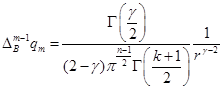Для получения фундаментального решения с особенностью в произвольной точке применим к функции 
оператор обобщенного сдвига 
[4]:
,
где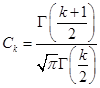 
.
Так как операторы и 
коммутируют, то в силу формальной самосопряженности оператора из формулы (3) следует, что
.
Формулы Грина для функций класса 
Пусть 
и 
четные по функции класса .
Тогда имеют место тождества
(4)
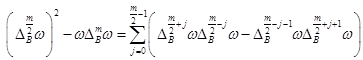(5)
при четном 
, и
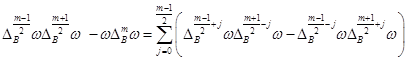(6)
когда – нечетное число.
Нам понадобятся, для четных по функций 
, первая формула Грина
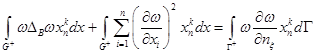
и вторая формула Грина
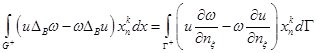. (7)
Интегрируя обе части тождеств (4)–(6) по области и пользуясь формулой (7), получим обобщенные формулы Грина
,
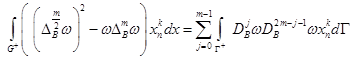для всех четных и
,
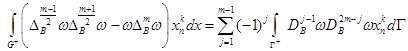когда – нечетное число, а также имеет место формула
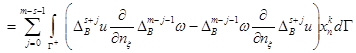
, (8)
где, если и , если , – внешняя нормаль к границе в точке .
Интегральное представление
Пусть 
– внутренняя точка области 
. Вырежем эту точку шаром 
с центром в точке и радиуса 
, такого что 
(если 
, то точку вырежем полушаром 
). Поверхность шара обозначим 
(
). Пусть 
– решение уравнение (1) в области 
.
Применяя формулу (8) к функциям 
и 
в области 
, с учетом равенства (2), получим
.
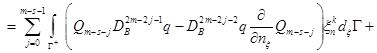
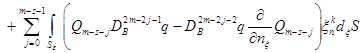Меняя переменную суммирования, и заметив, что 
и 
в 
, последнюю формулу можем записать в следующем виде
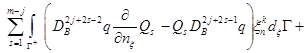
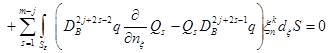. (9)
Используя схему, предложенную в работе [5], докажем, что для и 
, имеет такую же особенность в точке 
, что и фундаментальное решение оператора. Вводя обозначение 
, получим
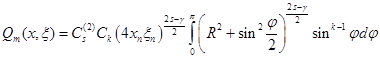. (10)
Разность между интегралом (10) и интегралом
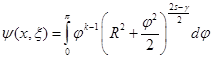
является регулярной функцией в точке , то есть для 
. В последнем интеграле сделаем замену переменной по формуле 
. В результате будем иметь
.
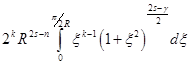Непосредственно вычисляется, что
.
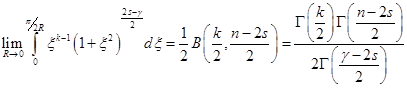Откуда
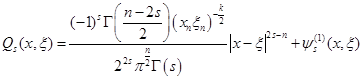. (11)
Используя приближенную формулу (11) получаем, что
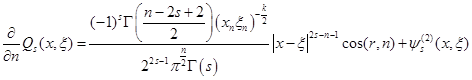(12)
где 
, и
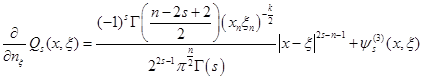(13)
Из приближенных формул (11)–(13) следует, что в формуле (9) первая сумма левой части не зависит от 
, во второй сумме все слагаемые, кроме слагаемого при 
и 
, сходятся к нулю. Вычислим предел слагаемого при . Его обозначим через 
. В силу теоремы о среднем значении интеграла, приближенных формул (11)–(13) и с учетом того, что 
при 
, получаем
,
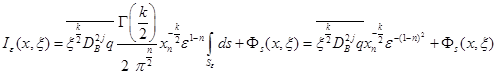то есть 
.
Таким образом, имеют место следующие интегральные представления для решения уравнения (1):
(14)
Отсюда при 
имеем, что
.
Заключение
В работе получено интегральное представление (14) найденного решения уравнения (1), необходимое для сведения краевой задачи к системе интегральных уравнений.
Рецензенты:
Игнатьев Ю.Г., доктор физико-математических наук, профессор, зав. кафедрой высшей математики и математического моделирования, Казанский (Приволжский) федеральный университет, г. Казань.
Сушков С.В., доктор физико-математических наук, профессор, зав. кафедрой теории относительности и гравитации, Казанский (Приволжский) федеральный университет, г. Казань.
Криштоп Виктор Владимирович, доктор физико-математических наук, профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Kwangwoon University, Korea.