Получение ленточных материалов путем прокатки в валковых прессах широко используются в химической промышленности в производстве строительных материалов. Описанию процесса прокатки посвящено большое количество научных работ.
Анализ конструктивных особенностей валкового оборудования для прокатки дисперсных материалов показал, что наиболее перспективным представляется использование в валковых машинах принудительного питания, причем рабочие органы питателей должны обеспечивать стабильное давление подпора. Однако процесс прокатки вязкоупругих материалов с давлением подпора остается малоизученным [2].
На рис. 1 представлена принципиальная схема расчета валковой машины с принудительным питанием.
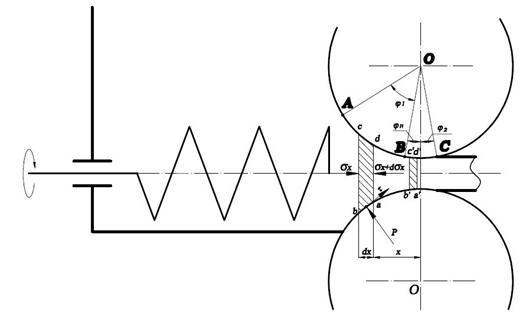
Рис.1. Принципиальная схема расчета валковой машины с принудительным питанием
При прокатке в валковом прессе можно указать две зоны различного поведения материала: зона АВ – зона отставания, где материал проскальзывает относительно валков, и зона ВС – зона опережения, где материал движется со скоростью, превышающей окружную скорость валков.
Условие равновесия выделенного элемента материала в зоне отставания АВ может быть записано в виде:
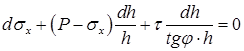, (1)
где σx – среднее нормальное напряжение сжатия, возникающее в прокатываемом материале; P – удельное давление на материал со стороны валков; τ – удельная контактная сила трения; φ – угол, определяющий положение элемента abcd, h – половина толщины полосы в сечении x очага деформации.
Введем безразмерную координату положения:
(2)
и параметр:
, (3)
где R – радиус валков; 2h0 – минимальная толщина очага деформации (вдоль прямой О1О2, соединяющей центры валков).
Учитывая, что h0<<R, можно получить следующие приближенные соотношения:
, (4)
. (5)
Формулы (2)-(5) позволяют переписать уравнение (1) в виде:
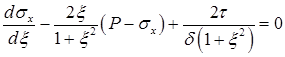. (6)
Для решения дифференциального уравнения (6) необходимо установить связь между σx и P, а также между τ и P.
При свободной прокатке дисперсных материалов, т.е. без давления подпора, σx играет роль бокового давления по аналогии с процессом прямого прессования, а P – роль давления подпора на материал. В случае прокатки с давлением подпора на материал элемент abcd испытывает двухстороннее сжатие: со стороны подающего шнека действует давление – σx и со стороны валков давление – P. Считая эти давления одинаковыми, получим
. (7)
Сила трения зависит не только от давления, но также и от скорости проскальзывания материала относительно поверхности валка, которая в свою очередь изменятся вдоль дуги контакта. Принимая, что максимальное значение силы трения достигается в сечениях входа и выхода материала из валков, а нулевое значение в нейтральном значении, можно в первом приближении записать:
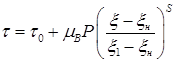, (8)
где ξ1 и ξн – безразмерные координаты сечения входа и нейтрального сечения; S – коэффициент, характеризующий степень проскальзывания; τ0 – связность материала.
Подставляя формулы (7), (8) в уравнение (6), получим дифференциальное уравнение, описывающее процесс в зоне отставания 
:
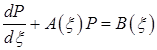, (9)
где
,
.
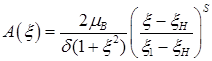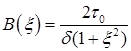Граничное условие равенства удельного давления подпора в сечении входа
, (10)
где PП – давление подпора, которое создается питающим шнеком при входе материала в пространство между валками.
В зоне опережения, которая соответствует участку дуги валка ВС, собственно процесса прокатки не происходит, т.к. плотность и толщина проката остаются практически неизменными после прохождения нейтрального сечения. За счет гидростатического напора, созданного в зоне отставания силами трения и удельного давления, материал выдавливается в зазор между валками.
Уравнение равновесия элемента a’b’c’d’ в зоне опережения записывается в виде
. (11)
С учетом выражений (4),(5) и из геометрии зоны деформации можно получить следующее приближенное соотношение для зоны опережения:
, (12)
что позволяет переписать выражение (2.56) в виде:
. (13)
При предположении, что предел текучести проката в зоне опережения остается постоянным, получим
. (14)
Зависимость силы трения от давления и скорости проскальзывания в зоне опережения определяется формулой:
. (15)
Подставляя формулы (14), (15) в уравнение (13), получаем дифференциальное уравнение, описывающее рассматриваемый процесс в зоне опережения 
:
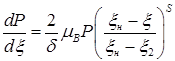(16)
с граничным условием:
. (17)
Координата сечения входа ξ1 определяется конструктивными особенностями узла питания; координата выхода ξ2 зависит от эластического восстановления прокатываемой ленты, которое составляет (15-20) %.
В соответствии с общей теорией упругости, напряжения сжатия, возникающие в прокатываемом материале, определяются формулой
, (18)
где относительные деформации εx, εy, определяются соответственно формулами
, (19)
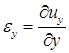, (20)
Относительная деформация в вертикальном направлении может быть определена из геометрии задачи
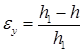, (21)
где h1– половина толщины полосы при входе в зону прокатки. В свою очередь половина толщины полосы h является функцией координаты x
. (22)
В соответствии с формулой (4) выражение (22) приводится к виду
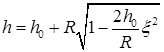. (23)
Тогда для относительной деформации εy и получим выражение
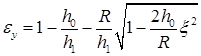. (24)
Подставляя формулы (18), (20), (24) в уравнение (9) и используя условие (19), для относительной деформации εx получим дифференциальное уравнение
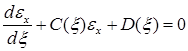, (25)
где величины
и
определяются выражениями
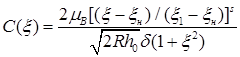, (26)
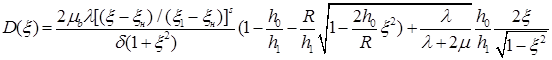. (27)
Начальное условие для уравнения (25) составим из следующих соображений. На входе в зону прокатки напряжение σx равно напряжению подпора PП. В результате получим
; 
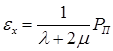. (28)
Уравнение (25) является дифференциальным уравнением первого порядка с начальным условием (28). Для его решения использовался метод Рунге-Кутты [1].
Зная относительные деформации εx, εy в зоне отставания можно определить порозность материала
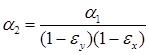, (29)
где α1– порозность материала на входе в зону прокатки.
Для проверки результатов модели были проведены экспериментальные исследования на лабораторной установке, принципиальная схема которой соответствует схеме, представленной на рис.1. В экспериментах использовался вязкоупругий материал, выполненный в соответствии с рецептурой [4]. Упругие характеристики материала и показатели трения определялись по методикам [3, 5]. Использовались валки диаметром 200мм, 300мм, 600мм. Число оборотов валков изменялось в пределах 5 – 20об/мин. Зазор между валками изменялся в пределах 10–30мм. Деформационные характеристики материала определялись по визуальным измерениям толщины готовой ленты. Для определения давления сжатия в поверхность одного из валков (верхнего) был вмонтирован тензопреобразователь. Сигнал тензопреобразователя поступал на цифровой регистратор с картой памяти. Регистратор с картой памяти и элементом питания имеют компактный корпус, который позволяет закрепить его на поверхности валка. После проведения эксперимента карта памяти извлекалась из регистратора и подключалась к компьютеру для обработки данных эксперимента.
На рис. 2 представлено сопоставление расчетных и экспериментальных данных по прокатке вязкоупругого материала в валковом прессе.
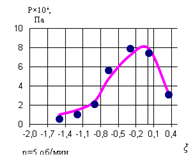
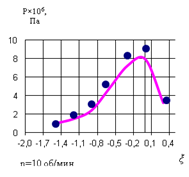
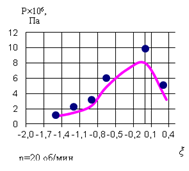
Рис. 2. Сопоставление теоретических и экспериментальных данных по давлению прокатки материала для валков диаметром 300 мм
Представленные данные свидетельствуют о хорошей сходимости теоретических и экспериментальных данных. На малых скоростях прокатки (при линейной скорости до 0,1м/с) расхождения не превышают 13 %.
Анализ модели показывает, что за счет давления подпора, которое обеспечивается питающим шнеком, достигается необходимое давления сжатия материала валками при меньших значениях диаметров валков, чем в обычных условиях работы.
Рецензенты:
Приоров Андрей Леонидович, доктор технических наук, доцент кафедры динамики электронных систем ФГБОУ ВПО «ЯрГУ», г. Ярославль.
Мурашов Анатолий Александрович, доктор технических наук, профессор кафедры общих математических и естественнонаучных дисциплин, Ярославский филиал Аккредитованного образовательного частного учреждения высшего профессионального образования «Московский финансово-юридический университет МФЮА», г. Ярославль.