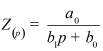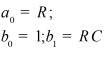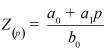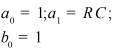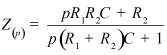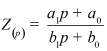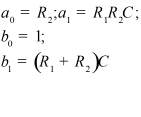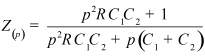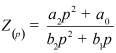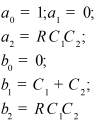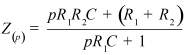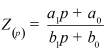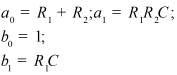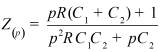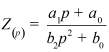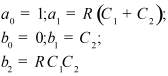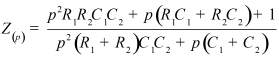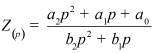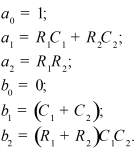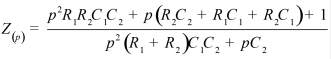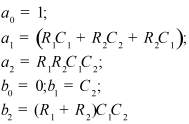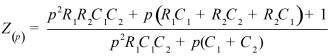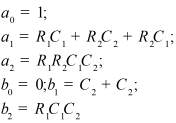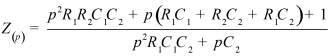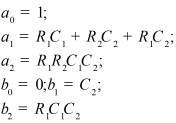Однако общепризнанной является методика, при которой кратность рентгенологического исследования составляет в среднем 1 раз в месяц [2]. Это обусловлено малой чувствительностью метода к незначительно меняющимся характеристикам регенерирующей костной ткани и лучевой нагрузкой, испытываемой организмом больного. Так при рентгенографии бедренной кости в 2-х стандартных проекциях лучевая нагрузка составляет 15-20 м.Зв. При условии ежемесячного повторения контрольной рентгенографии суммарная доза за период лечения от 2 до 6 месяцев составит 50-120 м.Зв [2].
Актуальность вопросов, возникающих при изучении параметров электрических цепей с двумя доступными узлами, называемыми двухполюсниками, постоянно растет. Это вытекает, с одной стороны, из большего числа такого рода задач в различных областях знания, а, с другой стороны, - из широкого развития средств измерительной техники, использующих операционные усилители (ОУ), микропроцессоры (МП), и персональные ЭВМ.
В литературе рассмотрены различные задачи, требующие определения параметров многоэлементных двухполюсников (ПМД), которые по области применения условно могут быть разделены на несколько больших групп:
- научные исследования;
- научные исследования;
- контроль радиоэлектронной аппаратуры (РЭА);
- преобразование неэлектрических величин в электрические величины;
- медицинская диагностика [1].
Вышеуказанные причины зачастую ведут к недооценке или переоценке рентгенологических данных, что влечет за собой увеличение сроков иммобилизации, ограничение двигательного режима больного или к осложнениям в виде рефрактур [5].
Использование для этой цели импедансного метода (суть которого состоит в изучении суммарного электрического сопротивления биообъекта) способно многократно повысить объективность получаемой информации при обследовании больных с переломами и удлинениями длинных трубчатых костей.
При использовании импедансного метода чаще всего измеряется электрическое сопротивление, которое потом пересчитывается в удельное сопротивление или проводимость. Импеданс биоткани имеет активную и реактивную (емкостную) составляющие [3]. Данный метод неинвазивный, что позволяет использовать его с большей кратностью. Параметры, определяемые в процессе измерений, объективно отражают состояние костной ткани в момент измерений и обеспечивают возможность в дальнейшем прогнозировать течение процессов репарации костной ткани.
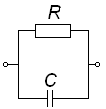
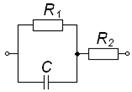
Все биологические объекты могут быть представлены в виде электрических схем замещения. Для двухэлементных двухполюсников возможны следующие два топологических варианта, представленные на рис 1.
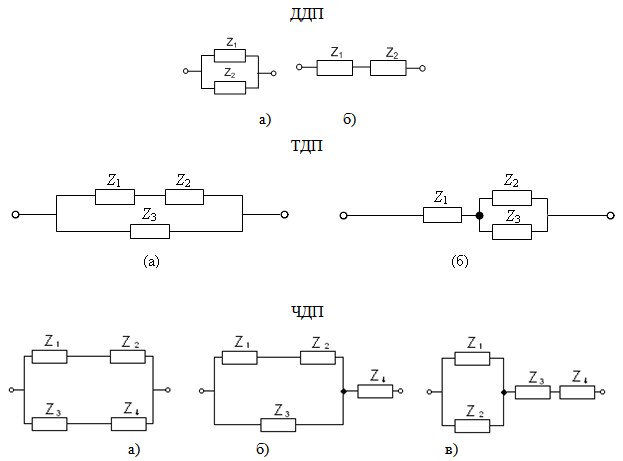
Рис 1. Топологические варианты двух- (ДДП), трёх- (ТДП) и четырёхэлементных (ЧДП) двухполюсников
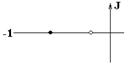
В общем случае комплексное сопротивление Zx может содержать как активное - Rx, так и реактивное Сx - ёмкостное сопротивления (независимо от характера элементов электрической цепи RX, CX заменены обобщенным параметром Zi, где i = 1,2 для ДДП, i = 1,2,3 для ТДП и i = 1,2,3,4 для ЧДП). Внешние узлы двухполюсника изображены незачерненными кружками. Недоступный внутренний узел изображен зачерненным кружком.
Из рис. 1 следует, что ДДП реализуются в двух вариантах: параллельное или последовательное соединения двух элементов Rx , Сx, отличаются отсутствием внутреннего узла. Внешние узлы ДП изображены незачернёнными кружками.
Для отдельных вариантов ДДП имеем:
а) ZХ=Z1Z2(Z1+Z2)-1;
б) ZХ=(Z1+Z2).
Из рис. 1 следует, что ТДП реализуются в двух вариантах. Это последовательное соединение двух элементов цепи с параллельным соединением третьего элемента (рисунок 1, а) и последовательное соединение первого элемента цепи с параллельным соединением двух других (рисунок 1, б).
Первый вариант (рисунок 1, а - ТДП) отличается отсутствием третьего внутреннего узла. В случае смешанного соединения элементов (рисунок 1, б - ТДП) появляется внутренний недоступный узел. Внешние узлы ДП изображены не зачернёнными кружками. Недоступный внутренний узел изображен зачернённым кружком.
Для отдельных вариантов ТДП имеем:
а) ZХ=(Z1+Z2)Z3(Z1+Z2+Z3)-1;
б)ZХ=(Z1Z2)(Z1+Z2)-1+ Z3.
Для отдельных вариантов ЧДП имеем:
а) ZХ=(Z1+Z2)(Z3+Z4)(Z1+Z2+Z3+Z4)-1;
б) ZХ=(Z1+Z2)Z3(Z1+Z2+Z3)-1+Z4;
в) ZХ=Z1Z2(Z1+Z2)-1+Z3+Z4 .
В этом случае семи вариантам обобщённых схем двухполюсников (рис. 1) соответствуют три группы вариантов использования двух- (ДДП), трёх- (ТДП), четырех- (ЧДП) элементов Rx и Сx, представленных таблицами 1, 2, 3 соответственно.
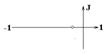
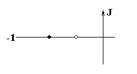
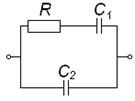
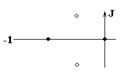
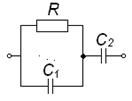
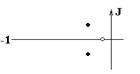
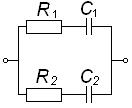
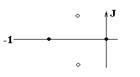
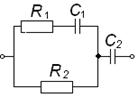
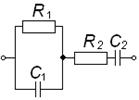
Во втором столбце таблиц представлены электрические схемы ДП, в третьем - соответствующее выражение для операторного сопротивления Zp, где p - оператор Лапласа. В четвёртом столбце таблиц - операторное сопротивление Zp в виде отношения полиномов первой или второй степеней, причем степени числителя и знаменателя либо совпадают, либо отличаются на 1. В пятом столбце таблиц приведены значения коэффициентов полиномов числителя a1, a2, a3, a4 и знаменателя b1, b2, b3, b4. В шестом столбце таблиц представлено для Zp расположение на комплексной плоскости корней уравнений числителя (в виде не зачернённых кружочков) и знаменателя (в виде зачернённых кружочков).
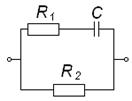
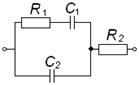
Из табл. 1 следует, что двухполюсники первой группы (ДДП) реализуются в двух вариантах: параллельное и последовательное соединения двух элементов Rx и Сx.
Табл. 1. Схемы нерезонансных ДДП с потерями
|
№ п/п. |
Электрическая схема |
Обобщенное сопротивление цепи Z(p) |
Представление Z(p) в виде отношения полиномов |
Значения коэффициентов полиномов |
Расположение полюсов и нулей Z(p) |
|
1. |
|
|
|
|
|
|
2. |
|
|
|
|
|
Из табл. 2 следует, что двухполюсники второй группы (ТДП) двухузловые ДП с параллельно-последовательным соединением трёх реализуются в четырёх вариантах попарно. Первая пара (строки 1, 2) - элементов Rx и Сx. Вторая пара (строки 3, 4) - трёхузловые ДП с параллельно-последовательным соединением трёх элементов Rx и Сx и наличием внутреннего недоступного узла.
Из табл. 3 следует, что двухполюсники третьей группы (ЧДП) реализуются в четырёх вариантах. Первый вариант (строка 1) - двухузловые ДП с параллельным соединением двух пар последовательно соединённых элементов Rx и Сx. Остальные варианты (строки 2, 3, 4) - трёхузловые ДП с параллельно-последовательным соединением четырёх элементов Rx и Сx и наличием внутреннего недоступного узла.
Табл. 2. Схемы нерезонансных ТДП с потерями
|
№ п/п. |
Электрическая схема |
Обобщенное сопротивление цепи Z(p) |
Представление Z(p) в виде отношения полиномов |
Значения коэффициентов полиномов |
Расположение полюсов и нулей Z(p) |
|
1. |
|
|
|
|
|
|
2. |
|
|
|
|
|
|
3. |
|
|
|
|
|
|
4. |
|
|
|
|
|
Табл. 3 Схемы нерезонансных ЧДП с потерями
|
№ п/п. |
Электрическая схема |
Обобщенное сопротивление цепи Z(p) |
Представление Z(p) в виде отношения полиномов |
Значения коэффициентов полиномов |
Расположение полюсов и нулей Z(p) |
|
1. |
|
|
|
|
|
|
2. |
|
|
|
||
|
3. |
|
|
|
||
|
4. |
|
|
|
Данные схемы могут быть рассмотрены как схемы замещения реальных биологических объектов.
Применение импедансного метода в оценке регенерации костной ткани при консолидации переломов и удлинении длинных трубчатых костей позволит получать своевременную, объективную информацию о локальном состоянии костной ткани и принимать адекватные действия для предотвращения осложнений.
Рецензенты:
Сиваконь С. В., д.м.н., профессор, зав. кафедрой Травматологии ортопедии и ВЭМ Медицинского института Пензенского Государственного Университета Министерства образования Российской Федерации, г. Пенза.
Моисеенко В. А., д.м.н., профессор, зав. кафедрой Травматологии и ортопедии ГБОУ ДПО «Пензенский институт усовершенствования врачей» Минздравсоцразвития Российской Федерации, г. Пенза.