В качестве матричного полимера использован линейный полиэтилен низкой плотности (ПЭНП) марки Dowlex-2032, имеющий показатель текучести расплава 2,0 г/10 мин и плотность 0,926 г/см3, что соответствует степени кристалличности 53%. В качестве нанонаполнителя использован модифицированный Na+-монтмориллонит (ММТ), полученный реакцией обмена катионов между ММТ и ионами четвертичного аммония [4].
Нанокомпозиты полиэтилен низкой плотности/монтмориллонит (ПЭНП/ММТ) приготовлены смешиванием компонентов в расплаве с использованием двухшнекового экструдера Haake при температуре 473 К [4].
Образцы для испытаний на растяжение получены инжекционным литьем на литьевой машине Arburg Allrounder 305-210-700 при температуре 463 К и давлении 35 бар. Испытания на растяжение выполнены на приборе Instron модели 1137 с непосредственным получением цифровых данных при температуре 293 К и скорости деформации ~ 3,35´10-3 с-1. Средняя погрешность определения модуля упругости составляла 7%, предела текучести - 2% [4].
Коэффициент газопроницаемости измерен на пленочных образцах нанокомпозитов, полученных прессованием под давлением, которые имели толщину 150 мкм. Коэффициенты газопроницаемости по кислороду (О2), азоту (N2) и двуокиси углерода (СО2) измерены при температуре 308 К методом переменного объема при постоянном давлении [4].
Основное уравнение фрактальной модели процессов газопереноса имеет вид [9]:
![]() , (1)
, (1)
где Р0 - константа, fc - относительный флуктуационный свободный объем, dh и dм - диаметры микрополости свободного объема и молекулы газа-пенетранта, соответственно, Dn - размерность структуры, контролирующая процессы газопереноса, ds - спектральная размерность, принимаемая для линейного ПЭНП равной 1,0 [10].
Из уравнения (1) следует, что построение зависимости Р(1/dм) при dh=const и ds=const должно дать линейную корреляцию, из наклона которой можно определить величину показателя 2(Dn-ds)/ds в уравнении (1) и, следовательно, размерность Dn. Как показано ранее [9], для полимерных материалов могут быть реализованы два механизма газопереноса: структурный или молекулярный в зависимости от величины отношения (dh/dм). При (dh/dм)>1,7 взаимодействие молекул газа-пенетранта и стенок микрополости свободного объема отсутствует, и в этом случае величина Dn принимается равной фрактальной (хаусдорфовой) размерности структуры df. При (dh/dм)≤1,7 молекула газа-пенетранта взаимодействует со стенками указанных микрополостей, чья размерность примерно равна размерности областей локализации избыточной энергии Df и тогда Dn=Df. Очевидно, что для первого механизма существует общее для всех фрактальных объектов ограничение: df≤d, где d - размерность евклидова пространства, в котором рассматривается фрактал (в нашем случае d=3).
Объемную долю нанонаполнителя φн определяли согласно известному уравнению [11]:
![]() , (2)
, (2)
где Wн - массовое содержание нанонаполнителя, ρн - плотность монтмориллонита, примерно равная 2000 кг/м3 [4].
Построение указанных выше зависимостей Р(1/dм) для исходного ПЭНП и нанокомпозитов ПЭНП/ММТ с содержанием ММТ φн=0,005, 0,015, 0,025 и 0,035 приведено на рис. 1, откуда следует, что эти зависимости действительно линейны, их наклон для пяти исследуемых материалов (включая матричный ПЭНП) одинаков и величина Dn≈8,7. Исходя из сказанного выше, следует принять Dn=Df. Как известно [12], размерности Df и df связаны между собой соотношением:
![]() . (3)
. (3)
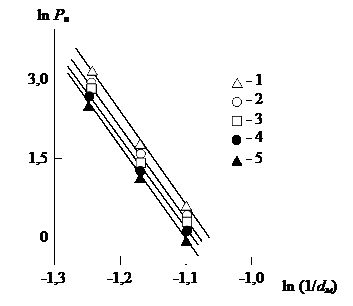
Рис. 1. Зависимости коэффициента газопроницаемости Рн от обратной величины диаметра молекулы газа-пенетранта dм в двойных логарифмических координатах для матричного ПЭНП (1) и нанокомпозитов ПЭНП/ММТ с объемным содержанием нанонаполнителя 0,005 (2), 0,015 (3), 0,025 (4) и 0,035 (5).
Из уравнения (3) следует, что df=2,87=const. Оценить величину df структуры исследуемых нанокомпозитов можно еще одним способом, а именно применением уравнения [12]:
![]() ,(4)
,(4)
где ν - коэффициент Пуассона, оцениваемый по результатам механических испытаний с помощью соотношения [13]:
![]() , (5)
, (5)
где σТ - предел текучести, Ен - модуль упругости нанокомпозита.
Расчет согласно уравнению (4) показал, что величина df для исследуемых нанокомпозитов варьируется в пределах 2,558-2,730 и это согласно уравнению (3) соответствует Df=3,36-4,70. Полученные таким образом значения Df существенно ниже соответствующей размерности, оцененной из графиков рис. 1 (Df≈8,7). Это расхождение обусловлено мультифрактальной природой структуры полимерной матрицы исследуемых нанокомпозитов. Как известно [9; 11], указанная структура описывается классической куполообразной мультифрактальной диаграммой (df-2)(dh), где dh - диаметр микрополости свободного объема. В процессах переноса задействованы только те микрополости, которые отвечают условию dh≥dм. Поэтому размерность df доступной для переноса части полимерной матрицы будет больше, чем ее усредненная величина, полученная согласно уравнению (4). Такое же утверждение справедливо и для размерности Df (уравнение (3)).
Ранее было показано [14], что величину Р для аморфно-кристаллического полимера можно записать так:
![]() ,(6)
,(6)
где Р - коэффициент газопроницаемости для полностью аморфного полимера, t - коэффициент извилистости, обусловленный сложностью путей переноса газов между кристаллитами и зависящий не только от степени кристалличности К, но и от величины формы и распределения кристаллитов (и частиц нанонаполнителя в рассматриваемом случае) по размерам, b - коэффициент неподвижности цепей, зависящий от уровня молекулярной подвижности и предполагаемый постоянным в силу условия df=const.
В работе [9] было показано, что в рамках мультифрактальной модели процессов газопереноса величина t определяется так:
![]() , (7)
, (7)
где ![]() - доступная для диффузии газа с диаметром молекулы dм часть аморфной фазы αам, равная [9]:
- доступная для диффузии газа с диаметром молекулы dм часть аморфной фазы αам, равная [9]:
![]() . (8)
. (8)
Значения dм для исследуемых газов приведены в работе [15]. Отметим, что при относительной доле аморфной фазы αам=0,47 ее доступная для процессов переноса часть ![]() , отвечающая условию dh≥dм, варьируется в пределах 0,043-0,112, т.е. существенно меньше и соответствует критерию df≥2,87. Величину αам в случае исследуемых нанокомпозитов можно определить следующим образом. Предполагается, что кристаллиты, нанонаполнитель и плотноупакованные на поверхности слоевого интеркалированного ММТ межфазные области с относительной долей φмф непроницаемы для диффузии, и в этом случае:
, отвечающая условию dh≥dм, варьируется в пределах 0,043-0,112, т.е. существенно меньше и соответствует критерию df≥2,87. Величину αам в случае исследуемых нанокомпозитов можно определить следующим образом. Предполагается, что кристаллиты, нанонаполнитель и плотноупакованные на поверхности слоевого интеркалированного ММТ межфазные области с относительной долей φмф непроницаемы для диффузии, и в этом случае:
![]() .(9)
.(9)
Соотношение между φмф и φн для интеркалированного ММТ имеет вид [11]:
![]() . (10)
. (10)
Тогда теоретический коэффициент газопроницаемости нанокомпозитов ![]() можно определить согласно уравнению [9]:
можно определить согласно уравнению [9]:
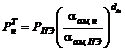 ,(11)
,(11)
где РПЭ - коэффициент газопроницаемости матричного полимера (ПЭНП) по данному газу, αам, н и αам, ПЭ - относительные доли аморфной фазы для нанокомпозитов ПЭНП/ММТ и матричного ПЭНП, соответственно.
На рис. 2 приведено сравнение полученных экспериментально Рн и рассчитанных согласно уравнению (11) коэффициентов газопроницаемости для исследуемых нанокомпозитов ПЭНП/ММТ по трем газам (О2, N2 и СО2). Как можно видеть, получено превосходное соответствие теории и эксперимента (среднее расхождение Рн и ![]() составляет ~ 5,5%, что существенно ниже погрешности эксперимента при определении коэффициента газопроницаемости [16]), которое подтверждает корректность предложенной мультифрактальной модели.
составляет ~ 5,5%, что существенно ниже погрешности эксперимента при определении коэффициента газопроницаемости [16]), которое подтверждает корректность предложенной мультифрактальной модели.
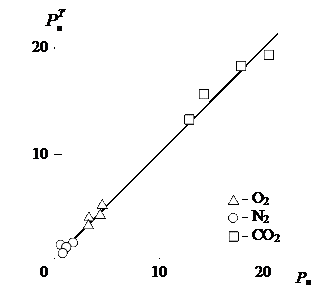
Рис. 2. Сравнение экспериментальных Рн и рассчитанных согласно уравнению (11) ![]() величин коэффициента газопроницаемости по О2 (1), N2 (2) и СО2 (3) для нанокомпозитов ПЭНП/ММТ. Величины Р даны в единицах Баррера: 10-10 см3×см/(см2×с×см.ртутн.столба).
величин коэффициента газопроницаемости по О2 (1), N2 (2) и СО2 (3) для нанокомпозитов ПЭНП/ММТ. Величины Р даны в единицах Баррера: 10-10 см3×см/(см2×с×см.ртутн.столба).
Таким образом, предложенная мультифрактальная модель позволяет корректное количественное теоретическое описание снижения коэффициента газопроницаемости нанокомпозитов ПЭНП/ММТ по мере увеличения содержания нанонаполнителя при учете роли межфазных областей в наблюдаемом эффекте. Рассмотрена структурная трактовка коэффициента извилистости. Теоретические оценки подтвердили как мультифрактальную природу структуры полимерной матрицы нанокомпозитов, так и интеркаляцию слоевого нанонаполнителя.
Рецензенты:
- Алоев В.З., д.х.н., профессор, зав. кафедрой физики Кабардино-Балкарской государственной сельскохозяйственной академии Департамента научно-технической политики Министерства образования и науки РФ, г. Нальчик.
- Шогенов В.Н., д.ф.-м.н., заместитель директора по науке Учреждения Российской академии наук Института экологии горных территорий КБНЦ РАН, г. Нальчик.
Работа получена 13.12.2011



