В курсах физики утверждается, что если тело массы ![]() равномерно поднимать вверх на высоту
равномерно поднимать вверх на высоту ![]() с помощью силы
с помощью силы ![]() , то сила совершает работу
, то сила совершает работу ![]() , равную потенциальной энергии
, равную потенциальной энергии ![]() , а сила тяжести отрицательную работу
, а сила тяжести отрицательную работу ![]() [1]. Автором [2] было показано, что работа подъема тела на высоту
[1]. Автором [2] было показано, что работа подъема тела на высоту ![]() всегда больше
всегда больше ![]() . Чтобы поднимать тело вверх, необходимо приложить силу
. Чтобы поднимать тело вверх, необходимо приложить силу ![]() . Работа подъема будет равна
. Работа подъема будет равна
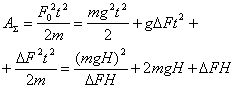 (1)
(1)
Время подъема ![]() найдется из соотношения:
найдется из соотношения: ![]() . На графике (рис. 1) показана зависимость работы
. На графике (рис. 1) показана зависимость работы ![]() , выраженной в долях
, выраженной в долях ![]() , от величины соотношения
, от величины соотношения ![]() . Работа имеет минимум, равный
. Работа имеет минимум, равный ![]() при
при ![]() . При свободном падении тела с высоты
. При свободном падении тела с высоты ![]() потенциальная энергия переходит в кинетическую
потенциальная энергия переходит в кинетическую ![]() , где
, где ![]() .
.
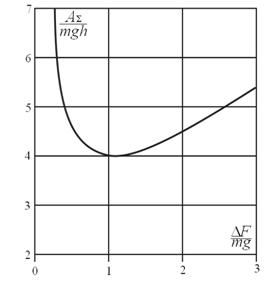
Рисунок 1. Зависимость работы ![]() , выраженной в долях
, выраженной в долях ![]() , от величины соотношения
, от величины соотношения ![]()
Таким образом, потенциальная энергия соответствует только работе, совершаемой силой тяжести при СВОБОДНОМ падении тела. Работа при свободном падении:
![]() (a)
(a)
![]() (b) (2)
(b) (2)
Т.к. ![]() , а
, а ![]() ,
, ![]() -импульс силы тяжести.
-импульс силы тяжести.
Рассмотрим работу, совершаемую силой тяжести, при других случаях падения тел.
СЛУЧАЙ I. Падение происходит при действии постоянной силы ![]() , направленной вертикально. Если сила направлена вниз (
, направленной вертикально. Если сила направлена вниз (![]() ), как сила тяжести, то это движение можно рассматривать как свободное падение под действием силы
), как сила тяжести, то это движение можно рассматривать как свободное падение под действием силы ![]() , как в гравитационном поле напряженности
, как в гравитационном поле напряженности ![]() . Примем следующие числовые значения:
. Примем следующие числовые значения: ![]() кг,
кг, ![]() м,
м, ![]() м/с2,
м/с2, ![]() Н. Получаем: время падения
Н. Получаем: время падения ![]() с2, скорость
с2, скорость ![]() (м/с)2,
(м/с)2, ![]() Дж, работа
Дж, работа ![]() Дж.
Дж.
Таким образом, работа падения не равна потенциальной энергии ![]() Дж (при обычном свободном падении
Дж (при обычном свободном падении ![]() с2,
с2, ![]() (м/с)2,
(м/с)2, ![]() Дж).
Дж).
Если сила направлена вертикально вверх (![]() ), то она является силой сопротивления (трения). В этом случае падение происходит под действием результирующей силы:
), то она является силой сопротивления (трения). В этом случае падение происходит под действием результирующей силы:
![]() Н
Н
с ускорением: ![]() м/с2.
м/с2.
Время падения: ![]() с2, скорость
с2, скорость ![]() (м/с)2,
(м/с)2, ![]() Дж. Используя обычную формулу (2a) для расчета работы, получаем:
Дж. Используя обычную формулу (2a) для расчета работы, получаем: ![]() Дж. Используя формулу (2b), имеем
Дж. Используя формулу (2b), имеем ![]() Дж.
Дж.
Автором в работах [3, 4,5] показано, что работа силы (производство энергии) пропорциональна квадрату импульса силы:
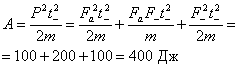
Это говорит о том, что в общем случае работа зависит от времени действия силы, а не от пути, т.к. один и тот же путь (в данном случае ![]() м) может быть пройден за разное время в зависимости от величины силы сопротивления. Время падения:
м) может быть пройден за разное время в зависимости от величины силы сопротивления. Время падения: ![]() , работа
, работа ![]() . Из этих выражений могут быть составлены безразмерные комплексы
. Из этих выражений могут быть составлены безразмерные комплексы
![]() (а)
(а)
![]() (b) (3)
(b) (3)
Где ![]() может изменяться от 0 до 1. Случай
может изменяться от 0 до 1. Случай ![]() соответствует условию левитации тела, когда оно неподвижно зависает под действием двух одинаковых, но противоположно направленных сил
соответствует условию левитации тела, когда оно неподвижно зависает под действием двух одинаковых, но противоположно направленных сил ![]() . На графике (рис. 2) показана зависимость комплекса
. На графике (рис. 2) показана зависимость комплекса ![]() в зависимости от величины
в зависимости от величины ![]() .
.
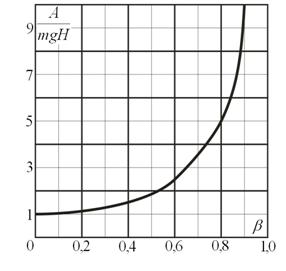
Рисунок 2. Показана зависимость комплекса ![]() в зависимости от величины
в зависимости от величины ![]()
Таким образом, в случае действия постоянной силы сопротивления (трения), работа, совершаемая силой тяжести ![]() , возрастает и в пределе
, возрастает и в пределе ![]() при
при ![]() . Случай
. Случай ![]() соответствует статической задаче, когда груз удерживается подвесом на неизменной высоте
соответствует статической задаче, когда груз удерживается подвесом на неизменной высоте ![]() .
.
СЛУЧАЙ II. Падение происходит при действии силы сопротивления, пропорциональной скорости падения:
![]() (4)
(4)
Решение этого дифференциального уравнения при нулевых начальных условиях имеет вид:
![]() (а)
(а)
![]() (b) (5)
(b) (5)
![]() (6)
(6)
Если использовать общепринятую формулу ![]() , то получаем
, то получаем ![]() Дж. Примем
Дж. Примем ![]() Н·с/м. Расчет по формуле
Н·с/м. Расчет по формуле ![]() при
при ![]() с (время определяется из трансцендентного уравнения (6) при
с (время определяется из трансцендентного уравнения (6) при ![]() ) дает численное значение работы
) дает численное значение работы ![]() Дж. Силу
Дж. Силу ![]() можно представить в виде суммы двух сил:
можно представить в виде суммы двух сил: ![]() , где
, где ![]() - сила, вызывающая ускоренное движение тела вниз в соответствии со II законом Ньютона, ускорение определяется выражением (5b), а сила
- сила, вызывающая ускоренное движение тела вниз в соответствии со II законом Ньютона, ускорение определяется выражением (5b), а сила ![]() – сила сопротивления, скорость определяется выражением (5a).
– сила сопротивления, скорость определяется выражением (5a).
Используя импульсы сил ![]() , работу, совершаемую силой тяжести, можно расписать более подробно
, работу, совершаемую силой тяжести, можно расписать более подробно
![]() (7)
(7)
Импульс силы, вызывающей ускоренное движение тела:
![]() (8)
(8)
При ![]() с
с ![]() Н·с;
Н·с; ![]() Дж.
Дж.
Импульс силы трения:
![]() (9)
(9)
При ![]() с
с ![]() Н·с;
Н·с; ![]() Дж.
Дж.
Работа, связанная с трением при УСКОРЕННОМ движении:
![]() Дж
Дж
Суммарная работа ![]() Дж
Дж
Таким образом, работа совершаемая силой тяжести при падении тел, зависит от силы сопротивления среды. Чем больше сила сопротивления, тем больше время падения и больше импульс силы тяжести, а работа, совершаемая силой, пропорциональна квадрату импульса силы: 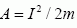 .
.
СПИСОК ЛИТЕРАТУРЫ
1. Кикоин И.К., Кикоин А.К. Физика: Учебн. для 9 кл. средн. шк. – М.: Просвещение, 1990.
2. Иванов Е.М. Работа и энергия в классической механике и первый закон термодинамики. Димитровград: ДИТУД УлГТУ, 2005.
3. Иванов Е.М. Определение работы и работа силы трения. //Успехи современного естествознания. 2005. №8. С.10
4. Иванов Е.М. Работа при движении тел с трением. //Фундаментальные исследования. 2005. №6. С.10
5. Иванов Е.М. Работа в классической механике. //Современные наукоемкие технологии. 2005. №5 С. 12.



