Введение
Распространение и развитие информационных технологий и компьютерной техники в различных сферах деятельности человека, становление информационного общества и формирование национальной цифровой экономики обусловливают возрастающую потребность в специалистах в области информационных технологий, что отражено в Стратегии развития информационного общества в Российской Федерации на 2017–2030 годы [1]. При недостатке в стране квалифицированных сотрудников ИT-отрасли, ориентированных на планирование, разработку, интеграцию, эксплуатацию и поддержку информационных систем, подготовке таких специалистов уделяется особое внимание.
Согласно Федеральным государственным образовательным стандартам высшего образования, студенты укрупненной группы «Информатика и вычислительная техника» готовятся, в том числе, к решению задач профессиональной деятельности проектного типа, что требует формирования компетенций, связанных со способностями выпускников к системному и критическому мышлению, к самоорганизации и самообучению, к работе в команде, к разработке и реализации проектов [2]. Обучение математике в вузе способствует формированию и развитию перечисленных способностей, а математическая составляющая является неотъемлемой частью профессиональной деятельности ИТ-специалистов и связана с ее спецификой, в связи с чем актуален вопрос качества математической подготовки студентов.
Цель исследования состоит в конкретизации и описании организационно-педагогических условий, создание которых в процессе обучения студентов математике способствует повышению качества математической подготовки будущих специалистов в области информационных технологий.
Материалы и методы исследования
Работа опирается на методы анализа, синтеза и обобщения исследований по рассматриваемому вопросу; проектирование процесса обучения, мониторинг его результатов и обработку полученных данных; ориентирована на требования и рекомендации к результату подготовки специалистов в области информационных технологий, отраженных в нормативных документах. Применение обозначенных методов позволило определить ключевые аспекты в обучении математике студентов и сформулировать их в виде организационно-педагогических условий, ориентированных на повышение качества математической подготовки будущих ИТ-специалистов. В основе исследования лежат положения деятельностного, контекстного и личностно-ориентированного подходов: обучение математике студентов описано в условиях вовлечения их в деятельность по решению задач с учетом способностей и потребностей обучающихся в единстве целей, содержания, методов и средств обучения.
В работе рассмотрено обучение студентов СибГУ им. М.Ф. Решетнева направлений подготовки 09.03.01 Информатика и вычислительная техника направленности «Программное обеспечение мобильных систем и приложений» и 09.03.04 Программная инженерия направленности «Разработка и сопровождение информационных систем и web-приложений» с позиции математической подготовки будущих выпускников. Согласно учебным планам перечисленных направлений подготовки, студентам необходимо освоить несколько дисциплин математического цикла, в том числе дисциплины, реализуемые кафедрой высшей математики: «Алгебра и аналитическая геометрия», «Математический анализ», «Теория вероятностей и математическая статистика». В работе рассмотрено обучение математике студентов младших курсов в рамках перечисленных дисциплин.
Результаты исследования и их обсуждение
С опорой на работу Е.В. Полонского, в которой качество математической подготовки студентов определяется как уровень достижения целей обучения математике и степень соответствия результата обучения ожиданиям студентов и запросам общества [3, с. 2737], рассмотрено повышение качества математической подготовки студентов в контексте достижения целей и получения результатов обучения на более высоком уровне при активной деятельности мотивированных на приобретение знаний студентов.
Формирование обозначенных в образовательных стандартах компетенций, а значит, и развитие у студентов способности к проектной деятельности при использовании математического аппарата, сопряжено с достижением в процессе обучения математике следующих результатов: развитие внутренней мотивации студентов к изучению математики, приобретение фундаментальных математических знаний; установление внутрипредметных и межпредметных связей; усвоение математических методов и формирование готовности к их применению; развитие способности к анализу и синтезу информации, к самообучению, к интеграции информационных технологий и математики, к применению математического аппарата для решения задач будущей профессиональной деятельности и получения конечного продукта. Перечисленные результаты сформулированы в общем виде и для оценивания требуют содержательной конкретизации к каждой теме. Полученная студентами по пятибалльной шкале оценка свидетельствует об уровне достижения результатов обучения, а значит, и о качестве математической подготовки студентов: «отлично» – высокий уровень, «хорошо» – уровень выше среднего; «удовлетворительно» – средний уровень.
Достижению планируемых результатов на более высоком уровне способствует создание дополняющих друг друга организационно-педагогических условий.
Условие 1. Вовлечение студентов в проектную деятельность при обучении математике.
Согласно распространенной точке зрения, метод проектов ориентирован на самостоятельную деятельность обучающихся по решению значимой проблемы или задачи с целью получения результата при использовании исследовательских методов [4, с. 59]. Разработка и реализация проекта в большинстве случаев предполагают проведение исследования, а проектирование в процессе обучения математике будущих специалистов ИТ-сферы – трудоемкий процесс, требующий дополнительных временных затрат. Проектные задания, сформулированные преподавателем или студентами, позволяют выявить обучающихся, ориентированных на участие в проектной деятельности, и предоставляют им такую возможность. В современных исследованиях экспериментально подтверждено, что выполнение проекта способствует развитию у студентов способности к самообучению, анализу и систематизации больших объемов информации, самостоятельному принятию решений, а исследовательская работа в процессе обучения позволяет охватить больший объем информации за счет своей интенсивности [5].
Вовлечение студентов в проектную деятельность требует от преподавателя подбора специального содержания и организации самостоятельной работы студентов, что отражено в условиях, сформулированных далее.
Условие 2. Прикладная направленность содержательного наполнения дисциплин математического цикла и применение информационных технологий при выполнении заданий.
Прикладная направленность содержания не только демонстрирует значимость математического аппарата для решения конкретных задач, но и помогает студентам определиться с возможными дальнейшими направлениями деятельности. Так, студент может предложить авторское решение рассматриваемой прикладной задачи, расширить задачу, предложить тему исследования самостоятельно. Многообразие прикладных задач служит студентам базой для поиска и самостоятельного формулирования тем проектных работ.
При подборе задач и составлении заданий важно предусмотреть возможность, а в некоторых случаях и необходимость, применения информационных технологий при их решении. В работе Н.Н. Яремко и Н.Н. Авксентьевой подтверждено, что ориентированность процесса математической подготовки будущих ИТ-специалистов на использование информационных технологий, цифровых средств и визуализацию способствует самообразованию и повышает учебно-познавательную мотивацию [6]. Подбору и корректировке содержания математических и информационных дисциплин помогают выделенные в работе Ю.Б. Мельникова, Е.А. Онохиной и А.В. Лаптевой ключевые направления интеграции математики и информационных технологий, в том числе: интеграция методов и понятий; использование информационных технологий в обогащении математического аппарата, применение математической модели как основы компьютерной модели и ее описания [7]. Интеграции дисциплин математического цикла и информационных технологий способствует выполнение студентами заданий повышенной сложности различных контекстов, которые могут быть расширены до проектных работ исследовательского типа с представлением полученных результатов на занятиях-конференциях и студенческих конференциях в форме докладов, публикацией результатов в сборниках студенческих работ различного уровня.
В рамках представленного исследования студентами экспериментальной группы в процессе обучения математике выполнялись подобные работы, перечислим некоторые темы: «Компьютерное моделирование задачи Дидоны»; «Графический анализ частных решений задач механики», «Задача о падении тела с учетом сопротивления воздуха»; «Нахождение матричной экспоненты методами линейной алгебры». При выполнении каждой из работ студенты либо представляли графическую динамическую модель решения задачи и проводили анализ этой модели при различных значениях изменяющихся параметров, либо разрабатывали алгоритм решения задачи и составляли авторскую программу, его реализующую.
В целом, предлагаемые студентам учебные задания прикладной направленности способствуют вовлечению заинтересованных и одаренных студентов в проектную деятельность по решению более сложных задач. Например, при изучении теории вероятностей требуется сформировать в представлении студентов понимание статистической природы вероятности некоторого события. Добиться этого помогает статистическое моделирование, реализуемое путем написания компьютерных программ, имитирующих традиционно рассматриваемые в теории вероятностей серии экспериментов. Студентам предлагается разноуровневое задание по теме: «Компьютерное моделирование опытов с бросанием монет». На первом этапе выполнения задания рассматривается опыт с бросанием одной симметричной монеты. Здесь студенты пишут программу, генерирующую случайным образом n раз числа 0 и 1 («орел» и «решка») и выводящую на экран относительную частоту их появления. Реализуя эксперимент с бросанием монеты и анализируя результат, студенты должны сделать вывод о процессе приближения относительной частоты к теоретической вероятности. На втором этапе заинтересованные студенты моделируют эксперимент с бросанием двух монет. Анализ этих экспериментов принципиально отличается. Первая компьютерная модель позволяет проверить равновозможность выпадения «орла» и «решки», а вторая модель, опираясь на предположение о равновозможности выпадения «орла» и «решки», проверяет равновозможность всех исходов эксперимента. На третьем этапе более подготовленные и мотивированные студенты строят модель эксперимента с бросанием любого числа монет [8].
Условие 3. Индивидуализация процесса обучения и вовлечение обучающихся в самостоятельную работу по приобретению фундаментальных математических знаний.
Сокращение аудиторных часов и увеличение объема учебного материала требуют от обучающихся дополнительных временных затрат и поиска новой информации, что сопряжено с вовлечением студентов в индивидуальную самостоятельную работу. При этом ценен опыт самообразовательной деятельности студентов, который в дальнейшем полезен при решении нестандартных задач. За счет имеющейся возможности при самостоятельной работе осваивать учебный материал в своем темпе и выбирать для выполнения задания различного уровня сложности реализуется индивидуализация обучения.
В связи с возрастающей ролью самостоятельной работы в процессе математической подготовки необходимо обратить особое внимание на ее организацию.
Условие 4. Организация смешанного обучения математике с применением электронных образовательных ресурсов.
Дополнение традиционных лекционных и практических занятий электронным обучением математике посредством авторских образовательных ресурсов по математическим дисциплинам позволяет организовать управляемую и корректируемую как преподавателем, так и самими студентами самостоятельную работу обучающихся посредством разнообразных заданий. Т.В. Атяскиной и В.В. Кузнецовым разработана модель формирования различных групп умений самообразования будущих специалистов в условиях электронных образовательных ресурсов на основе специально разработанных заданий, активизирующих самостоятельный поиск оптимальных способов деятельности [9]. Дополнение прикладных задач вопросами и заданиями, активизирующими познавательную активность обучающихся, помогает вовлечению студентов в самостоятельную работу.
В рамках представленного исследования разработаны электронные образовательные ресурсы в среде LMS Moodle по дисциплинам: «Алгебра и аналитическая геометрия», «Математический анализ», «Теория вероятностей и математическая статистика», использование которых результативно в организации самостоятельной работы обучающихся за счет структуры, содержательного разноуровневого наполнения и оценочных средств, единой стилистики и схожего интерфейса, наличия рекомендаций к использованию ресурсов. Взаимосвязанное содержательное наполнение трех ресурсов является их особенностью. При использовании образовательных ресурсов студенты получают возможность изучать теоретический материал и методы решения различных задач, выполнять самоконтроль, получать консультации, взаимодействовать с одногруппниками, что в дальнейшем позволяет найти ответы на вопросы, возникающие при выполнении проектных заданий. Электронные образовательные ресурсы постоянно корректируются содержательно и структурно, с учетом запросов студентов и изменяющихся нормативных требований.
Пятое и шестое условия связаны с активностью участников образовательного процесса и дополняют предыдущие условия.
Условие 5. Активность студентов и их готовность работать в команде, наличие лидера. Мотивация на достижение успеха в деятельности.
Многолетние наблюдения свидетельствуют о том, что от активности и ответственности актива группы, личного примера лидеров группы во многом зависят активность и успеваемость группы в целом: помогают отлаженная организационная работа лидеров группы, своевременное и продуктивное взаимодействие с дирекциями, преподавателями, внутри группы. В работе В.В. Таракановой, Н.Г. Соловьевой, Е.В. Ахмедовой описаны функции актива группы в создании сплоченного коллектива, мотивированного на приобретение знаний путем формирования дружеской атмосферы в группе, организации дополнительных занятий и мероприятий, предоставления информации об учебных ресурсах и материалах, адаптации новых студентов к процессу обучения, решения проблем [10, с. 25]. При изучении математических дисциплин на сплоченность группы влияют, в том числе, коллективное обсуждение темы, выполнение групповых заданий, участие в деловых играх.
Условие 6. Межкафедральное взаимодействие, непрерывность и преемственность в обучении математике [11].
Не все дисциплины математического цикла реализуются кафедрой высшей математики, большинство дисциплин реализуются специальными кафедрами, в связи с чем актуален вопрос межкафедральной интеграции, что позволяет при обучении математике оптимально подобрать учебный материал и построить логику его изложения, избежать забывания ранее полученных знаний и продемонстрировать их прикладной аспект.
Реализация перечисленных условий в комплексе способствует повышению качества математической подготовки студентов, что подтверждается экспериментально. В эксперименте на протяжении трех лет участвовали студенты двух групп (по 25 обучающихся в каждой группе). В экспериментальной группе при обучении математическим дисциплинам созданы предложенные условия. Мониторинг (входной, текущий и итоговый) [12] результатов обучения математике позволяет сформулировать следующие выводы.
Во-первых, результаты входного мониторинга (тестирование студентов, анализ баллов единого государственного экзамена по математике) для контрольной и экспериментальной групп свидетельствуют о сопоставимых стартовых возможностях обучающихся в группах.
Во-вторых, электронные образовательные ресурсы играют важную роль в проведении текущего мониторинга образовательных результатов и обработке полученных данных. Для систематического отслеживания сформированности результатов обучения в рамках электронных образовательных ресурсов предусмотрены обучающие тесты с комментариями по итогам изучения материала для каждого лекционного и практического занятий, итоговые тесты по темам и разделам. Тестовые задания предшествуют более сложным задачам или являются их частями. Диагностические мероприятия в электронной среде дополняют аудиторные контрольные работы и собеседования по выполненным индивидуальным заданиям, с занесением полученных баллов в электронный журнал оценок. Рейтинговые баллы, которые переводятся в пятибалльные оценки, свидетельствующие об уровне математической подготовки студента, складываются из баллов, полученных при выполнении тестовых заданий электронного образовательного ресурса; баллов, выставленных преподавателем по итогам контрольных работ и защиты индивидуальных заданий; поощрительных баллов, получаемых за особые достижения, например за участие в конференциях, активность на занятиях. Текущий мониторинг позволяет преподавателю и обучающемуся отследить уровень усвоения студентами учебного материала в динамике и скорректировать учебный процесс при необходимости.
При анализе успеваемости студентов экспериментальной и контрольной групп по итогам обучения математике (Рис.) получены средние балльные оценки по математическим дисциплинам в группах, которые позволяют констатировать увеличение среднего балла в экспериментальной группе по итогам обучения математическим дисциплинам.
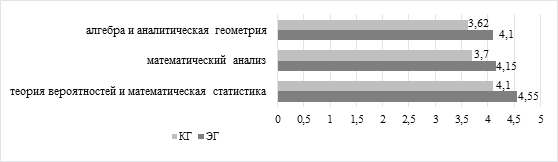
Рис. Средний балл студентов по математическим дисциплинам в экспериментальной и контрольной группах
В-третьих, при проведении итогового мониторинга, при анализе учебных планов определены дисциплины («Физика»; «Дискретная математика»; «Математические основы искусственного интеллекта»; «Математическая логика»; «Основы математического программирования»; «Методы математического моделирования»), обучение которым опирается на изученный ранее математический аппарат. По итогам промежуточной аттестации студентов средний балл по этим дисциплинам в экспериментальной группе выше. Анализ индивидуальных достижений студентов на протяжении всего срока обучения показывает, что обучающиеся, вовлеченные при изучении математики в выполнение проектных заданий, в основном продолжают начатую работу и наиболее успешны на старших курсах.
О положительном влиянии создания описанных условий свидетельствуют ответы студентов при анкетировании и отзывы преподавателей. Студенты отмечают повышение интереса к изучению математики за счет решения задач прикладной направленности и демонстрации возможностей применения математического аппарата; ценность приобретения опыта решения таких задач. Преподаватели смежных дисциплин отмечают осознание студентами необходимости применения полученных ранее математических знаний и возросшее число попыток к их применению.
Заключение
Анализ полученных в исследовании результатов позволяет сформулировать вывод о том, что создание предложенных организационно-педагогических условий в комплексе способствует повышению качества математической подготовки студентов информационных направлений подготовки. Экспериментально подтверждено, что повышению качества математической подготовки студентов информационных направлений подготовки способствует развитие у студентов способности к проектированию и проведению исследования путем их вовлечения в решение задач прикладной направленности в процессе обучения математике. При организации процесса обучения важно учитывать, что решение подобных задач и усвоение студентами необходимых фундаментальных математических знаний, методов и способов деятельности сопряжены с индивидуализацией обучения и вовлечением студентов в управляемую самостоятельную работу в формате электронных образовательных ресурсов, мониторингом и корректировкой процесса обучения, при активном взаимодействии студентов и преподавателей разных кафедр, лидерстве студентов.



