Опыт работы показывает, что часто сложный вид уравнения пугает школьников, и многие из них даже не приступают к решению, те же, кто всё-таки приступил к решению, пытаются безуспешно использовать известные методы решения без учета анализа самого уравнения. Ознакомление обучающихся с некоторыми методическими рекомендациями позволит избежать этой проблемы и вооружит их определенными приемами решения нестандартных уравнений.
Цель исследования – разработка методических рекомендаций по обучению учащихся поиску решения нестандартных уравнений.
Материал и методы исследования. Методы исследования носили комплексный характер, среди них выделялись теоретические методы: анализ научно-методических статей и учебных пособий, анализ учебников и задачников по алгебре, алгебре и началам анализа и эмпирические методы: анкетирование школьников и учителей математики, наблюдение за процессом поиска решения нестандартных уравнений, а также педагогический эксперимент.
Проведенный анализ показал, что существует ряд исследований, посвященных обучению решению нестандартных уравнений (Ю.М. Колягин, И.Ф. Шарыгин, В.И. Голубев, Г.В.Дорофеев, Г.К. Муравин, А.Г. Мерзляк, О.Ю. Черкасов, А.Г. Якушев и др.). Однако проблема обучения поиску решения нестандартных уравнений в научно-методической и учебной литературе не достаточно разработана. Многочисленные задачники [1-3] содержат различные примеры решения нестандартных уравнений без подробного их анализа и методических рекомендаций по организации поиска их решения.
Одна из важных рекомендаций методистов [4-6] при решении задач: прежде чем приступить к решению задачи, следует начать с анализа данных, представленных в этой задаче. Не является исключением и процесс поиска решения нестандартных уравнений. Если стандартные уравнения еще допускают поспешных действий, то при решении нестандартных уравнений такая спешка ни к чему хорошему не приведет. Необходимы не только стандартные, но и нестандартные приемы решения уравнений.
Анализ литературы показал, что под нестандартным приемом решения уравнений в методической литературе [7; 8] понимают прием решения уравнений, в котором основную роль при переходе к равносильным уравнениям и неравенствам играют свойства функций (монотонность, четность, нечетность, периодичность и др.). Л.К.Садыкова [9], Л.С. Капкаева [10] выделяют функциональные приемы решения уравнений и неравенств, знакомство с которыми позволит учащимся быть более успешными при решении нестандартных уравнений.
Приведем материалы выступления автора статьи перед учителями и учащимися 10-11 классов на семинаре по подготовке к ЕГЭ, некоторые рекомендации приведены автором в статье [5, с. 214].
· Решить уравнение: 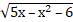 +
+ 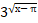 =
= 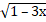 .
.
Как видим, в уравнении участвуют три различные функции. Применение известных методов не позволило школьникам найти решение самостоятельно. Действия тех, кто приступил к решению, сводились только к возведению обеих частей уравнения в квадрат, что, конечно, ни к чему хорошему не привело. Наличие показательной функции не позволяет упростить уравнение возведением в квадрат. И только с помощью наводящих вопросов, организованных в ходе поиска решения уравнения и анализа его данных, некоторые обучающиеся начали выделять функции, входящие в него, и обдумывать условия существования решения уравнения, т.е. приступили к анализу области определения.
После нахождения области определения обучающиеся выяснили:
а)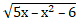 существует при х, принадлежащих промежутку [2; 3];
существует при х, принадлежащих промежутку [2; 3];
б)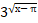 – при х из промежутка [π, +∞);
– при х из промежутка [π, +∞);
в) 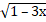 – при х из промежутка (–∞,
– при х из промежутка (–∞,  ].
].
Данные промежутки не пересекаются, следовательно, данное уравнение решений не имеет.
Ответ: решений нет.
1. Решить уравнение: 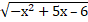 =
= 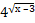 – 1.
– 1.
Окрыленные успехами после первого уравнения, большинство учащихся начинали свое решение с анализа области допустимых значений. Этот поиск привел к тому, что область допустимых значений состоит всего лишь из одного числа 3. Это свидетельствует о том, что если решение существует, то только при х=3. Простая проверка с помощью подстановки х=3 в уравнение позволяет найти окончательный ответ: х=3 – корень уравнения.
Ответ: х=3.
2. Решить уравнение: 2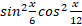 =
= 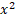 +
+ 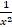 .
.
Аналогичные действия при решении данного уравнения не дают ожидаемого результата, так как область определения – это все числа, кроме 0. Но часть обучающихся не спешит сразу использовать известные методы и после наводящих вопросов приходит к выводу, что можно анализировать не только область определения, но и область значений функций, входящих в уравнение.
Оценивая левую часть уравнения, ученики приходят к выводу, что 2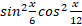 ≤ 2, т.е. левая часть не больше 2. Аналогичный анализ правой части дает неравенство:
≤ 2, т.е. левая часть не больше 2. Аналогичный анализ правой части дает неравенство: 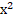 +
+ 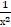 ≥ 2, т.е. правая часть не меньше 2. Единственно возможное решение, когда левая часть равна правой части и равна 2. Решим уравнение:
≥ 2, т.е. правая часть не меньше 2. Единственно возможное решение, когда левая часть равна правой части и равна 2. Решим уравнение: 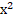 +
+ 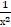 = 2. Корни уравнения: х1 = 1, х2 = –1. Подставив их в левую часть уравнения, убеждаемся, что эти числа не удовлетворяют, т.е. уравнение не имеет решений.
= 2. Корни уравнения: х1 = 1, х2 = –1. Подставив их в левую часть уравнения, убеждаемся, что эти числа не удовлетворяют, т.е. уравнение не имеет решений.
Ответ: нет решений.
Далее ученикам были предложены шесть уравнений:
3. 5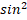 x – 2sinxcosx – 3
x – 2sinxcosx – 3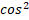 x = 0.
x = 0.
4. 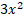 – 2xy –
– 2xy – 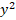 = 0.
= 0.
5. 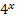 – 7*
– 7*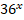 = 18*
= 18*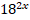 .
.
6. 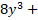 11
11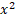 y –
y – 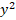 x – 18
x – 18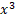 = 0.
= 0.
7. 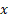 + 6 – 4
+ 6 – 4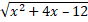 = 8 – 4x.
= 8 – 4x.
8. 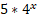 – 2*
– 2*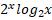 – 3
– 3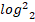 x = 0.
x = 0.
Все уравнения являются однородными, но, к сожалению, никто из школьников этого не заметил. Большинство учеников решили первое уравнение, однако не смогли заметить, что остальные пять уравнений также являются однородными. Безуспешные попытки применить различные методы решения привели школьников к мысли, что снова следует начать с анализа уравнения. Однако анализ области определения и области значений не дал желаемого результата. Но часть школьников, уяснивших основную идею – прежде чем начать решение нестандартного уравнения, проанализируй его – пришли к выводу, что следует изучить сами уравнения и функции, входящие в них.
Наводящие вопросы подвели школьников к поиску сходства между предложенными уравнениями. В ходе обсуждения общего вида однородного тригонометрического уравнения и выделения алгоритма его решения ученики пришли к общему виду однородного уравнения второй степени: A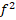 (x) + Bf(x)g(x) + C
(x) + Bf(x)g(x) + C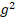 (x) = 0 и способа решения таких уравнений.
(x) = 0 и способа решения таких уравнений.
После такой предварительной работы школьники смогли решить предложенные уравнения.
Рассмотрим решение уравнения: 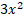 – 2xy –
– 2xy – 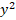 = 0.
= 0.
1) При 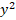 = 0, x = 0, т.е. (0, 0) – решение уравнения.
= 0, x = 0, т.е. (0, 0) – решение уравнения.
2) Пусть теперь 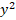 ≠ 0, разделим обе части уравнения на
≠ 0, разделим обе части уравнения на 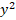 :
:
3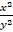 – 2
– 2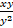 –
– 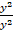 = 0, преобразуем уравнение к виду:
= 0, преобразуем уравнение к виду:
3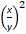 – 2
– 2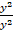 – 1 = 0 и введем замену.
– 1 = 0 и введем замену.
Пусть  = t. Тогда 3
= t. Тогда 3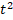 – 2t – 1 = 0.
– 2t – 1 = 0.
 = 1 + 3 = 4, тогда t1 = 1, t2 = –
= 1 + 3 = 4, тогда t1 = 1, t2 = –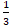 , возвращаясь к замене, получим следующие корни уравнения:
, возвращаясь к замене, получим следующие корни уравнения:  = 1 или
= 1 или  = –
= –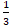 .
.
Ответ: x = y, x = –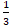 y.
y.
Рассмотрим уравнение: 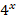 – 7*
– 7*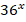 – 18*
– 18*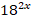 = 0. Преобразуем уравнение к виду:
= 0. Преобразуем уравнение к виду:
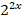 – 7*
– 7*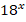 *
*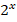 – 18*
– 18*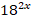 = 0. Разделим обе части уравнения на
= 0. Разделим обе части уравнения на 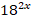 ≠ 0.
≠ 0.
Получим уравнение: 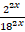 – 7
– 7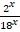 – 18 = 0. Преобразуем уравнение к виду:
– 18 = 0. Преобразуем уравнение к виду:
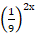 – 7
– 7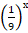 – 18 = 0.
– 18 = 0.
Пусть t =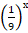 , t> 0. Получим уравнение:
, t> 0. Получим уравнение:  – 7t – 18 = 0.
– 7t – 18 = 0.
По т. Виета найдем корни: t1 = 9, t2 = – 2 – не удовлетворяет.
Вернемся к замене 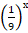 = 9, x = –1.
= 9, x = –1.
Ответ: х = –1.
В ходе обсуждения с учениками аналогично приходим к общему виду однородного уравнения третьей степени: A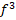 (x) + B
(x) + B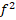 (x)g(x) + Cf(x)
(x)g(x) + Cf(x)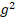 (x) + D
(x) + D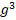 (x) = 0.
(x) = 0.
Решение уравнения 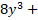 11
11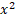 y –
y – 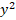 x – 18
x – 18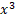 = 0 уже не вызывает особой трудности, так как учениками теперь усвоен способ их решения:
= 0 уже не вызывает особой трудности, так как учениками теперь усвоен способ их решения:
1) Если х = 0, то у = 0, т.е. (0, 0) – решение уравнения.
2) Пусть x ≠ 0, разделим обе части уравнения на 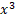
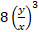 + 11
+ 11 –
– 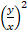 – 18 = 0.
– 18 = 0.
Пусть 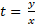 , тогда получим кубическое уравнение:
, тогда получим кубическое уравнение:
8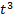 –
– 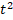 + 11t – 18 = 0.
+ 11t – 18 = 0.
Можно угадать один корень: t=1 и разделить многочлен
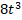 –
– 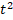 + 11t – 18 на одночлен (t – 1).
+ 11t – 18 на одночлен (t – 1).
Получим квадратное уравнение: 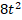 + 7t + 18 = 0.
+ 7t + 18 = 0.
D = 49 – 32*18 < 0 – других решений нет
Таким образом, t = 1, следовательно,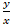 = 1, т.е. y = x.
= 1, т.е. y = x.
Ответ: у = х.
Иногда полезно самим ввести однородность в уравнение.
Рассмотрим уравнение:
10. 4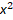 + 12х
+ 12х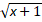 = 27(1 + х).
= 27(1 + х).
Пусть t = 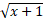 , с помощью данной замены получим однородное уравнение: 4
, с помощью данной замены получим однородное уравнение: 4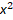 + 12хt – 27
+ 12хt – 27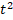 = 0.
= 0.
Так как х = –1 не является корнем уравнения (при этом значении переменная t обращается в нуль), разделим обе части уравнения на 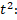
4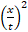 + 12
+ 12 – 27 = 0.
– 27 = 0.
Пусть  = n, получим уравнение 4
= n, получим уравнение 4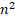 + 12n – 27 = 0.
+ 12n – 27 = 0.
 = 36 + 108 = 144.
= 36 + 108 = 144.
n1 = 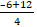 =
=  , n2 =
, n2 = 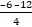 =
=  .
.
Вернемся к замене:  =
=  или
или  = –
= –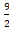 . Отсюда с учетом замены
. Отсюда с учетом замены
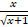 =
=  (1) или
(1) или
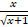 = –
= –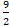 (2).
(2).
Рассмотрим уравнение (1): 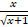 =
=  .
.
Корни данного уравнения:
x1 = 3 – удовлетворяет условию х ≥ 0,
х2 = –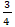 – не удовлетворяет.
– не удовлетворяет.
Аналогично решается уравнение (2): 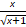 = –
= –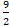 .
.
Корни уравнения:
х1 = 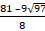 – удовлетворяет условию х < 0,
– удовлетворяет условию х < 0,
х2 = 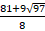 – не удовлетворяет условию.
– не удовлетворяет условию.
Ответ: х1 = 3, х2 = 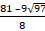 .
.
Рассмотрим функционально-аналитический метод. Часто, анализируя уравнение, можно угадать его корень или корни. Но этого не достаточно для решения уравнения, важным моментом является и доказательство, что других корней нет.
В этом может помочь теорема о корне или ее следствие.
Теорема о корне.
Пусть функция y=f(x) возрастает (или убывает) на множестве Х из D(f), число a – любое из значений, принимаемых f(x) на множестве X, тогда уравнение f(x)=a имеет единственный корень на множестве X.
Следствие из теоремы о корне.
Если функция y=f(x) возрастает, а функция y=g(x) убывает и если уравнение f(x)=g(x) имеет корень, то только один.
Алгоритм решения уравнений функционально-аналитическим методом:
- угадать корень;
- доказать, что других корней нет.
Рассмотрим следующие уравнения:
11. 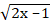 +
+ 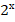 =
= 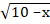 .
.
12. 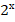 +
+ 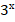 +
+ 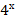 = (3 + х)
= (3 + х)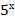 .
.
Решим первое из предложенных уравнений. Можно угадать корень: х = 1. Левая часть уравнения содержит возрастающую функцию (как сумма двух возрастающих функций). Справа находится убывающая функция, поэтому данное уравнение по следствию из теоремы о корне имеет не более одного решения.
Ответ: х = 1.
Решим второе уравнение. Можно угадать корень: х = 0. Докажем, что других корней нет. Рассматривая уравнение в данном виде, ничего нельзя сказать о монотонности функций, входящих в левую и правую части уравнения. Преобразуем уравнение, для этого разделим обе части уравнения на 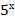 . Получим:
. Получим:
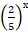 +
+ 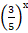 +
+ 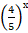 = 3 + х.
= 3 + х.
Слева убывающая функция, справа – возрастающая.
Тогда по теореме о корне других корней, кроме х = 0, нет.
Ответ: х = 0.
Рассмотрим нестандартные замены. Решим следующее уравнение:
13. 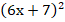 (3х + 4)(х + 1) = 6.
(3х + 4)(х + 1) = 6.
Преобразуем уравнение, стараясь выделить общие части в множителях:
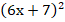 *
* (6х + 8)*
(6х + 8)* (6х + 6) = 6,
(6х + 6) = 6,
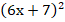 (6х + 8)(6х + 6) = 72.
(6х + 8)(6х + 6) = 72.
Введем замену, пусть 6х + 7 = у, тогда 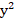 (у + 1)(у – 1) = 72, тогда
(у + 1)(у – 1) = 72, тогда 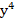 –
– 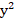 – 72 = 0.
– 72 = 0.
По теореме Виета найдем корни уравнения:
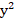 = – 8 – решений нет,
= – 8 – решений нет,
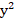 = 9, т.е. у = ± 3.
= 9, т.е. у = ± 3.
Вернемся к замене:
6х + 7 = 3 или 6х + 7 = – 3. Найдем корни уравнения:
х = –  или х = –
или х = – 
Ответ: х = – , х = –
, х = –  .
.
Выводы. Резюмируя все вышесказанное, можно сделать вывод. Решая нестандартные уравнения, не следует торопиться, и прежде чем приступить к его решению, полезно сделать подробный анализ самого уравнения: проанализировать вид уравнения, попытаться отнести его к известному типу уравнений; выделить функции, входящие в уравнение; проанализировать область определения (ОДЗ); оценить область значений левой и правой частей уравнения. И только после этого приступать к решению самого уравнения. Ведь довольно часто уже этих мер бывает достаточно, чтобы решить довольно сложные на первый взгляд уравнения.



