Исходя из того, что работоспособность любой механической системы определяется во многом надежностью, то, по-видимому, целесообразно рассмотреть процесс накопления повреждений в главной балке металлургического мостового крана под воздействием случайного режима циклических напряжений, обусловленных важнейшим воздействием сил [2, 8-10].
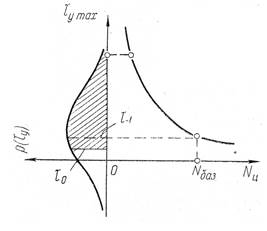
Рис.1. Распределение напряжений и закономерность усталостного накопления повреждения в элементах системы
Принимая внешнее воздействие (нагрузку) в виде узкополосного стационарного гауссовского процесса, определим меру повреждений [1, 2]:
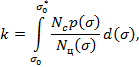(1)
где 
– суммарное число циклов до разрушения конструкции; 
– плотность распределения амплитуд напряжений, превышающих заданный (допускаемый) уровень; 
– функция, связывающая длительно действующие напряжения с числом циклов до разрушения (накопление повреждений в конструкции) и подчиняющаяся степенной зависимости 
– напряжение, приближенно соответствующее пределу усталости материала элемента конструкции; 
– допускаемый уровень напряжений.
Накопление повреждений конструкции или ее долговечность определим
(2)
где 
– число циклов действующих напряжений в единицу времени (например, в течение суток работы системы).
Подставив в эту формулу выражение для из уравнения (1), в окончательном виде будем иметь
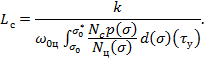(3)
Если принять [2] распределение максимумов процесса нагружения, приближенно следующего закону Релея, и ввести выражение для :
тогда с учетом выражения для функции; получим [2, 8]:
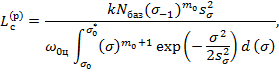(5)
где 
– среднеквадратическое отклонение напряжений, действующих на конструкцию;
; 
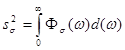– энергетический спектр напряжений материала элемента конструкции, определяемый из известной спектральной плотности нагрузок на "входе" системы и ее передаточной функции.
Приведем интеграл в формуле (5) к виду [8], выполним подстановку:
,
и изменив предел интегрирования, представим его как разность:
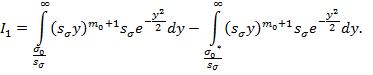(6)
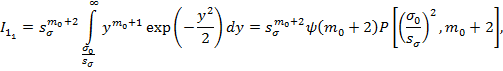(7)
где 
.
Также определим второй интеграл в формуле (6):
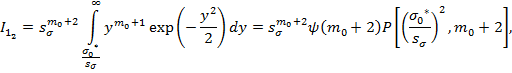(8)
Получим расчетную зависимость долговечности конструкции при установившемся режиме нагружения [2-10]:
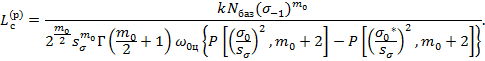(9)
Расчетная зависимость (9) учитывает распределение максимальных значений напряжений и содержит параметры случайного процесса. Кроме того, в ее состав входят параметры кривой усталости, описывающей закономерность накопления повреждений в конструкции и потерю ее работоспособности при установившемся процессе нагружения.
Аналогично выполняются все выкладки по определению долговечности системы, если рассматривать распределение амплитуд нагрузок, превышающих заданный уровень, следующих закону Пирсона.
Долговечность системы можно определить, если рассматривать распределение максимальных (экстремальных) значений напряжения в элементе конструкции при действии на нее случайного процесса нагружения:
(10)
Распределение экстремальных значений позволяет выявить наличие максимума интенсивности напряжений в конструкции в течение рассматриваемого временного интервала, который будет иметь место с определенной вероятностью только один раз. Этот временной интервал, исходя из формулы (3), будет:
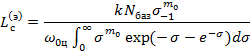(11)
Интеграл знаменателя (11) приводится к модифицированной функции Бесселя.
Расчет долговечности системы, исходя из анализа случайного процесса нагружения, предполагает проведение экспериментальных работ для определения параметров зависимости потери работоспособности несущей конструкции мостового металлургического крана или выбор их ориентировочных значений по имеющимся данным.
Рецензенты:
Черчинцев В.Д., д.т.н., профессор, заведующий кафедрой промышленной экологии и безопасности жизнедеятельности ФГБОУ ВПО Магнитогорский государственный технический университет им. Г.И. Носова; г. Магнитогорск;
Бигеев В.А., д.т.н., профессор, директор института машиностроения, металлургии и металлообработки ФГБОУ ВПО Магнитогорский государственный технический университет им. Г.И. Носова; г. Магнитогорск.