Для случайных величин формируются свои алфавиты:
![]() ,
где k –
номер стадии обработки, mk
– фактор k-й стадии
обработки,
,
где k –
номер стадии обработки, mk
– фактор k-й стадии
обработки, ![]() — полуинтервалы, образующие алфавит каждого
фактора. Варианты сочетаний алфавитов исследуемых технологических величин
— полуинтервалы, образующие алфавит каждого
фактора. Варианты сочетаний алфавитов исследуемых технологических величин ![]() :
: ![]() .
.
Аналогично для составляющих алфавитов
входных величин ![]() (где
(где ![]() ,
,
![]() — значность алфавита l-го входа на k-ом агрегате,
— значность алфавита l-го входа на k-ом агрегате, ![]() — номер входа (элементов сырья,
полуфабрикатов) на k-ом
агрегате) формируются варианты сочетаний алфавитов входов
— номер входа (элементов сырья,
полуфабрикатов) на k-ом
агрегате) формируются варианты сочетаний алфавитов входов ![]() :
:
![]() .
.
Варианты сочетаний алфавитов выходов ![]()
(![]() —
составляющая алфавитов r-го выхода после k-й стадии
обработки,
—
составляющая алфавитов r-го выхода после k-й стадии
обработки, ![]() — знатность алфавита r-го выхода,
— знатность алфавита r-го выхода, ![]() — номер выхода).
— номер выхода).
Для каждого режима обработки (сочетания алфавитов состояний) необходимо определить частоты реализации различных сочетаний алфавитов выходных свойств.
Таким образом, можно выделить сочетания алфавитов входов ![]() и технологических параметров
и технологических параметров ![]() ,
которые позволяют получать оптимальное сочетание выходных алфавитов
,
которые позволяют получать оптимальное сочетание выходных алфавитов ![]() .
.
Каждое сочетание ![]() является вариантом
реализации технологии
является вариантом
реализации технологии ![]() . Обозначим оптимальный элемент алфавита выходных свойств
. Обозначим оптимальный элемент алфавита выходных свойств ![]() .
.
Для анализа выбрано R показателей качества. В каждом
конкретном опыте число этих показателей, соответствующих среднему элементу
алфавита ![]() (совместная частота nR), неодинаково. Частота nR
изменяется в пределах 0£nR£R
и показывает, сколько
выходных параметров соответствует требованиям стандартов. Обозначим
(совместная частота nR), неодинаково. Частота nR
изменяется в пределах 0£nR£R
и показывает, сколько
выходных параметров соответствует требованиям стандартов. Обозначим ![]() — число опытов, равное
— число опытов, равное ![]() , т.е. те опыты, которые при реализации
технологии
, т.е. те опыты, которые при реализации
технологии ![]() попадают в подмножество
попадают в подмножество ![]() . Опыты, реализованные по технологии
. Опыты, реализованные по технологии ![]() , но не попадающие в подмножество
, но не попадающие в подмножество ![]() , будем объединять в
, будем объединять в ![]() . Причем
. Причем ![]() —
число опытов, соответствующих
—
число опытов, соответствующих ![]() ,
, ![]() —
— ![]() и
т.д. nR=0 при
условии, если все показатели не соответствуют требованиям стандарта. nR=R,
если для каждого показателя эти требования выполняются. На практике часто nR¹R,
так как одна или несколько выходных характеристик выходят за рамки требований.
Для каждого сочетания
и
т.д. nR=0 при
условии, если все показатели не соответствуют требованиям стандарта. nR=R,
если для каждого показателя эти требования выполняются. На практике часто nR¹R,
так как одна или несколько выходных характеристик выходят за рамки требований.
Для каждого сочетания ![]()
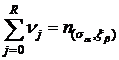
Информация для всех ненулевых сочетаний алфавитов технологических факторов заносится в таблицу 1.
Таблица 1
Частоты получения алфавитов выходов для исследуемых
технологических подмножеств
|
Технологическое подмножество
|
Cочетания алфавитов на всех агрегатах
|
Частота падания в
|
Выходные параметры |
Совместная частота nR |
||||||||||||
|
y1 |
… |
yR |
||||||||||||||
|
Частота получения алфавитов выходов |
||||||||||||||||
|
0 |
1 |
… |
R |
|||||||||||||
|
|
… |
|
… |
|
… |
|
||||||||||
|
n0 |
n1 |
… |
nR |
|||||||||||||
|
|
11…11 |
n1 |
|
|
|
|
|
|
||||||||
|
|
11…12 |
… |
|
|
|
|
|
|
||||||||
|
…. |
…. |
… |
|
|
|
|
|
|
||||||||
|
|
kk…kk |
nD |
|
|
|
|
|
|
||||||||
|
|
||||||||||||||||
Технологическая цепочка ![]() ,
имеющая максимальное значение критерия оценки эффективности оптимальных режимов
функционирования сложных систем [6-10], может быть выбрана в качестве
оптимальной технологии.
,
имеющая максимальное значение критерия оценки эффективности оптимальных режимов
функционирования сложных систем [6-10], может быть выбрана в качестве
оптимальной технологии.
На следующем этапе можно оценить вероятности переходов в
состояние ![]() на k-м агрегате при условии, что на (k-1)-м агрегате реализовалось
состояние
на k-м агрегате при условии, что на (k-1)-м агрегате реализовалось
состояние ![]() и сформировать переходные матрицы (табл.
2), в которых строки матрицы занумерованы предыдущими состояниями, а столбцы –
последующими. Пример реализации для двух случайных величин на каждом агрегате и
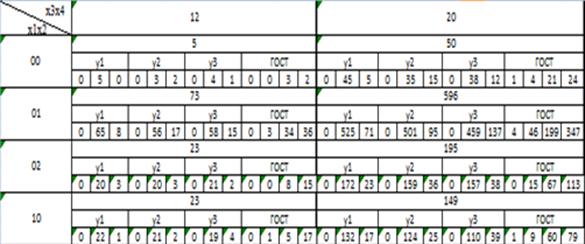
трех выходных величин (фрагмент переходной матрицы) приведен в таблице 3.
Например, переход из состояния 00 для х1х2 в состояние 12 для х3х4 осуществлен
5 раз, по у1 в средний (оптимальный) элемент алфавита попали все 5 опытов, по
у2 – 3 опыта, по у3 – 4 опыта. В итоге совместные частоты для данного перехода:
n0=0,
n1=0,
n2=3,
n3=2.
и сформировать переходные матрицы (табл.
2), в которых строки матрицы занумерованы предыдущими состояниями, а столбцы –
последующими. Пример реализации для двух случайных величин на каждом агрегате и
трех выходных величин (фрагмент переходной матрицы) приведен в таблице 3.
Например, переход из состояния 00 для х1х2 в состояние 12 для х3х4 осуществлен
5 раз, по у1 в средний (оптимальный) элемент алфавита попали все 5 опытов, по
у2 – 3 опыта, по у3 – 4 опыта. В итоге совместные частоты для данного перехода:
n0=0,
n1=0,
n2=3,
n3=2.
Таблица 2
Переходная матрица из агрегата k-1 в агрегат k.
|
Х1 |
ξ1(k) ……………..……….. ξβ(k) ……………..……….. ξB(k) |
|
|||||||||||
|
ξ'1(k-1) . ξ'β(k-1) .
ξ'B(k-1) |
Выходные параметры |
Совместная частота nR |
|||||||||||
|
y1 |
… |
yR |
|||||||||||
|
Частота получения алфавитов выходов |
|||||||||||||
|
0 |
1 |
… |
R |
||||||||||
|
|
… |
|
… |
|
… |
|
|||||||
|
n0 |
n1 |
… |
nR |
||||||||||
|
|
|||||||||||||
Таблица 3
Фрагмент реализации переходной матрицы для двух случайных величин.
Заключение
Выбранная стратегия поиска оптимальных технологических режимов в дискретных клеточно-иерархических системах позволяет формировать оптимальные технологические траектории, обеспечивающие получение требуемых свойств с максимальной частотой.
Рецензенты:Володин И.М., д.т.н., профессор, проректор по научной работе, ФГБОУ ВПО «Липецкий государственный технический университет», г. Липецк;
Шмырин А.М., д.т.н., доцент, заведующий кафедрой высшей математики, ФГБОУ ВПО «Липецкий государственный технический университет», г. Липецк.




 X
X