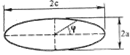Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Длительная эксплуатация стальных стационарных платформ для добычи нефти и газа, установленных на морских месторождениях,  требует оценки их долговечности, что приводит к необходимости введения некоторого усталостного критерия. В качестве такого критерия может выступать усталостная трещина. Как показали экспериментальные исследования разных авторов, при возникновении усталостной трещины глубиной 2–3 мм  прочность образцов, моделирующих крупногабаритные объекты, резко падала, и их разрушение происходило при напряжениях, значительно меньше номинальных [1, 2, 12]. Во всех опытах усталостные трещины вызывали разрушение при низких номинальных напряжениях сразу после того, как их глубина превышала 2–3 мм. Эти опасные дефекты, образующиеся как в основных конструктивных элементах, так и в сварных соединениях,  представляют собой серьезную опасность и могут при определенных условиях привести к их разрушению [1-12]. Кроме того, усталостные трещины могут нарушить герметичность конструкции МСП и вызвать течь с последующим затоплением. Устранение образующихся трещин сопряжено с внеплановыми простоями, что сказывается на экономической рентабельности сооружений. Важность учета требований обеспечения усталостной долговечности признана всеми ведущими организациями в мире, занимающимися освоением морских нефтегазовых месторождений. Определимся с понятиями «усталость» и «усталостная трещина». Усталость металла – процесс постепенного накопления повреждений в материале под действием переменных напряжений, вызванных различными нагрузками и воздействиями [2, 3, 7-12] (температурными, коррозионными, вибрационными и др.), приводящими к изменению свойств металла и образованию трещин. Трещина, постепенно развиваясь и ослабляя сечение, вызывает внезапное разрушение как конструктивных элементов МСП, так и сварных соединений. Причем в процессе испытания модельных образцов опорного блока, которые выполнялись автором, в основном трещины зарождались в сварных соединениях, однако был отмечен случай, когда трещина при испытаниях зародилась в основном металле и вызвала разрушение испытуемого образца до появления трещин в сварных соединениях. Также следует отметить наличие зарождающихся трещин в зоне прикрепления экспериментального образца к грунту. Автор объясняет это явление большими значениями изгибающих моментов, возникающих в сечении испытуемого образца, закрепленного по консольной схеме. Широко известно, что основным механизмом, вызывающим развитие усталостных трещин, является действие переменных нагрузок и воздействий, которые в свою очередь вызывают изменяющиеся с определенной частотой переменные напряжения. Ранее автором были систематизированы понятия «нагрузка» и «воздействия» [1,7-11] и описано их влияние на возникновение и развитие усталостных трещин. Предложены математические методы, позволяющие описать эти воздействия и установить их влияние на напряженное состояние исследуемых элементов. В настоящей статье предлагается решение важного практического вопроса, а именно описание процесса возникновения, развития и раскрытия трещин для основных конструктивных элементов и сварных соединений опрного блока морской стационарной платформы (ОБ МСП). Задача  настоящей статьи состоит в анализе существующих методов, описывающих кинетику распространения трещин, и в разработке на этой основе методики, описывающей эти процессы в сварных соединениях и основных конструктивных элементах ОБ МСП. Кратко опишем  основные понятия, относящиеся к процессу трещинообразования. Ключевым понятием является так называемая упругая энергия, под которой понимается энергия внешних сил, затраченная на упругую  деформацию элемента. Это вся работа, проделанная в течение упругой деформации, сохраняется как некоторая энергия, которая затем восстанавливает элемент после снятия напряжения [2, 12]. Однако при наличии в элементе трещины величина упругой энергии изменяется. Если упругая энергия деформация пластинки без трещины при заданном уровне напряжения равна U0, то при наличии трещины она будет определяться исходя из выражения:

, (1)

где E – модуль упругости материала. Выражение    показывает уменьшение упругой энергии деформации пластинки вследствие наличия в ней трещины, 2а — полная длина трещины. Это выражение получено в предположении, что при наличии в  пластине трещины размером 2a упругая энергия деформации отсутствует в объеме материала, равном  . Величина  – поверхностная энергия трещины, учитывающая образование двух поверхностей; T – удельная поверхностная энергия, равная работе, необходимой для образования единицы новой поверхности. Первоначально полная энергия тела растет с увеличением длины трещины, что свидетельствует о том, что рост трещины может происходить только при увеличении напряжений. В этом случае происходит стабильный рост трещины. При увеличении размеров трещины до некоторого критического размера трещины растут за счет запаса упругой энергии без дополнительного увеличения напряжений. Такое развитие трещин называют нестабильным. Оно характерно для хрупкого разрушения. Процессы развития трещин описываются при помощи коэффициентов интенсивности напряжений К, которые определяют изменение напряженно-деформированного состояния в вершине трещины. Значения К с учетом вида приложенной нагрузки, при которых начинается нестабильное разрушение трещин в условиях плоской деформации, называются критическими значениями коэффициента интенсивности напряжений , , . 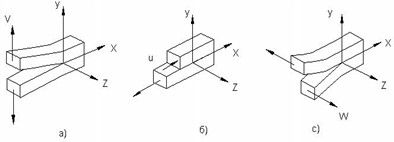В зависимости от вида приложенной нагрузки деформирование тела с трещиной может происходить по одной из следующих основных схем [12]: I  (растяжение, рис. 1а) — поверхности трещины расходятся друг от друга;  II (поперечный сдвиг, рис. 1б) — поверхности трещины скользят одна по другой в поперечном направлении; III (продольный сдвиг, рис. 1с) — поверхности трещины скользят одна по другой в продольном направлении.

 

Рис. 1. Классификация трещин в зависимости от вида приложенной нагрузки	Рис. 2. Схема трещины эллиптической формы

 

         Значения коэффициентов интенсивности напряжений К сильно зависят от вида трещины. По мнению автора, большинство трещин как в сварных соединениях, так и в основных КЭ можно описать при помощи трещины эллиптической формы (рис. 2). Это можно объяснить опытом наблюдения за развитием трещин, так как наиболее часто трещины зарождаются в углах или на краях тел, где имеется концентрация напряжений. Такие трещины распространяются внутрь тела и имеют форму эллипса или четверти эллипса. Напряженное состояние в таких трещинах с учетом кривизны поверхности трещины определено Снеденном и другими авторами в работах [2]. Для эллиптической трещины коэффициент интенсивности напряжений определяется по формуле:

             (2)

А Ф с точностью до 5% процентов можно определить по формуле:

                                          (3)

Наибольшие значения коэффициент интенсивности напряжений принимает при значениях ϕ=900. В этом случае формулу можно привести к виду [2]:

                ,               (4)

,                     (5)

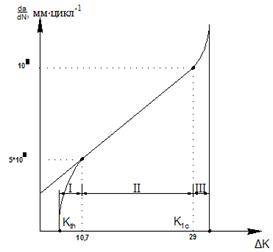
       Зная значения коэффициентов интенсивности напряжений, можно определить скорость роста трещины, которая является некоторой функцией от них и описывается при помощи кинетической диаграммы роста усталостной трещины, схема которой приведена на рисунке. Следует отметить, что этот рост неравномерен, условно его можно описать тремя участками с различными скоростями роста [12]: 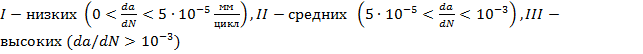 Границами перехода от одного участка к другому являются пороговое  и критическое  значение коэффициентов интенсивности напряжений, а скорость роста рассчитывается по формуле:

                                         (6)

где: а — приращение длины трещины за один цикл,  — размах коэффициентов интенсивности напряжений, n и С — некоторые константы материала. Пороговый коэффициент интенсивности напряжений для стальных конструкций, в том числе и для опорных блоков МСП, можно рассчитать в соответствии с данными работы по формуле Г.В. Матохина [4]:

                                     (7)

где   — пороговый коэффициент интенсивности напряжений, МПа∙м0,5;  – временное сопротивление стали, МПа. Исходя из того, что временное сопротивление описанного в 3 главе сварного соединения составляет 490 МПа, значение порогового коэффициента интенсивности напряжений будет равно 10,7 МПа∙м0,5. Для описания кинетики развития трещины на участке I автором предлагается использовать формулу, полученную опытным путем в работе [5]:

             (8)

где: а — приращение длины трещины за один цикл,  – размах коэффициентов интенсивности напряжений,  определяется по формуле:

                             (9)

       где: R1 — пороговый коэффициент асимметрии цикла, принимаемый в соответствии с данными работы [5]. После определения параметров прямой, описывающей скорость роста на участке I, и расчета порогового коэффициента интенсивности напряжений необходимо определить параметры прямой на участке II. Для этого автором предлагается использовать уравнение, полученное в работе [5]:

   (10)

где: а — приращение длины трещины за один цикл,  — размах коэффициентов интенсивности напряжений, -определяется по формуле:

                       (11)

    где значение R1 то же, что и в формуле (9).

Предложенное уравнение действует до достижения   критического значения коэффициента интенсивности  напряжения  , который характеризует начало нестабильного  развития трещин, который можно определить   прямыми эксперимен­тальными методами по ГОСТ 25.506-85 либо исполь­зовали для расчета этой величины зависимость, предложенную в работе [3]:

                      (12)

где E – модуль упругости; v – коэффициент Пуассона;  – ударная вязкость на образцах типа Шарпи; k – без­размерный коэффициент пропорциональности, рассчиты­ваемый по формуле:

                 (13)

где σв и σт  — временное сопротивление и предел текучести стали. Ударную вязкость исследуемых материалов можно определять из данных сертификатов, по нормативным документам; в некоторых случаях можно использовать данные, приведенные в РД РТМ 26-298-78 (табл. 1).

Таблица 1

Ударная вязкость сталей сварного соединения при различных комбинациях свариваемых сталей

Свариваемые стали	Ударная вязкость при +20 0С кГм/см2	Ударная вязкость при –400С кГм/см2
Углеродистая + низколегированная или хромомолибденовая сталь	5	2,5
Углеродистая + аустенитная сталь	5	2,5
Низколегированная или хромомолибденовая + аустенитная сталь	5	2,5

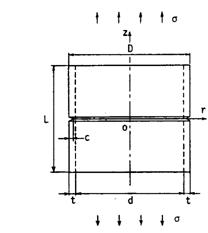
            В результате расчетов установлено, что для исследуемого нами сварного соединения пороговый коэффициент интенсивности напряжений составляет 29 МПа∙м0,5. Те же принципы построения кинетической диаграммы усталости применимы для основных конструктивных элементов опорного блока МСП. На основе проведенных расчетов автором была построена кинетическая диаграмма усталостного разрушения сварных соединений и основных конструктивных элементов опорных блоков морских стационарных платформ (рис. 3). Так, например, для раскоса опорного блока, представляющего собой полую трубу, при наличии поверхностной кольцевой трещины (рис. 4) как при изгибе, так и при растяжении величины коэффициентов интенсивности напряжений можно определить по формуле:

                 (14)

где: σ — величина напряжения при растяжении или изгибе, с — глубина трещины, отсчитываемая с поверхности, а F — функция, определяемая по формуле:

    (15)

где: λ — отношение глубины трещины с к толщине стенки конструктивного элемента t, а соответствующие коэффициенты определяются из таблицы 2.

Таблица 2

Коэффициенты уравнения (15)

 

Рис. 3. Кинетическая диаграмма усталостного разрушения сварных соединений и основных конструктивных элементов опорных блоков морских стационарных платформ	Рис. 4. Схема конструктивного элемента МСП при наличии кольцевой трещины

 

           В диссертации И.В. Староконя был проведен анализ напряженного состояния элементов опорного блока и дано понятие эквивалентных напряжений, т.е. таких напряжений, при которых сложное напряженное состояние элементов можно заменить одноосным растяжением образца, что упрощает применение формул (14) и (15). Для  других видов трещин формулы расчета коэффициентов интенсивности напряжений приведены в работе [6].

Рецензенты:

Бородавкин П.П., д.т.н., профессор, генеральный директор АО «Интергаз», 
г. Москва;

Литвин И.Е., д.т.н., генеральный директор ООО «СТД», г. Москва.