К подобным системам относятся самонастраивающиеся системы с эталонными моделями (СНС с ЭМ). Исследование СМС с ЭМ показало их большие возможности, однако широкоевнедрение сдерживается трудностью выбора эталонной модели, высокой чувствительностьюнастройки параметров к характеристикам входных сигналов, взаимовлиянием контуров настройки.
С целью преодоления недостатковработы САУ в алгоритм настройки САУ (и в его структуру) в дополнение к эталонной модели вводится вторая эталонная модель,называемаяподстраиваемой моделью (ПМ) [2].С помощью ПМ осуществляется параметрическая идентификация САУ, при которой ПМ подстраивается к настраиваемой САУ. После чего выполняется настройка ПМ к заданным требованиям качества работы САУ с использованиемэталонной модели (ЭМ) специального вида (параметрическое множество ЭМ).
Дуальный характер рассматриваемой схемы настройки САУ,наряду с использованием алгебраических методов анализа САУ, дает возможность с помощью алгоритма самонастройки решить задачу идентификации[6]. Поэтому в статье основное внимание уделяется алгоритму настройки, поскольку аналогичные вычислительные процедуры могут быть использованы и на этапе идентификации динамики объекта.
1. Алгоритм синтеза самонастраивающейся системы автоматического управления с двумя эталонными моделями
Для нахождения области допустимых настроек используются методы нелинейного программирования [1]. Причем в качестве искомых значений коэффициентов данной зоны выбирается точка, в которую вырождается область допустимых настроек при пропорциональном увеличении требований к переходным процессам (например, уменьшение максимально допустимого перерегулирования, уменьшение времени вхождения в трубку точности и т.д.).
Математическое описание ПМ формируется в виде совокупности дробно-рациональных (полиномиальных) выражений от настраиваемыхпараметров, определяющих реакцию САУ на соответствующий тестовый сигнал [3, 4].
Приведенная на рис.1 схема функционирования поясняет взаимодействие частей программы, реализующей алгоритм автомата-настройщика (АН) в его классическом понимании. В соответствии со схемой порядок работы алгоритма следующий.
Тестовый сигнал
поступает на вход настраиваемой системы и подстраиваемой модели.
Параметры ПМ 
и
, равны номинальным значениям соответствующих параметров в
реальной настраиваемой системе. После прохождения тестового сигнала ошибка
рассогласования поступает в блок идентификации.
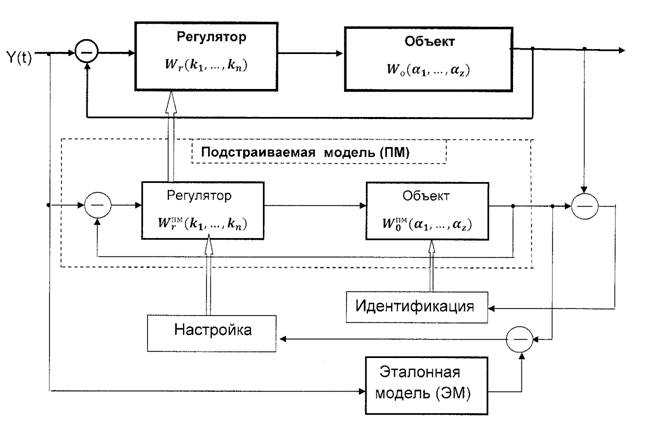
Рис. 1. Функциональная схема автомата-настройщика (АН)
В соответствии с
алгоритмом идентификации в ПМ вычисляются значения параметров ,которые являются
соответствующими оценками данных параметров в реальной системе [5].
В случае, если настраиваемая САУ линейна, достаточно рассмотреть лишь один тестовый сигнал на этапе идентификации, например, ступенчатый, как наиболееширокополосный и вынуждающий систему проявить все динамические особенности.Таким образом, ПМ подстраивается к реальной системе, и в дальнейшем происходит настройка подстраиваемой модели, а реальная система отключается от процесса настройки [8].
После этапа идентификации тестовый сигнал подается на вход подстраиваемой модели и эталонной модели. ЭМ задает множество желаемых переходных процессов, удовлетворяющих требованиям к качеству регулирования. Ошибка рассогласования поступает в блок настройки, в котором минимизируется выражение:
Предположим далее,
что при полученных значениях настраиваемых параметров (k1,...,kn) (обозначим значения настраиваемых параметров в виде вектора
), не удовлетворяются первичные показатели качества, то есть
перерегулирование Ϭ>Ϭд, Т>Тппд. Следовательно,необходимо найти такой вектор К, при котором
требования,предъявляемые к первичным показателям качества удовлетворяются.
2. Пример реализации алгоритма настройки
Построение алгоритма
настройки рассмотрим на примере следящей системы (СС) с учетомследующих показателей
качества:перерегулирование Ϭ, время переходного
процесса 
и статическая точность 
.В качестве передаточной функции ЭМ рассмотрим колебательное
звено, которое,как известно,хорошо аппроксимируетреакциюСС на единичное
ступенчатое воздействие 1(t).
Пусть постоянная
времени Т и коэффициент демпфирования ξ передаточной функции ЭМ такие, что 
(t) удовлетворяет предъявленным требованиям к качеству
регулирования.Далее представим (t) в видеразложения в ряд по полиномам Чебышева:
Тогда
а решение системы нелинейных алгебраических уравнений вида:
удовлетворяет предъявляемым требованиям, то задача считается решенной.
Следует отметить, что
успех решения задачи в значительной степени зависит от удачного выбора кривой(t), то есть параметров эталонного колебательного звена. Поэтому
имеет смысл,исходя из заданных требований к качеству регулирования, определить область
, такую, что переходная функция колебательного звена со
значениями ξ и Т из этой области, удовлетворяет
требуемому качеству. Пусть имеется разложение переходной функции колебательного
звена в виде явной зависимости коэффициентов разложения от ξ и T, то есть
Тогда получим функцию
) в виде 
и будем ееминимизировать по переменным ,ξ,Т:
Таким образом, из всего множества допустимых реакций выбирается та, которая наиболее адекватна динамике рассматриваемой системы.Для решения задачи необходимо выбрать N и определить области допустимых значений для заданных требований к качеству управления.
В результате получены
ограничения на β и 
, при которых переходный процесс 
(t) удовлетворяет предъявляемым требованиям к качеству
управления с точки зрения заданных показателей качества,значит для
рассматриваемого примера определена 
Выводы
Разработанный алгоритм адаптации САУ обеспечивает накопление информации о динамике управляемого объекта и построение многовариантного прогноза состояния системы в пространстве настраиваемых параметров. Таким образом, в контур САУ фактически вводится акцептор действия, прогнозирующий в реальном масштабе времени наилучший вариант настройки САУ в рамках заданных критериев качества.
Рецензенты:Пролетарский А.В., д.т.н., профессор, декан факультета «Информатика и системы управления», зав. кафедрой «Компьютерные системы и сети», МГТУ им. Н.Э.Баумана, г. Москва;
Неусыпин К.А., д.т.н., профессор, профессор кафедры «Системы автоматического управления», МГТУ им. Н.Э.Баумана», г. Москва.