. Полуширина резонансного
пика такой решетки может достигать 0,005 нм [9], что свидетельствует о
возможном увеличении разрешающей способности измерений в 10–50 раз по сравнению
с датчиком на ВБР.
Как показано на рисунке 1, ВБР с фазовым p-сдвигом характеризуется неоднородностью с размером p, расположенным в определенном месте ее структуры по длине (показано для середины решетки).
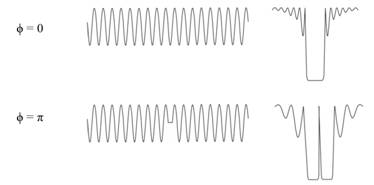
Рис. 1. Модуляция коэффициента преломления и спектральная характеристика ВБР
(без фазового сдвига f=0 и с фазовым сдвигом f=π)
Для математического моделирования спектральных характеристик ВБР применяются различные методы, включая метод матриц передачи, метод матриц Джонса, метод связанных мод. Получение наиболее точных спектральных характеристик ВБР с фазовым сдвигом при их равномерном растяжении/сжатии возможно при использовании метода связанных мод [10]. Наибольшее приближение к реальным характеристикам ВБР, подверженных изгибному натяжению, получают с помощью метода матриц передачи для отрезков до и после изгиба и с учетом линейного изменения этих отрезков по градиенту изгиба [9].
Моделирование спектральных характеристик ВБР с фазовым p-сдвигом при равномерном растяжении/сжатии. Модуляция коэффициента преломления равномерной ВБР представляет собой синусоидальный процесс с постоянной амплитудой, который может быть записан следующим образом:
n(z) = 
,
(1)
а
для 
=p
примет вид:
n(z)=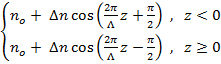 
.
(2)
Рассмотрим
две встречные волны 
и
,
распространяющиеся в волокне через ВБР 
с
длиной волны l, где 
зависит
от участка распространения волны (до или после фазового сдвига с координатой 
)
. (3)
как показано на рисунке 2.
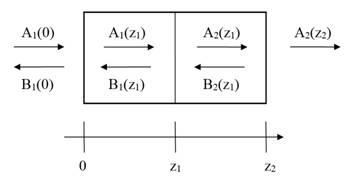
Рис. 2. Распространение встречных волн в ВБР с фазовым сдвигом
Распространение таких волн может быть описано связанными дифференциальными уравнениями, в которых для дальнейшего анализа необходимо вставить значение фазового сдвига:
, (4)
(5)
где
коэффициент связи 
(h
- коэффициент локализации мод); 
–
параметр расстройки, который представляет собой разность между постоянными
распространения 
и
волновым числом решетки 
Данные уравнения могут быть представлены общим уравнением вида:
(6)
которое имеет решения для обеих половин решетки.
Введем граничные условия:
,
и получим:
(7)
, (8)
где
.
Определим параметры окна прозрачности ВБР с фазовым сдвигом
T(z)=
. (9)
С использованием предыдущего выражения получим:
T(z)=
.
(10)
После определения C и D из граничных условий получим для окна прозрачности:
T(
(11)
где
E=
F=
Для
получим:
T(
(12)
На рисунке 3 показана зависимость полученной ширины окна прозрачности на полувысоте от коэффициента модуляции. Из анализа рисунка 3 видно, что возможно получение как сверхузких окон прозрачности, так и достаточно широких, способных регистрировать изменения температуры в пределах 5–10°С при чувствительности решеток от 1 до 10 пм на 1°С, что вполне достаточно для построения систем автоматического регулирования.
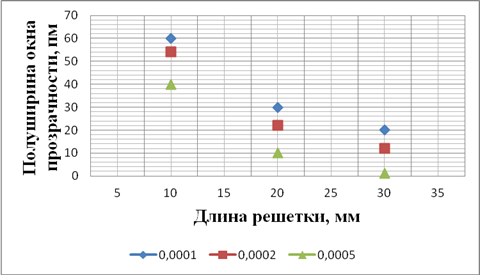
Рис. 3. Зависимость ширины окна прозрачности решетки на полувысоте
от ее длины и глубины коэффициента модуляции
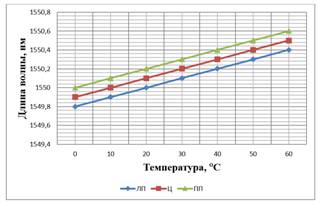
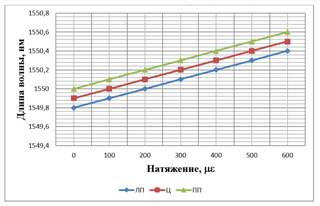
При равномерном растяжении/сжатии ВБР с фазовым p-сдвигом соответствуют по характеристическому отклику классическим ВБР [10]. На рисунке 4,а показан рассчитанный отклик ВБР с фазовым p-сдвигом на изменение температуры, на рисунке 4,б – натяжения. Полученные значения трендов показали, что чувствительность измерений ВБР с фазовым p-сдвигом от температуры составила ~10 пм/°С, а от натяжения ~1 пм/me по центру окна прозрачности решетки. Полученные данные были использованы в системных разработках сенсорных систем различного назначения [2, 4-5].
а б
Рис. 4. Зависимость сдвига центральной длины волны окна прозрачности
ВБР с фазовым p-сдвигом от температуры (а) и натяжения (б):
ЛП – левый пик, Ц – центр, ПП – правый пик решетки (см. рис. 1)
Моделирование спектральных характеристик ВБР с фазовым p-сдвигом при изгибном натяжении. ВБР с фазовым p-сдвигом в случае приложенных к ней изгибных сил могут быть численно описаны комплексным методом, основанным на методах связанных мод и матриц передачи, которые известны как точные и эффективные методы численного моделирования.
Характеристики ВБР
описываются произведением матриц 2´2 каждого однородного
элемента решетки, что позволяет в итоге получить полную матрицу передачи ВБР.
ВБР разбивается на N однородных секций, для которых определяются коэффициенты
отражения 
и пропускания 
как амплитуды
распространяющихся вперед и назад мод после прохождения i-ой секции:
= Fi 
(13)
где матрица передачи каждой секции описывается следующим образом
Fi =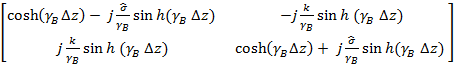 
, (14)
где 
- длина i-ой секции; 
- квадратный корень из -1; 
- общий «постоянный»
коэффициент связи мод; 
– общий «переменный»
коэффициент связи мод для секции
.
(15)
После определения матриц для каждой секции можно записать:
= F 
(16)
.
(17)
Для обеспечения фазового p-сдвига введем матрицу 
между
матрицами 
и 
в (17), которая определяется
как:
,
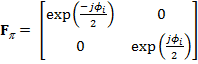(18)
где 
Начальные условия для матрицы передачи определим как:
= 
(19)
а коэффициенты отражения и пропускания как:
= 
,
(20)
= 
.
(21)
Проведенные по методике [9] исследования показали, что провал в ВБР, вызванный фазовым сдвигом, уширяется с сохранением градиента крутизны общего уширения ВБР.
На рисунке 5 показана спектральная характеристика ВБР до (А) и при (Б) воздействии. При отсутствии воздействия ширина провала составляла 0,01 нм, при κ=5 м-1 ~ 0,16 нм. Использовался пакет прикладных программ Optigrating 4.2.
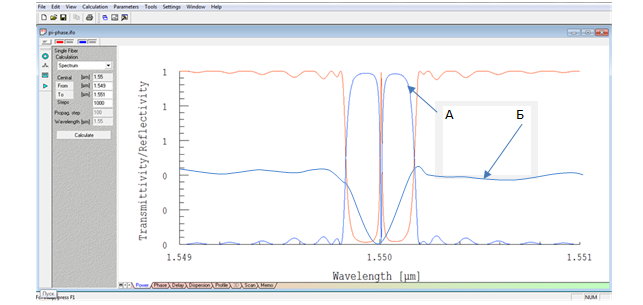
Рис. 5. Спектральная структура ВБР с фазовым p-сдвигом
и ширина окна прозрачности до (А) и при (Б) воздействии
Таким образом, если для измерения ширины решетки необходимо использовать сложное спектральное оборудование, то для измерения ширины провала может быть использована методика маломодового двух- или четырехчастотного зондирования без перестройки частоты лазера с двумя неравными разностными частотами. Процедура определения резонансной длины волны ВБР, ее высоты и ширины окна прозрачности на полувысоте, предложенная нами, получила название «метод вариации разностной частоты» и подробно описана в [3]. Исходя из ширины провала разностные частоты должны лежать в диапазоне 1–10 ГГц для работы в диапазоне κ от 0 до 5 м-1.
Заключение. По результатам анализа температурных, барических и изгибных эффектов в комплексе с исследованием оптомеханики ВБР с фазовым p-сдвигом, методами математического моделирования показана возможность получения как сверхузких окон прозрачности, так и достаточно широких, способных регистрировать изменения температуры в пределах 5–10°С при чувствительности решеток от 1 до 10 пм на 1°С, что вполне достаточно для построения систем автоматического регулирования. Проанализированы зависимости изменения спектральных характеристики фазированных решеток при приложении к ним равномерного и изгибного натяжения. Проведенные исследования показали, что окно прозрачности уширяется с сохранением градиента крутизны общего уширения решетки. При отсутствии воздействия ширина окна прозрачности составляла 0,01 нм, при кривизне изгиба решетки κ=5 м-1 ~ 0,16 нм. Использование ВБР с фазовым p-сдвигом позволит повысить разрешающую способность измерений температуры, линейного и изгибного натяжения в 10–50 раз, чувствительность – в 1,7–3,2 раза по сравнению с гомодинными методами измерений, использующими классические ВБР.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках проектной части государственного задания, выполняемого КНИТУ-КАИ на кафедре радиофотоники и микроволновых технологий и в научно-исследовательском институте прикладной электродинамики, фотоники и живых систем (программа «Радиофотоника», З.1962.2014/К).
Рецензенты:Морозов Г.А., д.т.н., профессор, директор Казанского филиала Поволжского государственного университета телекоммуникаций и информатики, г. Казань;
Анфиногентов В.И., д.т.н., профессор, профессор Казанского филиала Поволжского государственного университета телекоммуникаций и информатики, г. Казань.