В работе И.Н. Векуа [3, c.69]
в области ![]() , звездной относительно начала
координат, получена формула
, звездной относительно начала
координат, получена формула
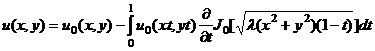 , (1)
, (1)
связывающая все регулярные (дважды – непрерывно дифференцируемые) решения метагармонического уравнения
![]() , (2)
, (2)
где ![]() – числовой параметр с гармоническими
функциями
– числовой параметр с гармоническими
функциями ![]() , то есть решениями в D уравнения
Лапласа
, то есть решениями в D уравнения
Лапласа
![]() .
(3)
.
(3)
В.И. Жегалов [5], К.Б. Сабитов [7] каждому регулярному решению уравнения с комплексным параметром
![]() (4)
(4)
сопоставили регулярное
решение ![]() уравнения Лаврентьева-Бицадзе
уравнения Лаврентьева-Бицадзе
![]() (5)
(5)
в области D через интегральное представление
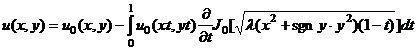 (6)
(6)
и указали метод
сведения решения краевых задач для уравнения (4) к соответствующим задачам для
уравнения (5). Там же получена теорема единственности решения задачи Трикоми
для уравнения (4) при ![]() .
.
В исследованиях К.Б.
Сабитова, Н.Г. Шмелёвой [8,9] проверена справедливость интегрального
представления (6) решений уравнения (4) с комплексным параметром ![]() и доказана его обратимость, а также
получена теорема единственности решения задачи Трикоми и доказана теорема
существования решения задачи Трикоми при более слабых ограничениях на граничные
данные. Также указаны приложения интегрального представления решений уравнения
(4) при решении задачи Франкля для этого уравнения.
и доказана его обратимость, а также
получена теорема единственности решения задачи Трикоми и доказана теорема
существования решения задачи Трикоми при более слабых ограничениях на граничные
данные. Также указаны приложения интегрального представления решений уравнения
(4) при решении задачи Франкля для этого уравнения.
В данной работе нами рассмотрено применение указанного метода к решению обобщенной задачи Трикоми для уравнения Лаврентьева-Бицадзе с вещественным параметром (4).
п.1. Рассмотрим уравнение
(4), где ![]() в области
в области ![]() , ограниченной кривой Ляпунова Г, лежащей
в полуплоскости y>0, с концами
в точках A=(0,0) и B=(1,0), и при y<0 прямой
, ограниченной кривой Ляпунова Г, лежащей
в полуплоскости y>0, с концами
в точках A=(0,0) и B=(1,0), и при y<0 прямой ![]() (kx+y=0, 0<k<1), и характеристикой
(kx+y=0, 0<k<1), и характеристикой ![]() (x-y=1).
(x-y=1).
Пусть ![]() ,
, ![]() .
.
Обобщенная задача Трикоми. Найти функцию u(x,y), удовлетворяющую условиям:
![]() ;
(7)
;
(7)
![]() ,
,
![]() ;
(8)
;
(8)
![]() ,
,
![]() ,
(9)
,
(9)
где x=x(s), y=y(s) – параметрические уравнения кривой Г, s – длина дуги отсчитываемая от точки В, l – длина кривой Г;
![]() ,
, ![]() ,
(10)
,
(10)
где 0<k<1, ![]() ,
, ![]() и
и ![]() –
заданные достаточно гладкие функции.
–
заданные достаточно гладкие функции.
Определение 1. Под регулярным в области ![]() решением
уравнения (4) понимается функция u(x,y), удовлетворяющая условиям
(7) и (8) обобщенной задачи Трикоми, и, кроме того, производные
решением
уравнения (4) понимается функция u(x,y), удовлетворяющая условиям
(7) и (8) обобщенной задачи Трикоми, и, кроме того, производные
![]() непрерывны в
непрерывны в ![]() ,
за исключением точек A, B,
где они могут обращаться в бесконечность порядка меньше единицы.
,
за исключением точек A, B,
где они могут обращаться в бесконечность порядка меньше единицы.
Заметим, что уравнение (6) однозначно обратимо относительно
функции ![]() в классе функций
в классе функций ![]() . Действительно, равенство (6) перепишем
в следующем виде:
. Действительно, равенство (6) перепишем
в следующем виде:
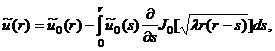 (11)
(11)
где ![]() ,
, ![]() ,
, ![]() .
.
Тогда, в силу результатов [3,10], решением уравнения (11) является функция вида:
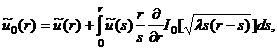 (12)
(12)
где ![]() – модифицированная
функция Бесселя.
– модифицированная
функция Бесселя.
Если функции ![]() и
и ![]() непрерывны в
непрерывны в ![]() ,
то равенства (11) и (12) являются формулами взаимного обращения [6]. Таким
образом, справедливо следующее:
,
то равенства (11) и (12) являются формулами взаимного обращения [6]. Таким
образом, справедливо следующее:
Теорема 1. Если функции ![]() и
и
![]() являются соответственно регулярными в
являются соответственно регулярными в ![]() решениями уравнений (5) и (4), то
между решениями этих уравнений существует взаимно-однозначное соответствие, которое устанавливается по
формулам (11) и (12).
решениями уравнений (5) и (4), то
между решениями этих уравнений существует взаимно-однозначное соответствие, которое устанавливается по
формулам (11) и (12).
Теорема 2. Пусть кривая Г – из класса Ляпунова, и на ней отсутствуют точки, при переходе котoрых ![]() меняет
знак, а
меняет
знак, а ![]() . Тогда, если в классе регулярных
в
. Тогда, если в классе регулярных
в ![]() решений уравнения (4)
существует решение обобщенной задачи Трикоми, то оно единственно при всех
решений уравнения (4)
существует решение обобщенной задачи Трикоми, то оно единственно при всех![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству
![]() ,
,
где ![]() – единичный вектор внутренней нормали к границе
области,
– единичный вектор внутренней нормали к границе
области, ![]() ,
, ![]() .
.
Предварительно отметим, что в работе [7] для уравнения типа Чаплыгина
![]() (13)
(13)
доказана
Теорема 3 [3]. Пусть: 1)
кривая Г – из класса Ляпунова и
на ней отсутствуют точки, при переходе котoрых ![]() меняет
знак, а
меняет
знак, а ![]() ; 2)
; 2) ![]() ; 3) функция
; 3) функция
![]() такова, что существует решение
такова, что существует решение ![]() уравнения Риккати
уравнения Риккати
![]() (14)
(14)
на интервале ![]() из
класса
из
класса ![]() , удовлетворяющее условию
, удовлетворяющее условию ![]() ;
; ![]() и
и ![]() при y<0.
при y<0.
Тогда, если в классе регулярных в D решений уравнения (13) существует решение обобщенной задачи Трикоми, то оно единственно.
Доказательство теоремы 2.
Умножим уравнение (4) на sgny. Тогда оно примет вид:
![]() . (15)
. (15)
Теперь покажем, что при некоторых условиях на ![]() для уравнения (15) справедлива теорема
3. В случае уравнения (15): K(y)=sgn y,
для уравнения (15) справедлива теорема
3. В случае уравнения (15): K(y)=sgn y,
![]() .
.
Пусть ![]() . Решением
уравнения Риккати (14) на интервале
. Решением
уравнения Риккати (14) на интервале ![]() является
функция
является
функция ![]() , где постоянная k определяется из условий
, где постоянная k определяется из условий ![]() ,
, ![]() .
Отсюда вытекает, что функция
.
Отсюда вытекает, что функция ![]() ,
удовлетворяющая условиям теоремы 3, существует, если
,
удовлетворяющая условиям теоремы 3, существует, если ![]() .
.
При ![]() теорему 3 прямо не
удается использовать для получения единственности решения обобщенной задачи
Трикоми для уравнения (4). В этом случае введем функцию
теорему 3 прямо не
удается использовать для получения единственности решения обобщенной задачи
Трикоми для уравнения (4). В этом случае введем функцию
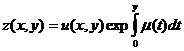 ,
,
которая является решением уравнения
![]() ,
(16)
,
(16)
где функция ![]() определяется как решение
уравнения Риккати
определяется как решение
уравнения Риккати
![]() . (17)
. (17)
Пусть
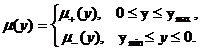
Тогда из уравнения (17) получим
![]() ,
, ![]() ,
,
![]()
![]() ,
,
где постоянная k находится из условий
![]()
![]() .
.
На плоскости (x,y)
введем новые переменные ![]()
![]() ,
, 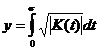 ,
(18)
,
(18)
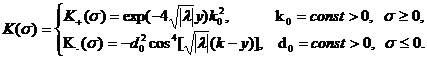
Тогда уравнение (16) принимает вид
![]() .
(19)
.
(19)
Следовательно, обобщенная задача Трикоми для уравнения (4)
при ![]() сведена к обобщенной задаче Трикоми для
уравнения (19) на плоскости
сведена к обобщенной задаче Трикоми для
уравнения (19) на плоскости ![]() , но с
разрывным условием склеивания на линии изменения типа
, но с
разрывным условием склеивания на линии изменения типа ![]() :
: ![]() .
.
Из доказательства теоремы 3 следует, что для решения однородной обобщенной задачи Трикоми для уравнения (19) справедливо неравенство
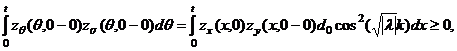 (20)
(20)
при ![]() . Теперь для
справедливости теоремы 3 для уравнения (17) достаточно показать, что
. Теперь для
справедливости теоремы 3 для уравнения (17) достаточно показать, что
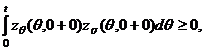
![]() .
.
Действительно, из (18) и (20) имеем
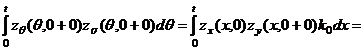
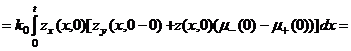
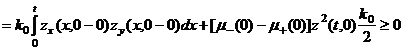 ,
,
если ![]() Последнее
неравенство справедливо, когда
Последнее
неравенство справедливо, когда ![]() ,
, ![]()
Отсюда получим условие относительно параметра ![]() . Тем самым теорема 2 доказана.
. Тем самым теорема 2 доказана.
п.2. Докажем существование
решения задачи (7) – (10). Интегральное представление (6) в классе регулярных
в ![]() решений уравнения (4) позволяет свести
решение задачи (7) – (10) к решению обобщенной задачи Трикоми для уравнения (5)
в области
решений уравнения (4) позволяет свести
решение задачи (7) – (10) к решению обобщенной задачи Трикоми для уравнения (5)
в области ![]() с пока неизвестными краевыми
условиями
с пока неизвестными краевыми
условиями ![]() на Г и
на Г и ![]() на АС.
на АС.
Прежде всего, заметим, что
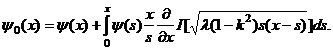
В самом деле, подставим в интегральный член формулы (6) значение
![]()
![]()
где ![]() , являющееся решением
обобщенной задачи Дарбу для уравнения (5) в области
, являющееся решением
обобщенной задачи Дарбу для уравнения (5) в области ![]() с
данными:
с
данными: ![]()
![]() ;
;
![]() ,
, ![]() .
Если известно, что
.
Если известно, что ![]() ,
, ![]() ,
, ![]() ,
функции
,
функции ![]() и
и ![]() ограничены
по n при любом фиксированном x.
Получим
ограничены
по n при любом фиксированном x.
Получим
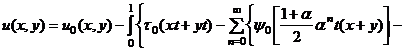
![]() (21)
(21)
Теперь в равенстве (21), полагая y=-kx с учетом граничного условия ![]() на АС, будем иметь
на АС, будем иметь
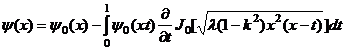
или
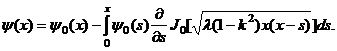
Получено интегральное уравнение Вольтерра второго рода. Его решение в силу [6] имеет вид
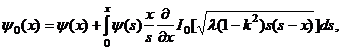 (22)
(22)
где ![]() обладает той же
гладкостью, что и
обладает той же
гладкостью, что и ![]() .
.
Теперь найдем функцию ![]() с
помощью аналогичных рассуждений, как и в случае решения задачи Трикоми [6].
Функцию
с
помощью аналогичных рассуждений, как и в случае решения задачи Трикоми [6].
Функцию ![]() в области
в области ![]() определим как решение задачи Хольмгрена
для уравнения Лапласа с граничными условиями:
определим как решение задачи Хольмгрена
для уравнения Лапласа с граничными условиями:
![]()
![]() , (23)
, (23)
![]() ,
, ![]() .
(24)
.
(24)
Известно [12, гл. 4;5], что решение этой задачи с граничными условиями (23) и (24) методом Грина выписывается в явном виде:
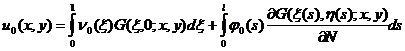 , (25)
, (25)
где ![]() – функция Грина задачи Хольмгрена
уравнения Лапласа,
– функция Грина задачи Хольмгрена
уравнения Лапласа, ![]() ,
, ![]() – функция гармоническая в области
– функция гармоническая в области ![]() по координатам точек
по координатам точек ![]() и (x,y)
строится аналогично [12, c.184].
и (x,y)
строится аналогично [12, c.184].
Отсюда найдем
соотношение между функциями ![]() и
и ![]() . Полагая в (25) y=0, будем иметь
. Полагая в (25) y=0, будем иметь
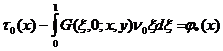 ,
, ![]() ,
(26)
,
(26)
где
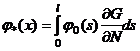 ,
, ![]() .
.
Далее, на основании решения задачи Дарбу для уравнения (5) с
данными ![]() ,
, ![]() ,
,
![]()
![]() найдем
второе соотношение между функциями
найдем
второе соотношение между функциями ![]() и
и ![]() на отрезке АВ, привнесенное из гиперболической части смешанной области
на отрезке АВ, привнесенное из гиперболической части смешанной области ![]() :
:
![]()
![]() (27)
(27)
Исключая ![]() из (26) и
(27), получаем интегральное уравнение для определения функции
из (26) и
(27), получаем интегральное уравнение для определения функции ![]()
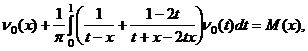 (28)
(28)
где
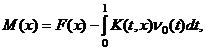
![]()
![]()
![]()
Как известно, [12, с.312] в случае, когда кривая Г
оканчивается сколь угодно малой длины дугами полуокружности, ядро K(t,x) непрерывно дифференцируемо в квадрате
![]() , за исключением точек (0,0) и (1,1), где
оно имеет слабую особенность.
, за исключением точек (0,0) и (1,1), где
оно имеет слабую особенность.
Если ![]() ,
, ![]() и
в малой окрестности точек 0 и l
удовлетворяет условию Гельдера с показателем
и
в малой окрестности точек 0 и l
удовлетворяет условию Гельдера с показателем ![]() из
[1/2,1], то функция
из
[1/2,1], то функция ![]() и при
и при ![]() и
и ![]() имеет
оценку
имеет
оценку ![]()
Теперь на основании отмеченного выше нетрудно получить решение сингулярного интегрального уравнения (28), которое непрерывно дифференцируемо в интервале (0,1) и на его концах может допускать интегрируемые особенности порядка меньше единицы. Такое решение методом Карлемана-Векуа определяется по формуле
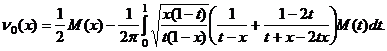
Вместо функции M(x), подставляя ее выражение, получим интегральное уравнение Фредгольма второго рода
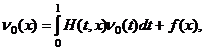 (29)
(29)
где
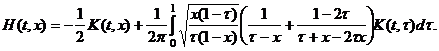 (30)
(30)
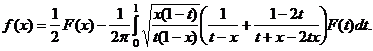 (31)
(31)
Ядро H(t,x), как показано [12, c.317], может
иметь особенности в точках (0,0) и (1,1) порядка меньше, чем 1/2. Свободный
член f(x) ограничен вблизи точки
0, может иметь особенность порядка не выше 1/2 в окрестности точки 1 и
принадлежит классу ![]()
Теперь покажем, что соответствующее уравнению (29) однородное уравнение
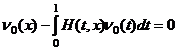 (32)
(32)
имеет только нулевое
решение. Действительно, если ![]() и
и ![]() , то в силу теоремы 2 о единственности
решения обобщенной задачи Трикоми для уравнения (4)
, то в силу теоремы 2 о единственности
решения обобщенной задачи Трикоми для уравнения (4) ![]() в
в ![]() .
Тогда из формулы обращения (12) следует
.
Тогда из формулы обращения (12) следует ![]() в
в ![]() .
Отсюда вытекает, что
.
Отсюда вытекает, что ![]() на интервале (0,1), т.е. однородное
уравнение (32) имеет только нулевое решение в классе
на интервале (0,1), т.е. однородное
уравнение (32) имеет только нулевое решение в классе ![]() . Тогда на основании теории Фредгольма
решение уравнения (27) может быть записано в виде:
. Тогда на основании теории Фредгольма
решение уравнения (27) может быть записано в виде:
 (33)
(33)
где R(t,x) – резольвента ядра H(t,x).
Далее, подставляя (33) в (25) и меняя пределы интегрирования, получим
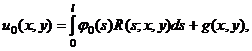 (34)
(34)
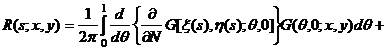
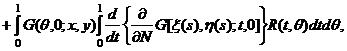
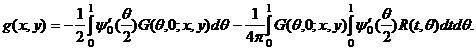
Функцию ![]() , заданную формулой (34), подставим в
интегральный член формулы (6) при y>0,
и, снова меняя пределы интегрирования, будем иметь
, заданную формулой (34), подставим в
интегральный член формулы (6) при y>0,
и, снова меняя пределы интегрирования, будем иметь
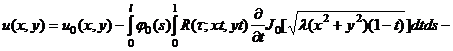 (35)
(35)
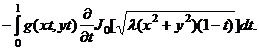
Переходя в (35) к
пределу при ![]() , получим
, получим
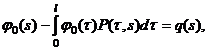 (36)
(36)
где
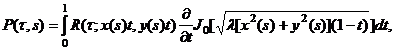
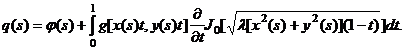
Поскольку ядро ![]() непрерывно в квадрате
непрерывно в квадрате ![]() и правая часть q(s) непрерывна на [0,1], то к уравнению
(36) применима теория Фредгольма. В силу теоремы 2 о единственности решения
обобщенной задачи Трикоми для уравнения (4) и формулы обращения (12)
соответствующее однородное интегральное уравнение
и правая часть q(s) непрерывна на [0,1], то к уравнению
(36) применима теория Фредгольма. В силу теоремы 2 о единственности решения
обобщенной задачи Трикоми для уравнения (4) и формулы обращения (12)
соответствующее однородное интегральное уравнение

имеет только нулевое решение. Тогда на основании альтернативы Фредгольма неоднородное интегральное уравнение (36) имеет единственное решение в классе непрерывных на [0,l] функций.
Таким образом, доказана следующая
Теорема 4. Если ![]() и в достаточно малой окрестности точек s=0 и s=l
удовлетворяет условию Гельдера с показателем
и в достаточно малой окрестности точек s=0 и s=l
удовлетворяет условию Гельдера с показателем
![]() ,
, ![]()
![]() ,
, ![]() и
кривая Г и
и
кривая Г и ![]() удовлетворяют условиям теоремы
2, то существует единственное решение
обобщенной задачи Трикоми для уравнения(4) в классе его регулярных в
удовлетворяют условиям теоремы
2, то существует единственное решение
обобщенной задачи Трикоми для уравнения(4) в классе его регулярных в ![]() решений, которое определяется формулой (11), где
решений, которое определяется формулой (11), где ![]() – решение обобщенной задачи Трикоми для
уравнения (5) с граничными
условиями
– решение обобщенной задачи Трикоми для
уравнения (5) с граничными
условиями ![]() на Г,
на Г, ![]() на АС а
на АС а ![]() есть решение интегрального уравнения Фредгольма (36),
есть решение интегрального уравнения Фредгольма (36), ![]() находится по
формуле (22).
находится по
формуле (22).
Заключение
Полученные в исследовании результаты имеют теоретический характер и обладают новизной. Основные положения разрабатываемой проблемы представлены в виде докладов [10-13] на научных конференциях. Они могут быть использованы при дальнейшей разработке теории краевых задач для уравнений смешанного типа.
Авторы выражают благодарность Камилю Басыровичу Сабитову, доктору физико-математических наук, профессору, за высказанные предложения и замечания при организации исследования проблемы решения краевых задач.
Рецензенты:Кризский В.Н., д.ф.-м.н., профессор, Стерлитамакский филиал Башкирского Государственного университета, г. Стерлитамак;
Шулаев Н.С., д.т.н., профессор, филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Стерлитамак.



