Известно, имитационные характеристики обучающих комплексов по подготовке операторов транспортных систем во многом определяются латентным периодом формирования оператором управляющих воздействий, наличием люфтов в канале управления и др. [4, 7, 8].
Наличие запаздывания усложняет выбор численных методов для имитационного моделирования объекта управления эргатической системы. Действительно, рассмотрим систему второго порядка:
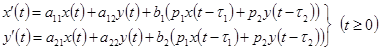
![]()
При очень малых ![]() таких, что ими можно пренебречь (достаточная точность интегрирования обеспечивается уже при шаге
таких, что ими можно пренебречь (достаточная точность интегрирования обеспечивается уже при шаге ![]() ), придем к задаче без запаздывания:
), придем к задаче без запаздывания:
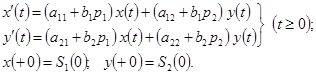
При больших запаздываниях шаг интегрирования должен соразмеряться с запаздыванием; при ![]() , можно принять
, можно принять ![]() , где
, где ![]() .
.
В векторно-матричной форме имеем:
![]()
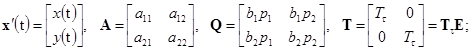
![]() – оператор сдвига:
– оператор сдвига: ![]()
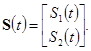
При ![]() задача сводится к определению решения:
задача сводится к определению решения:
![]() ;
;
возможно уменьшение шага (вместо ![]() принять шаг
принять шаг ![]() , где
, где ![]()
![]() ).
).
При использовании метода Рунге – Кутта второго порядка точности:
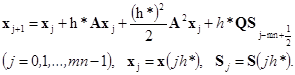
При ![]() , исходная задача с запаздыванием решается приближенно с шагом
, исходная задача с запаздыванием решается приближенно с шагом ![]() . Здесь метод Рунге – Кутта принимает вид:
. Здесь метод Рунге – Кутта принимает вид:
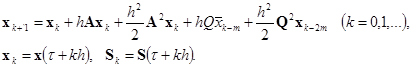
В силу непрерывной зависимости корректно поставленной задачи от запаздывания при небольших значениях запаздывания зависимость между шагом ![]() , частотой
, частотой ![]() , декрементом затухания
, декрементом затухания ![]() и заданной точностью
и заданной точностью ![]() (при фиксировании остальных параметров системы) остается близкой к той зависимости, которая существует для систем без запаздывания. В остальных случаях для получения требуемых имитационных характеристик обучающего комплекса выбор шага при интегрировании уравнений движения объекта должен осуществляться с учетом величин запаздывания в различных контурах управления. Действительно, рассмотрим моделирование короткопериодической составляющей продольного движения транспортного самолета. В этом случае задача сводится к решению уравнения:
(при фиксировании остальных параметров системы) остается близкой к той зависимости, которая существует для систем без запаздывания. В остальных случаях для получения требуемых имитационных характеристик обучающего комплекса выбор шага при интегрировании уравнений движения объекта должен осуществляться с учетом величин запаздывания в различных контурах управления. Действительно, рассмотрим моделирование короткопериодической составляющей продольного движения транспортного самолета. В этом случае задача сводится к решению уравнения:
![]() ,
,
где ![]() – двумерная вектор-функция,
– двумерная вектор-функция, ![]() – квадратная матрица. Задача определяется шестью параметрами: компонентами матрицы
– квадратная матрица. Задача определяется шестью параметрами: компонентами матрицы ![]() и вектора
и вектора ![]() .
.
В случае мнимых корней ![]() характеристического уравнения решение задачи имеет вид:
характеристического уравнения решение задачи имеет вид:
![]()
где ![]() – линейно независимые векторы.
– линейно независимые векторы.
При приближенном решении численным методом с шагом ![]() для погрешности вычисления методом Рунге – Кутта второго порядка точности справедливо:
для погрешности вычисления методом Рунге – Кутта второго порядка точности справедливо:
![]() ,
,
где ![]()
Так как ![]() , то
, то ![]()
Имеем:
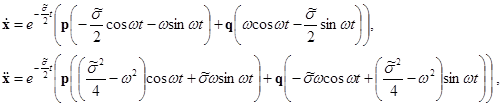
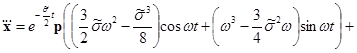
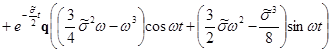 .
.
Очевидно, ![]() . Поэтому в качестве параметров, определяющих систему, можно взять следующие шесть:
. Поэтому в качестве параметров, определяющих систему, можно взять следующие шесть: ![]() и компоненты векторов
и компоненты векторов ![]() .
.
С учетом:
![]()
получим:
![]()
Из
![]()
следует:
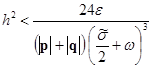 .
.
Как видим, при фиксированных компонентах векторов ![]() и
и ![]() имеем:
имеем:
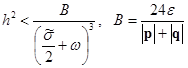
и шаг ![]() определяется декрементом затухания
определяется декрементом затухания![]() и частотой
и частотой ![]() (зависимость для
(зависимость для ![]() приводится на рис. 1).
приводится на рис. 1).
В рассматриваемом случае полоса рабочих частот ограничена сверху ![]() 10с-1, снизу –
10с-1, снизу – ![]() 2с-1; безразмерный коэффициент затухания
2с-1; безразмерный коэффициент затухания ![]() изменяется в пределах от 0,4 до 0,9.
изменяется в пределах от 0,4 до 0,9.
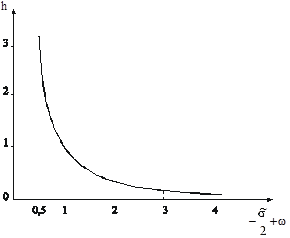
Рис.1 .Зависимость шага интегрирования h от ![]()
С ростом ![]() величина:
величина:
![]()
уменьшается (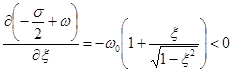 ); допустимый шаг
); допустимый шаг ![]() растет с ростом
растет с ростом ![]() .
.
Не случайно при настройке тренажеров возникает стремление увеличить коэффициент демпфирования при достаточно больших реальных значениях ![]() (приводит к искажению характеристик самолета: увеличение
(приводит к искажению характеристик самолета: увеличение ![]() вызывает соответствующее уменьшение собственной частоты
вызывает соответствующее уменьшение собственной частоты ![]() ). Точка
). Точка ![]() в областях равных оценок пилотажных характеристик сдвигается (оценка пилотажных характеристик тренажера улучшается, а соответствие самолета и модели – ухудшается).
в областях равных оценок пилотажных характеристик сдвигается (оценка пилотажных характеристик тренажера улучшается, а соответствие самолета и модели – ухудшается).
Для системы без затухания (![]() ):
):
![]()
Для отношения максимально допустимых шагов для систем с собственными частотами ![]() и
и ![]() (оценка сверху) справедливо:
(оценка сверху) справедливо:
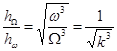 ;
;
В полосе рабочих частот от 2 рад/сек. до 10 рад/сек. допустимый шаг интегрирования изменяется более чем в 10 раз.
Аналогичную оценку для шага ![]() можно получить, исходя из условия:
можно получить, исходя из условия:
![]() ;
;
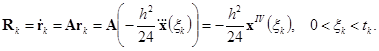
Имеем
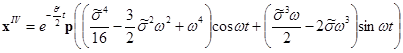 +
+
+ ![]()
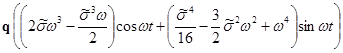 ;
;
![]() ;
;
![]() .
.
![]()
Откуда:
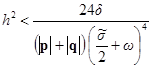 или
или 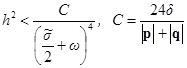 .
.
Если![]() , то
, то ![]() .
.
Максимальные значения шагов ![]() и
и ![]() , полученные по условиям
, полученные по условиям ![]() и
и![]() , соответственно приводятся на рис. 2 (принято В = С = 1).
, соответственно приводятся на рис. 2 (принято В = С = 1).
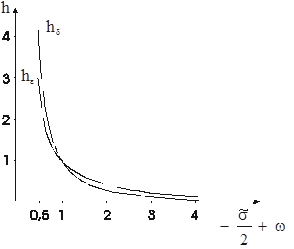
Рис. 2. Зависимость шага интегрирования h от e и d
Полученные оценки использовались при разработке имитационных моделей объекта управления транспортной эргатической системы с интегрированием уравнений движения в реальном масштабе времени с обновлением начальных условий и переменных параметров на каждом шаге интегрирования [1…3, 5, 6].
Рецензенты:
Родионов Ю. В., д.т.н., декан автомобильно-дорожного института ПГУАС, профессор, заведующий кафедрой «Эксплуатация автомобильного транспорта», г. Пенза;
Логанина В. И., д.т.н., профессор, зав. кафедрой «Управление качеством и технологии строительного производства» Пензенского государственного университета архитектуры и строительства, г. Пенза.



