Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Исследование системных объектов различной природы в современных условиях неразрывно связано с имитационным моделированием [5, 6], которое позволяет создавать разнообразные детерминировано-вероятностные функциональные зависимости, имитирующие работу заданной системы с помощью генератора случайных чисел. Получаемая исследователем информация для анализа программируемых закономерностей представляет собой массивы эмпирических данных о значениях независимых и зависимых переменных. Построение математической модели, устанавливающей взаимосвязь искомых и известных величин, предоставляет возможность провести тестирование программы автоматических вычислений на адекватность отражения существенных закономерностей, присущих исследуемому объекту, проявляющему системные свойства. Если независимой переменной выступает время, то представляется целесообразным рассматривать величины, изменяемые во времени, как временные ряды.

Подбор линейной или нелинейной модели тренда для описания закономерностей эмпирических данных подробно рассматривается в работах [1, 2, 3, 7, 8]. Определению параметров тригонометрического тренда, значения уровней которых повторяются с некоторым периодом, для исследования периодических процессов уделяется недостаточное внимание. Это связано прежде всего с трудоемкостью вычислительных процедур, обеспечивающих нахождение параметров исследуемых закономерностей. Функционирование многих технических систем или устройств рассматривается как колебательное движение, математической моделью которых выступают разнообразные композиции тригонометрических функций, поэтому представляется целесообразным систематизировать информацию о составлении тригонометрического тренда и проверке его статистической значимости. Иллюстрация содержания исследовательской деятельности, направленной на построение математической модели периодического процесса, представляет собой последовательное описание операций статистического анализа эмпирических данных, полученных при имитационном моделировании колебательного движения некоторой технической системы. Формирование исследовательских умений может включать следующие этапы: восприятие понятия тригонометрического тренда; получение эмпирических данных периодического процесса; составление точечной и интервальной оценки тригонометрического тренда; оценка качества уравнения тренда.

Результаты и обсуждение

Восприятие понятия тригонометрического тренда. Временным рядом (n – число уровней ряда) называется упорядоченная последовательность наблюдений над некоторыми явлениями, характер которых меняется во времени. Особенностью временного ряда является то, что порядок последовательности t1, t2, …, tn существенен для анализа, а время выступает как один из определяющих факторов [1, 2, 3, 8].

Математическая модель точечной оценки тригонометрического тренда имеет следующий вид [2]:

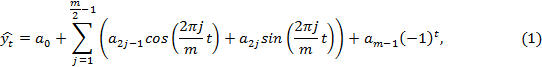
где ŷt – моделируемое значение yt; a0, a2j-1, a2j – параметры тренда, j = 1, …, m/2 – 1; m – период тренда.

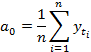
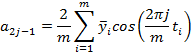
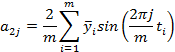
Параметры тригонометрического тренда a0, a2j-1, a2j определяются с помощью метода наименьших квадратов и вычисляются по формулам 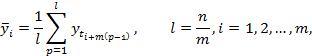[2]:

(2)

где l – количество периодов временного ряда.

Выделение периодической составляющей временного ряда осуществляется с помощью автокорреляционного анализа, который характеризует степень тесноты связи между наблюдениями и сдвинутыми относительно их на s уровней наблюдениями . Коэффициент автокорреляции rs, определяющий автокорреляционную зависимость между членами одного и того же ряда, но смещенными на s уровней, находится по формуле [1, 7]:

(3)

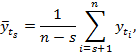
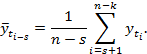
Если временной ряд имеет периодическую составляющую, то значения коэффициента автокорреляции rs, не меньшие, чем значение r1, будет повторяться через количество уровней, равных периоду. Наглядное представление автокорреляционной функции получают с помощью ее графика – автокоррелограммы [1, 7].

Оценка качества уравнения тренда определяется с помощью коэффициента детерминации R2, вычисление которого проводится по формуле:

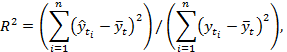
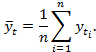(4)

Статистическая значимость уравнения тренда устанавливается по F-критерию (распределение Фишера–Снедекора) на уровне значимости α при числе степеней свободы k1, k2 (k1 = n, k2 = n – k – 1, k – количество параметров ai, i = 1,…, m – 2). Связь между значениями уровней временного ряда и временем считается статистически значимой, если выполняется неравенство [2, 3]:

Fнабл > Fкр(α; k1, k2). (5)

Значение критической точки Fкр(α; k1, k2) на уровне значимости α при числе степеней свободы k1, k2 определяется по таблице распределения Фишера–Снедекора, а наблюдаемое значение Fнабл критерия Фишера–Снедекора вычисляется по формуле [2, 3]:

Уравнения нижней и верхней границ интервальной оценки ( тренда составляются с учетом абсолютной погрешности Δ по следующим формулам:

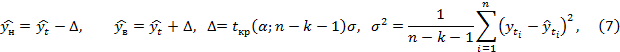
где – значение критической точки распределения Стьюдента на уровне значимости α при числе степеней свободы n – k – 1; σ2 – дисперсия случайной составляющей.

Получение эмпирических данных периодического процесса. Колебательное движение некоторой технической системы моделировалось на основе математической модели, параметры которой подбираются с помощью программного обеспечения ЭВМ. Использование в программе генератора случайных значений имитировало проявление детерминировано-вероятностных закономерностей. В ходе проведения вычислительного эксперимента фиксировались значение величины f(t), изменяющейся во времени (рис. 1, табл. 1).

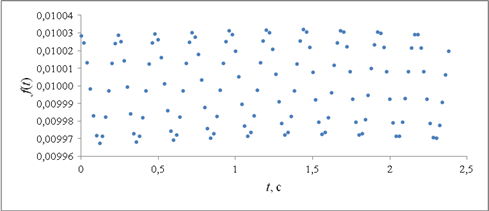
Рис. 1. Графическое представление эмпирических данных

Таблица 1

Значения величины f(t)

Составление точечной и интервальной оценок тригонометрического тренда. Для выявления периодической составляющей вычисляются по формуле (3) с использованием функции «КОРРЕЛ» электронных таблиц Excel [4] 16 значений коэффициента автокорреляции, строится автокоррелограмма (рис. 2) и определяется период тригонометрического тренда (m = 12).

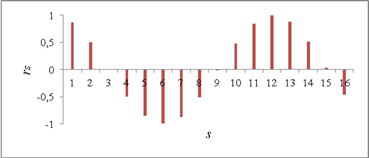
Рис. 2. Автокоррелограмма эмпирических данных

Наибольшее значение амплитуды тригонометрического тренда наблюдается у первой гармоники, поэтому в практических случаях часто ограничиваются построением математической модели f*(t) с одной гармоникой по формуле (1), учитывая, что j = 1. Графическая модель точечной оценки тренда представлена на рисунке 3, а ее уравнение имеет вид:

где t0 – начальный момент времени, Δt – шаг изменения времени.

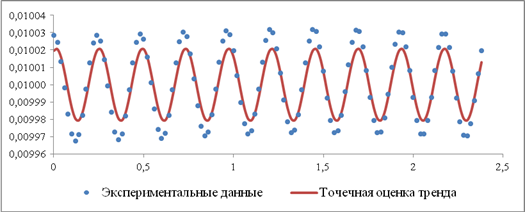
Рис. 3. Точечная оценка тренда

В формуле (8) учтена особенность того, что отсчет времени может начинаться с t0 и изменяться с шагом Δt , в отличие от того, что отсчет уровней временного ряда начинается от единицы и изменяется с шагом, также равным единице. Параметры a0, a1, a2 функции f*(t) находятся для n = 120 и l = 10 по формуле (2) и принимают следующие значения:

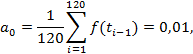
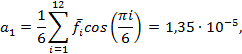
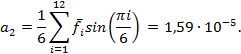
Средние значения i-ого уровня всех l периодов вычисляется по формуле:

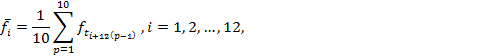
а их множество представлено в таблице 2. В данном эксперименте t0 = 0, Δt = 0,02 с.

Таблица 2

Средние значения всех уровней периода тренда

Интервальная оценка (f*(t) – Δ; f*(t) + Δ) тригонометрического тренда определяется по t-критерию (распределение Стьюдента) на уровне значимости α = 0,05 при числе степеней свободы 117 по формуле (7). Уравнения нижней f*н(t) и верхней f*в(t) границ интервальной оценки имеют вид:

Графические модели уравнений f*н(t) и f*в(t) представлены на рисунке 4.

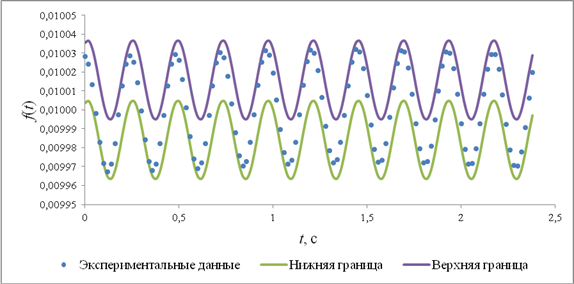
Рис. 4. Интервальная оценка тригонометрического тренда

Интервал (f*(t) – Δ; f*(t) + Δ) накрывает все эмпирические данные (рис. 4), следовательно, ограничение одной гармоникой тригонометрического тренда успешно описывает результаты проведенного вычислительного эксперимента.

Оценка качества уравнения тренда. Коэффициент детерминации R2 вычисляется по формуле (6) и в данном исследовании принимает значение, равное 0,47. Значимость R2, определяемая по F-критерию (распределение Фишера—Снедокора), характеризует возможность применения уравнения тренда f*(t) для описания рассматриваемого периодического процесса. По результатам вычислений устанавливается, что связь между значениями функции f*(t), разделенными Δt (значениями уровней временного ряда), статистическая значима на уровне α = 0,05 при числе степеней свободы k1 = 120 и k2 = 117, так как неравенство (5) выполняется (Fнабл = 52,68; Fкр(0,05; 120; 117) = 1,35). Математическая модель интервальной оценки функциональной зависимости f*(t) адекватно отображает взаимосвязи совершаемого некоторой технической системой колебательного движения f(t), информация о котором представлена в табличной форме (таблица 1).

Заключение

Представление тригонометрического тренда двумя и более гармониками позволяет получить более точные результаты по моделированию периодического процесса. Количество гармоник, которое включается в математическую модель, определяется допустимой точностью функционирования заданной технической системы. При этом обязательно учитывается условие о накрытии интервальной оценкой составляемой функциональной зависимости размаха отклонений амплитуды колебаний. Предложенные этапы построения тригонометрического тренда могут использоваться в учебно-исследовательской деятельности студентов технических направлений подготовки при изучении дисциплин профессионального цикла образовательной программы.

Рецензенты:

Стружанов В.В., д.ф.-м.н., профессор, главный научный сотрудник Института машиноведения УрО РАН, г. Екатеринбург;

Титов С.С., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная математика и техническая графика» Уральской государственной архитектурно-художественной академии, г. Екатеринбург.