В настоящее время при профессиональной подготовке водительского состава повсеместное распространение получили автомобильные тренажеры, обеспечивающие полную безопасность и высокую экономичность процессов обучения. К сожалению, ряд модификаций обладает условностью восприятия дорожной обстановки, связанной либо со статичностью кабин, или жесткой программой имитируемой ситуации, не связанной с управляющими действиями обучаемого. Поэтому используются ситуационные автотренажеры, позволяющие значительно повысить эффективность обучения. В них управление в процессе обучения производится вычислительным устройством, связанным с системой имитации дорожной обстановки. Предусматривается возможность воспроизведения неожиданного появления пешехода на проезжей части, внезапный выезд на перекресток других транспортных средств и т.д.
Одной из важнейших задач при создании тренажных и обучающих комплексов [1,4,5,6,7,9] для подготовки операторов мобильных систем является установление и последующее ранжирование стимулов (информативных сигналов), на основе которых человек-оператор и производит формирование управляющих воздействий (реакции на входные сигналы). Она тесно связана с определением психофизиологического статуса оператора (устанавливается на основе клинико-экспериментальной оценки). Обе задачи здесь решаются на основе рассмотрения человека-оператора как элемента многомерного информационного канала и по существу сводятся к решению основной задачи статистической теории распознавания образов. Вторая задача на первом этапе решается в условиях предельного случая (для контингента с выраженными характеристиками принятия решения; такой подход особенно часто используется в психиатрии). Участие в исследованиях практических психологов и психиатров в значительной степени позволили оценить комплексы стимулов при принятии решений операторами для решения конкретных задач.
Математическое моделирование замкнутой человеко-машинной системы (эргатическая система) существенно усложняется в связи с действием в ней организмического принципа (оператор достраивает свои параметры организмически оптимально). Практически авторами решалась частная задача идентификации с использованием результатов данных нормального функционирования. В частности, определялись [4,9]:
-
распределение вероятностей дискретных значений фазовых координат,
-
условные вероятности дискретных значений управляющих воздействий,
-
числовые характеристики фазовых координат и управляющих воздействий, как случайных функций,
-
меры зависимостей между управляющими воздействиями и значениями выходных координат,
-
характеристики каналов управления, как дискретных информационных каналов, в том числе характеристики дублирований и взаимодействия в передаче стимулов (выходных координат) при выборе соответствующих реакций,
-
корреляционные функции и спектральные характеристики фазовых координат и управляющих воздействий.
Обычно в качестве количественных характеристик зависимостей случайных величин рассматриваются смешанные центральные моменты и их аналоги, в частности, коэффициенты корреляции. Однако эти характеристики в ряде случаев слабо связаны с зависимостью случайных величин; правда, в некоторых случаях получаются вполне удовлетворительные результаты (например, в случае линейной функциональной зависимости).
Поэтому использовались количественные характеристики, на наш взгляд, более отражающие суть явлений. Это подтвердилось при исследовании ряда задач распознавания образов и диагностики. В качестве меры зависимости 
случайного события 
от случайного события 
принималась условная вероятность 
; в общем случае 
. Мерой зависимости события от событий 
рассматривался вектор (
,
,…,
). В случае, когда 
– независимые события и 
, то рассматривается как линейная комбинация событий :
;
здесь речь идет не о линейной функциональной зависимости от (может быть нелинейной и более сложной). Для дискретной случайной величины в качестве меры зависимости принималась 
, 
– значения случайных величин и соответственно, 
– условная вероятность события 
относительно события 
,
– вероятность события . При вычислении по статистическим данным (по выборке объема N) полезно вычислять как по всей выборке, так и по ее репрезентативным частям (с минимальным пересечением) и взять среднее значение.
Для селекции информативных сигналов и решения связанной с этим задачи диагностики использовался метод последовательного распознавания. В последовательной процедуре вместо одного порога, как в классической процедуре, задаются два порога: проверяемая гипотеза (основная или нулевая) 
и альтернативная гипотеза (конкурирующее с ней предположение) 
. Вследствие ограниченности выборки, полученной из генеральной совокупности, по которой проверяется гипотеза, возможны ошибки, как в ту, так и в другую сторону. В небольшой доле a случаев гипотеза может оказаться отвергнутой, в то время как на самом деле она является справедливой, или, наоборот, в доле b случаев принимается гипотеза , в то время как она является ошибочной, а справедливой оказывается .
Выбор величины уровня значимости a (ошибка первого рода – вероятность a ошибочного отклонения гипотезы) зависит от сопоставления потерь вследствие ошибочных заключений (при a = 0,05 в 5 случаях из 100 ошибочно отвергается гипотеза); вероятность b принятия неправильной гипотезы – ошибка второго рода. Чем весомее потери от ошибочного отказа от, тем меньше выбирается a (например, целесообразней признать доброкачественную опухоль онкологическим заболеванием, чем наоборот).
Рассмотрим подмножество выборок, которые приводят к гипотезе H1 , и определим вероятность того, что последовательный процесс закончится принятием гипотезы H1 (отклонением). Эта вероятность равна или меньше a в случае, когда на самом деле имеет место гипотеза, и равна или меньше 1 - b, если на самом деле имеет место гипотеза. Последнее положение следует из того, что по определению вероятность принятия , когда верна, равна b. Доказана сходимость последовательной процедуры за конечное число шагов n, поэтому можно утверждать, что вероятность отклонения (принятия ), когда верна , должна быть равна 1 - b. На каждом шаге (включая последний) справедливо соотношение 
, откуда следует 
или 
; аналогично 
. Так что: 0 < 
£ B £ 1 £ A £ 
.
Практически последовательная процедура будет завершена, когда выборка перестанет попадать в область, определяемую двойным неравенством 
.
Неотрицательный результат статистической проверки гипотезы не означает, что высказанное предположительное утверждение является наилучшим, единственно подходящим. Из этого лишь следует, что она не противоречит имеющимся выборочным данным. При этом таким же качеством могут обладать, наряду с, и другие гипотезы [8].
Вероятность каждого из возможных состояний 
объекта по методу последовательного распознавания (следует из формулы Байеса; позволяет установить вероятности состояний при наличии комплекса признаков (симптомов) 
, вообще говоря, зависимых) определяется в виде:
.
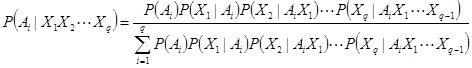При этом отношение
показывает, во сколько состояние 
вероятнее состояния 
.
Значение количества 
признаков устанавливается исходя из заранее выбранных допустимых уровней диагностических ошибок (после достижения порога или принимается решение: «состояние » или «состояние »). При последовательной процедуре распознавания для пары (
) возможны варианты: состояние 
, или 
, или имеющейся информации недостаточно для принятия решения с намеченным уровнем надежности (или существует промежуточное состояние между и ).
Для принятия одного из решений правая часть последнего равенства сравнивается с диагностическим порогом. Если 
– ошибочная диагностика состояния, 
– ошибка пропуска состояния; 
– ошибки второго и первого родов, то отношение вероятностей правильных и ошибочных диагнозов состояний равно 
. Аналогично отношение ошибочных и правильных диагнозов 
.
При 
принимается состояние ; при 
– состояние ; если 
, то последовательная процедура продолжается.
Если под классами понимать стили управления, а под признаками – источники информации, то решение задачи прогнозирования управления на тренажных комплексах легко осуществляется с использованием последовательной процедуры распознавания. Информация о взаимодействии двух входов 
и 
без учета дублируемой информации для различных классов управлений (по выходу) определится величиной
,
где 
, 
– соответственно количество информаций, передаваемых от 
к 
и парой 
к .
Эффективность использования комплексов для обучения операторов определяется имитационными характеристиками тренажера, определяющими формирование оператором управляющих воздействий.
Ограничимся эргатическими системами, для которых уравнения движения имеют вид:
(1)
или
, 
, 
,
;(1’)
, 
,
, 
, 
, 
, 
,
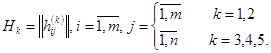(2)
В дискретной форме система (1’) представится в виде:
, 
,
, 
;(3)
,
,
, 
.
Справедливо
.(4)
Обычно всегда имеются синхронные измерения 
, полученные в условиях нормальной эксплуатации. Так что можно считать известными
,
.
Идентификация сводится к определению оценок компонент матрицы
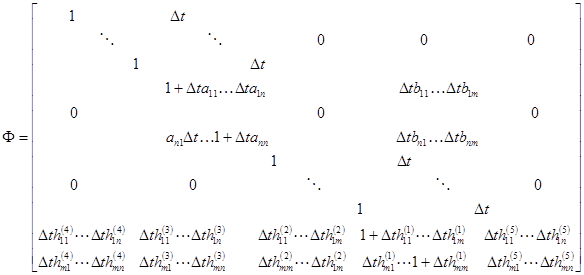
из условия 
, 
- оценка 
. Справедливо 
,
,
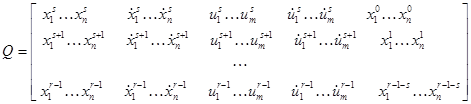
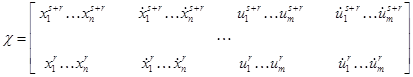т – символ транспонирования, 
.
Непосредственно из вида , ее блочной структуры, при заданной системе уравнений вида (1) появляется возможность идентифицировать параметры как объекта, так и оператора.
Рассматриваемый алгоритм многократно использовался [2,3] при параметрической идентификации как продольного, так и бокового движений эргатической системы (для короткопериодической составляющей ограничивались случаем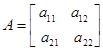 
, 
,
).
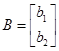Рецензенты:
Родионов Ю.В., д.т.н., профессор, заведующий кафедрой «Эксплуатация автомобильного транспорта», декан автомобильно-дорожного института ПГУАС, г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры «Информационно-вычислительные системы» Пензенского государственного университета архитектуры и строительства, г. Пенза.