В системе мер, направленных на достижение высокого качества продукции строительного назначения, важное место занимает контроль качества, включающий в себя:
– проверку качества строительных материалов и изделий, от которых зависит качество строительной продукции;
– систематическое проведение операционного контроля;
– проверку всех показателей качества готовой продукции на соответствие требованиям нормативных документов (ГОСТ, СНиП и т.д) и многое другое.
Контроль качества строительной продукции – это средство и составная часть процесса управления качеством. На современном этапе развития необходима разработка оперативной и действенной системы оценки качества [2,4]. Контроль качества продукции строительного назначения возможен при наличии научно обоснованной системы контроля качества и зависимости различных форм стимулирования работников от качества выпускаемой ими продукции.
Система контроля качества продукции представляет собой совокупность объектов и субъектов контроля, видов, методов и средств оценки качества продукции и профилактики дефектов на различных этапах жизненного цикла продукции (рис.1).
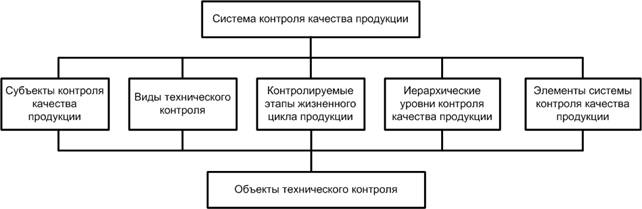
Рисунок 1. Структурно-функциональная модель системы контроля качества продукции
Результаты оценки качества строительной продукции требуют анализа для последующего регулирования наиболее значимых факторов, формирующих ее качество.
Методика проведения анализа контроля качества
В данной работе приводится одна из возможных мер анализа сотрудниками отдела качества проверки соответствия строительной продукции требованиям нормативной документации. В качестве примера проведем анализ для значений показателей оконных блоков, качество которых должно отвечать требованиям ГОСТ 24700-99. Нормативные значения показателей качества представлены в табл. 1.
Таблица 1
Нормативные значения показателей по ГОСТ 24700-99
|
Показатель качества продукции |
Сопротивление теплопередаче (не менее), м²·°С/Вт |
Звукоизоляция (не менее), дБА |
Светопропускание |
Воздухопроницаемость (не более), м³/(ч·м²) |
Отклонения
от
габаритных |
Прочность
угловых |
|
Нормативное значение (ГОСТ 24700-99) |
0,55 |
26 |
0,35-0,60 |
17 |
2 |
750 |
Результаты испытаний деревянных оконных блоков по шести показателям качества представлены в табл. 2.
Таблица 2
Результаты испытаний
|
№ |
Сопротивление теплопередаче, м² ·°С/Вт |
Звукоизоляция,
|
Светопропускание |
Воздухопроницаемость, м³/(ч·м²) |
Отклонение |
Прочность угловых |
|
1 |
0,55 |
26 |
0,35 |
14 |
1 |
750 |
|
2 |
0,56 |
27 |
0,36 |
15 |
2 |
750 |
|
3 |
0,58 |
25 |
0,37 |
16 |
0 |
750 |
|
4 |
0,57 |
26 |
0,38 |
14 |
1 |
750 |
|
5 |
0,57 |
26 |
0,40 |
18 |
2 |
750 |
|
6 |
0,53 |
27 |
0,41 |
18 |
0 |
750 |
|
7 |
0,55 |
28 |
0,45 |
14 |
0 |
750 |
|
8 |
0,54 |
29 |
0,34 |
14 |
1 |
740 |
|
9 |
0,56 |
30 |
0,50 |
15 |
2 |
750 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
10 |
0,55 |
25 |
0,51 |
15 |
1 |
730 |
|
11 |
0,54 |
26 |
0,42 |
17 |
1 |
740 |
|
12 |
0,55 |
27 |
0,58 |
17 |
1 |
743 |
13 |
0,55 |
28 |
0,59 |
16 |
0 |
750 |
|
14 |
0,57 |
29 |
0,60 |
17 |
2 |
750 |
|
15 |
0,58 |
25 |
0,34 |
15 |
1 |
750 |
|
16 |
0,59 |
27 |
0,35 |
15 |
3 |
750 |
|
17 |
0,59 |
28 |
0,42 |
15 |
2 |
750 |
|
18 |
0,58 |
26 |
0,45 |
16 |
2 |
750 |
|
19 |
0,57 |
27 |
0,46 |
17 |
1 |
750 |
|
20 |
0,57 |
25 |
0,48 |
16 |
0 |
750 |
|
21 |
0,57 |
26 |
0,35 |
15 |
3 |
750 |
|
22 |
0,56 |
27 |
0,36 |
18 |
2 |
750 |
|
23 |
0,55 |
25 |
0,37 |
16 |
1 |
740 |
|
24 |
0,55 |
28 |
0,34 |
18 |
3 |
750 |
|
25 |
0,53 |
29 |
0,35 |
17 |
2 |
740 |
|
26 |
0,54 |
30 |
0,36 |
16 |
1 |
750 |
|
27 |
0,55 |
25 |
0,38 |
15 |
2 |
750 |
|
28 |
0,56 |
26 |
0,40 |
15 |
1 |
750 |
|
29 |
0,57 |
26 |
0,42 |
15 |
0 |
750 |
|
30 |
0,58 |
27 |
0,43 |
16 |
2 |
750 |
|
31 |
0,59 |
27 |
0,45 |
17 |
2 |
750 |
|
32 |
0,55 |
28 |
0,48 |
14 |
1 |
750 |
|
33 |
0,53 |
29 |
0,49 |
15 |
2 |
750 |
|
34 |
0,55 |
26 |
0,50 |
15 |
1 |
743 |
|
35 |
0,54 |
25 |
0,43 |
14 |
1 |
750 |
|
36 |
0,55 |
24 |
0,47 |
17 |
0 |
750 |
|
37 |
0,56 |
26 |
0,56 |
15 |
3 |
750 |
|
38 |
0,57 |
28 |
0,58 |
14 |
4 |
750 |
|
39 |
0,58 |
27 |
0,59 |
14 |
2 |
750 |
|
40 |
0,56 |
27 |
0,52 |
15 |
1,6 |
749 |
Используя
аппарат математической статистики, изучим количественные признаки генеральной
совокупности по каждому из значений показателей результатов испытаний. Для этого
в распоряжении имеются данные выборки объемом ![]() (табл.
2).
(табл.
2).
Первый этап методики анализа контроля качества состоит в нахождении несмещенных оценок показателей, таких как выборочное среднее и исправленное среднее квадратическое отклонение (сопротивление теплопередачи, звукоизоляция, светопропускание, воздухопроницаемость, отклонение габаритных размеров, прочность угловых соединений), которые определялись по формулам:
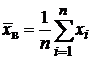 ,
, 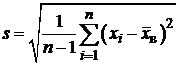 .
(1)
.
(1)
Данные
оценки позволяют определить для каждого показателя, подвергнутого анализу, доверительные
интервалы для математического ожидания ![]() при
неизвестном среднем квадратическом отклонении:
при
неизвестном среднем квадратическом отклонении:
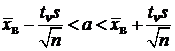 ,
,
где
число ![]() определяется по таблице
приложения 3 по заданному объему выборки
определяется по таблице
приложения 3 по заданному объему выборки ![]() и
надежности
и
надежности ![]() [1, с. 464]. Здесь от
случайной величины каждого из исследуемых показателей не требуется
распределения по нормальному закону [1, с. 214–219, 365]. Полученные значения после
первого этапа контроля представлены в табл. 3.
[1, с. 464]. Здесь от
случайной величины каждого из исследуемых показателей не требуется
распределения по нормальному закону [1, с. 214–219, 365]. Полученные значения после
первого этапа контроля представлены в табл. 3.
Таблица 3
Несмещенные оценки
|
Оценки |
Сопротивление теплопередаче, м² ·°С/Вт |
Звукоизоляция,
|
Светопропускание |
Воздухопроницаемость, м³/(ч·м²) |
Отклонение |
Прочность угловых |
|
Выборочное среднее |
0,55975 |
26,825 |
0,43975 |
15,625 |
1,44 |
748,125 |
|
Исправленное среднее
квадратическое отклонение |
0,016716 |
1,483024 |
0,080718 |
1,274755 |
0,982096 |
4,409707 |
|
Доверительный интервал: – левая граница – правая граница |
0,552593 0,566907 |
26,19001 27,45999 |
0,40519 0,47431 |
15,07919 16,17081 |
1,019494 1,860506 |
746,2369 750,0131 |
Примечание. В данной таблице границы доверительных
интервалов рассчитаны для надежности ![]() , т.е.
, т.е. ![]() .
.
Второй этап методики анализа контроля качества заключается в сравнении нормативных значений с доверительными границами (табл. 1 и 3). Здесь требуется выявить все показатели, доверительные интервалы которых не укладываются в требования нормативных документов. Назовем такие показатели ненадежными. В нашем случае ненадежным оказался единственный показатель, такой как прочность угловых соединений.
Далее
значения всех ненадежных показателей требуется исследовать на связь с другими
показателями, участвующими в анализе. Для этого достаточно определить выборочный
коэффициент корреляции ![]() для каждой пары,
содержащей обязательно ненадежный показатель. В табл. 4 представлены значения
выборочных коэффициентов корреляции.
для каждой пары,
содержащей обязательно ненадежный показатель. В табл. 4 представлены значения
выборочных коэффициентов корреляции.
Таблица 4
Значения выборочных коэффициентов корреляции
|
Ненадежный показатель |
Надежный показатель |
|
|
Прочность угловых соединений |
Сопротивление теплопередаче |
|
|
Прочность угловых соединений |
Звукоизоляция |
|
|
Прочность угловых соединений |
Светопропускание |
|
|
Прочность угловых соединений |
Воздухопроницаемость |
|
|
Прочность угловых соединений |
Отклонение габаритных размеров |
|
Конечно,
поскольку выборка отобрана случайно, то еще нельзя заключить, что коэффициент
корреляции генеральной совокупности также отличен от нуля. Следовательно, возникает
необходимость при заданном уровне значимости ![]() проверить
нулевую гипотезу
проверить
нулевую гипотезу ![]() о равенстве нулю
генерального коэффициента корреляции при конкурирующей гипотезе
о равенстве нулю
генерального коэффициента корреляции при конкурирующей гипотезе ![]() . Если нулевая гипотеза отвергается, то
это означает, что выборочный коэффициент значимо отличается от нуля, а
совокупность показателей связаны линейной зависимостью [1, с. 327].
. Если нулевая гипотеза отвергается, то
это означает, что выборочный коэффициент значимо отличается от нуля, а
совокупность показателей связаны линейной зависимостью [1, с. 327].
Для
этого были определены критические точки ![]() и
рассчитаны значения критерия
и
рассчитаны значения критерия ![]() для каждого
выборочного коэффициента корреляции:
для каждого
выборочного коэффициента корреляции:
![]() ,
,
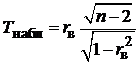
где
![]() – уровень значимости. В итоге были
получены следующие результаты:
– уровень значимости. В итоге были
получены следующие результаты:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Как
видно, ![]() , что свидетельствует о
линейной зависимости прочности угловых соединений и сопротивления теплопередачи.
, что свидетельствует о
линейной зависимости прочности угловых соединений и сопротивления теплопередачи.
Выводы
Таким образом, особому контролю должны подлежать все коррелируемые (зависимые) показатели, как прочность угловых соединений (особо важно) и сопротивления теплопередачи.
В случае если связи между исследуемыми показателями не существенны, меры по особому контролю или же устранению брака в готовой продукции нужно производить только по ненадежному показателю.
Рецензенты:Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и ТСП», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Данилов А.М., д.т.н., профессор кафедры математики и математического моделирования, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.



