Транспортировка важная область жизнедеятельности человека. Перевозка людей и грузов (как пищевых, так и промышленных) — это неотъемлемая часть жизни современного человека. Так расходы на транспортировку различных видов грузов составляют в Великобритании -15%, во Франции — 9%, в Дании - 15% от общих национальных расходов. Необходимость решения таких транспортных задач, с минимизацией издержек на перевозку, определяется большим экономическим эффектом при нахождении лучшего решения, т.к. это явно увеличивает прибыль предприятия. Таким образом, решение транспортных задач большой размерности является актуальной задачей. [4]
Транспортную задачу размерности 20х10 можно решать в среде MS Excel, а большей размерности уже в пакете MathCAD.
Алгоритм решения транспортной задачи большой размерности
Постановка задачи
Транспортная задача является специальным типом задач линейного программирования и формулируется следующим образом. Имеется m пунктов отправления (или пунктов производства) Аi,..., Аm, в которых сосредоточены запасы о днородных продуктов в количестве a1, ..., аm единиц. Имеется n пунктов назначения (или пунктов потребления) В1, ..., Вm, потребность которых в указанных продуктах составляет b1,..., bn единиц. Известны также транспортные расходы cij, связанные с перевозкой единицы продукта из пункта Ai в пункт Вj, i 1, ..., m; j 1, ..., n. Пусть Xij - количество единиц продукта, поставляемого из пункта Аi в пункт Вj. Предположим, что
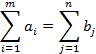
т. е. общий объем производства равен общему объему потребления. Приведенная формулировка транспортной задачи называется замкнутой транспортной моделью. Формализуем эту задачу.
Математическая постановка этой задачи имеет вид:
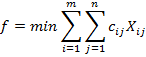
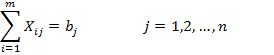
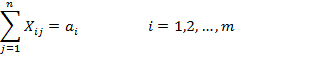
![]()
Объемы перевозок - неотрицательные числа, так как перевозки из пунктов потребления в пункты производства исключены.
Решение транспортной задачи является оптимальным планом перевозок (поставок) продукции.
Таким образом, транспортная задача сводится к минимизации суммарных затрат при выполнении условий полного удовлетворения спроса и равенства вывозимого количества продукта запасам его в пунктах отправления.[2]
Алгоритм решения транспортной задачи с помощью пакета MathCAD
1. Зададим значение m (количество производителей на единицу меньше).
2. Зададим значение n (количество потребителей на единицу меньше).
3. Зададим диапазон изменения для i (от 0 до m) иj (от 0 до n).
4. Введем вектор ![]() и вектор
и вектор ![]()
5. Введем массив запасов aи массив потребностей b
6. Теперь сформируем массив транспортных расходов. Для этого разобьем нашу таблицу на несколько массивов. Их можно разбивать по горизонтали, по вертикали и даже по вертикали и по горизонтали. Введем эти массивы.
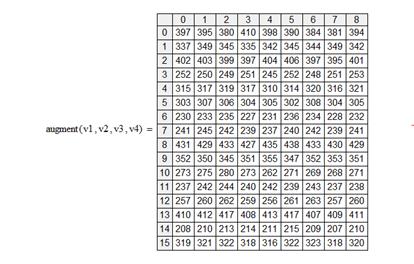
7. С помощью специальной функции augment (…..),в которой аргументами являются эти массивы, записывающиеся через запятую, соберем наш массив транспортных расходов.
8. Присвоим значение этой функции массиву с.
9. Результат выведем на экран.
10. Запишем формулу суммарных затрат и начальному приближению присвоим 0.
11. Вводим необходимые условия: условие полного удовлетворения спроса, условие равенства вывозимого количества продукта запасам его в пунктах отправления и условие неотрицательности.
12. Массиву Х присвоим функцию Minimize (f,x) для минимизации наших расходов.
13. Выведем этот массив.
14. Найдем суммарные затраты f(x). [1]
Пример
Рассмотрим алгоритм решения транспортной задачи для 16 производителей и 23 потребителей. [3,5]
m:= 15
n:= 22
i:= 0..15
j:= 0..22
![]()
![]()
Рис. 1. Ввод массива запасов и массива потребностей

Рис. 2. Разбиение таблицы на несколько массивов
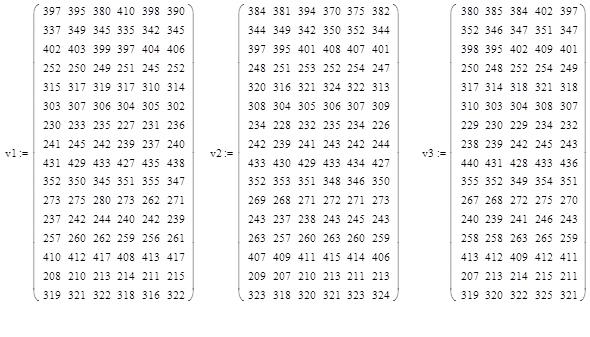
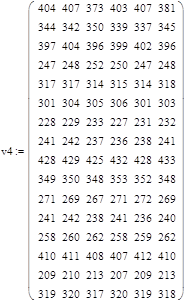
Рис. 3. Полученный результат после объединения массивов
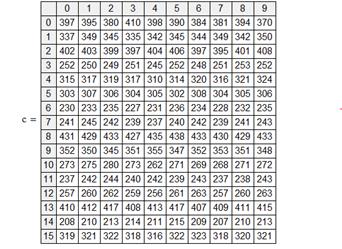
c:= augment(v1,v2,v3,v4)
Рис. 4. Вывод массива с:
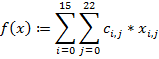
![]()
Given
![]()
![]()
![]()
x:=Minimize (f,x)
Рис. 5. Вывод массива x:
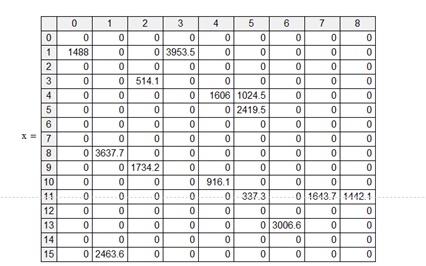
14). f(x) = 19554634
Заключение
Так как транспортная задача имеет экономический подтекст, то она является актуальной для различного масштаба производственных и торговых предприятий. Разработан алгоритм для нахождения опорного плана транспортной задачи, который можно применять для решения транспортных задач, представленных в матричном виде порядка больше 20x10. Приведенный пример, позволяет сделать вывод, о том что данный алгоритм возможно использовать для эффективного нахождения опорного плана транспортной задачи.
Рецензенты:
Первадчук В.П., д.т.н., профессор, зав. кафедрой «Прикладная математика» ПНИПУ, г. Пермь.
Цаплин А.И., д.т.н., профессор, ПНИПУ, г. Пермь.



