Одной из моделей неопределенности является сочетание в ней нечеткости и случайности. Это приводит к появлению нечетких случайных переменных. Наиболее часто встречаются гибридные данные, когда вектор условной плотности экспериментальных данных имеет нечеткие параметры. Например, одномерная нечеткая случайная переменная 
имеет нормальную плотность с нечетким математическим ожиданием 
и нечетким средним квадратическим отклонением
или в символической форме
, где N- символ «нормальности» 
,- заданные функции принадлежностей.
Актуальной задачей обработки гибридных данных является сглаживание (фильтрации) случайной составляющей и нахождении результирующей функции принадлежностей. Для решения этой задачи будем использовать метод наименьших квадратов (МНК).
Постановка Задачи
Имеем вектор 
«гибридных» данных, « H » - индекс нечеткости. Необходимо сгладить их методом наименьших квадратов (МНК). Предполагается, что выполнены следующие условия. Данные 
Связаны линейной моделью:
где
-нечеткая случайная переменная с симметричной плотностью и параметрами:
-единичная матрица,
- заданная четкая константа; нечеткость 
задается с помощью функции принадлежностей 
треугольного типа с параметрами
- заданные базисные функции модели;
- неизвестные параметры модели, подлежащие определению по "m" измерениям: 
, которые получены в моменты времени 
- число измерений "n" больше числа "m" неизвестных параметров модели.
Метод Решения
В соответствии с МНК вектор оценок 
находится из условия
где 
- прямоугольная матрица;
– вектор параметров модели, подлежащий определению. Для минимизации квадратичной формы 
использует преобразования, связанные с алгеброй матриц, тогда получим нечеткую линейную систему (НЛС) относительно вектора Х
где 
- квадратная матрица с 
из элементов скалярных произведений заданных базисных функций 
и
в
. Очевидно, что элементы матрицы являются четкими переменными. Вектор 
является вектором нечетких переменных.
Полученная НЛС решается в соответствии с методикой изложенной в [2]. В результате находится вектор нечетких оценок 
, который может быть «сильным» или «слабым». Здесь под "сильным"
подразумевается вектор, для которого все нечеткие компоненты 
:
удовлетворяют условиям:
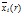-монотонно убывающая функция ; 
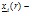Монотонно возрастающая функция;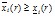 
Если хотя бы для одной из компонент 
нарушается одно из условий (i)
(iii), то после соответствующей замены переменных, при которой уже выполняются упомянутые соотношения, тогда нечеткий вектор 
принято называть "слабым"[1].
Нечеткая оценка модели будет равна:
Как и ранее она может быть либо "сильной", либо "слабой". Если все 
являются «сильными», то 
- сильная модель. Если хотя бы одна из
является слабой, то 
- «слабая» модель.
Пример 1.
Имеем модель:
где 
- базисная функция модели; 
- нечеткая случайная переменная, распределенная по равномерному закону на промежутке
с функцией принадлежности
типа равнобедренного треугольника с параметрами 
-дисперсия равномерного распределения:
, тогда:
или в эквивалентной уровневой форме:
Пусть в результате генерации одной из реализаций равномерного закона на 
было получено: 
тогда нечеткие случайные переменные будут соответственно равны:
В итоге получим вектор 
«гибридных» данных
,
где 
Далее для "m=4"измерений имеем:
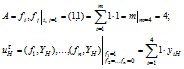
В результате получим НЛС:
, поэтому НЛС невырождена. Расширенная НЛС будет иметь вид:
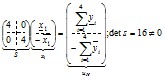
Поэтому
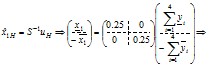
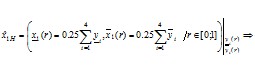
нечеткая «сильная» оценка, т.е. относительно 
,
выполнены условия (i)
(iii) Нечеткая «сильная» оценка модели равна:
Задавая 
как некую функцию векторного параметра "α"можно получить «слабую» оценку
и
.
Пример 2.
Имеем модель: 
Здесь 
- базисные функции 
. Получены нечеткие случайные данные (m=3):
Вычисления дают:
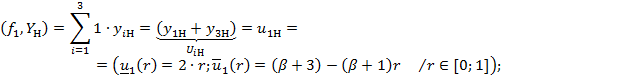
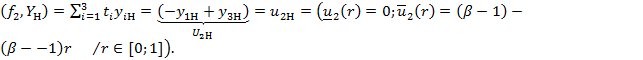
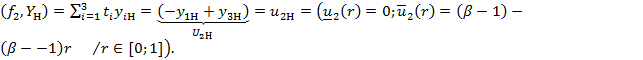
В результате получим:
.
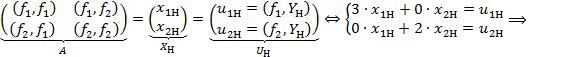
Оценка 
является «сильной», если компоненты 
удовлетворяют условиям:
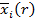
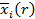- монотонно убывающая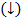 
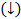
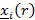
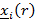- монотонно возрастающая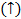 
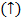
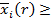
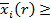
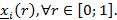
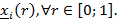
Для
имеем:
;
поэтому при 
, т.е справедливо (iii). Это означает, что
является «сильной» оценкой при 
.
Аналогичные вычисления для 
дают, что при 
оценка 
является «сильной», а при 
она является «слабой». Это означает, что в зависимости от величины параметра "
" нечеткая оценка модели 
может быть либо «сильной», либо «слабой».
ВЫВОДЫ
- Разработана методика решения нечеткой линейной системы, которая возникает при сглаживании «гибридных» данных по методу наименьших квадратов.
- Моделируются «гибридные» данные для простейшей нечеткой линейной модели и показано, что она является «сильной» моделью.
- Указано направление получения «слабой» модели нечеткого случайного процесса.
Рецензенты:
Девеев А.И., д.т.н., профессор, зав. сектором вычислительного Центра Российской Академии наук (ВЦ РАН) им. А.А. Дородницына, г. Москва.
Воронов Е.М., д.т.н., профессор, государственный технический университет им. Н.Э. Баумана, г. Москва.