Если на тело массы m , находящегося на гладкой горизонтальной поверхности, действует
постоянная сила F , направленная под некоторым углом α к горизонту и при этом тело перемещается на некоторое расстояние S , то говорят, что сила F совершила работу A. Величину работы определяют по формуле [1,2,3]:
A = F × S cosα (1)
Однако в природе идеально гладких поверхностей не бывает, и на поверхности контакта двух тел всегда возникают силы трения. Вот как об этом пишется в учебнике [1, Стр. 200]: «Работа силы трения покоя равна нулю, поскольку перемещение отсутствует. При скольжении твердых поверхностей сила трения направлена против перемещения. Ее работа отрицательна. Вследствие этого кинетическая энергия трущихся тел превращается во внутреннюю - трущиеся поверхности нагреваются».
Автором данной статьи было просмотрено множество школьных и вузовских учебников и задачников, но работа против сил трения рассматривалась только применительно к равномерному движению:
АТР = FТР×S = μNS (2)
где μ - коэффициент трения скольжения.
Только в учебнике О.Д. Хвольсона [3, стр. 92] рассмотрен случай УСКОРЕННОГО ДВИЖЕНИЯ при наличии сил трения: «Итак, следует отличать два случая производства работы: в первом сущность работы заключается в преодолевании внешнего сопротивления движению, которое совершается без увеличения скорости движения тела; во втором - работа обнаруживается увеличением скорости движения, к которому внешний мир относится индифферентно.
На деле мы обыкновенно имеем СОЕДИНЕНИЕ ОБОИХ СЛУЧАЕВ: сила f преодолевает какие-либо сопротивления и в то же время меняет скорость движения тела.
Положим, что f' не равно f , а именно, что f'< f . В таком случае на тело действует сила
f - f', работа ρ которой вызывает увеличение скорости тела. Мы имеем ρ =(f - f')S ,
откуда
fS = f'S + ρ (*)
Работа r = fS состоит из двух частей: f 'S тратится на преодолевание внешнего сопротивления, ρ на увеличение скорости тела».
Представим это в современной интерпретации (рис. 1). На тело массы m действует сила тяги FT, которая больше силы трения FTP = μN = μmg. Работу силы тяги в соответствии с формулой (*) можно записать так
A=FT S =FTPS +FaS = ATP + Aa (3)
где Fa =FT - FTP - сила, вызывающая ускоренное движение тела в соответствии со II законом Ньютона: Fa = ma . Работа силы трения отрицательна, но здесь и далее мы будем использовать силу трения и работу трения по модулю. Для дальнейших рассуждений необходим численный анализ. Примем следующие данные: m =10 кг; g =10 м/с2; FT =100 Н; μ = 0,5; t =10 с. Проводим следующие вычисления: FTP = μmg = 50 Н; Fa = 50 Н; a=Fa /m=5 м/с2; V = at = 50 м/с; K = mV2 /2 =12,5 кДж; S = at2 /2 = 250 м; Aa = FaS =12,5 кДж; ATP =FTP S=12,5 kДж. Таким образом суммарная работа A = ATP + Aa =12,5 +12,5 = 25 кДж
А теперь рассчитаем работу силы тяги FT для случая, когда трение отсутствует ( μ =0 ).
Проводя аналогичные вычисления, получаем: a =10 м/с2; V =100м/с; K = 50 кДж; S = 500 м; A = 50 кДж. В последнем случае за те же 10 с мы получили работу в два раза больше. Могут возразить, что и путь в два раза больше. Однако, что бы ни говорили, получается парадоксальная ситуация: мощности, развиваемой одной и той же силой, отличаются в два раза, хотя импульсы сил одинаковы I =FTt =1 кН•с. Как писал М.В. Ломоносов еще в 1748 г.: «...но все изменения, совершающиеся в природе, происходят таким образом, что сколько к чему прибавилось столько же отнимется у другого...». Поэтому попробуем получить другое выражение для определения работы.
Запишем II закон Ньютона в дифференциальной форме:
F• dt = d(mV ) (4)
и рассмотрим задачу о разгоне первоначально неподвижного тела (трение отсутствует). Интегрируя (4), получим: F ×t = mV . Возведя в квадрат и разделив на 2m обе части равенства, получим:
F2t2 / 2m = mV 2 / 2 A= K (5)
Таким образом, получили другое выражение для вычисления работы
A = F2t2 / 2m = I2 / 2m (6)
где I = F × t - импульс силы. Это выражение не связано с путем S, пройденным телом за время t, т.е. оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным, хотя, как утверждают во всех курсах физики, в этом случае никакой работы не совершается.
Переходя к нашей задаче об ускоренном движении с трением, запишем сумму импульсов сил: IT = Ia + ITP, где IT = FTt; I a = F at ; ITP = FTPt. Возведя в квадрат сумму импульсов, получим:
FT2 t2 = Fa 2 t2 + 2Fa FTPt2 + FTP2 t 2
Разделив все члены равенства на 2m , получим:
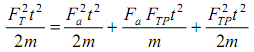 (7)
(7)
или A= Aa + AУТ + ATP
где Aa=F a2t 2 / 2m- работа, затрачиваемая ускорение; ATP = FTP 2 t 2 /2m - работа, затрачиваемая на преодоление силы трения при равномерном движении, а AУT =FaFTPt2/m- работа, затрачиваемая на преодоление силы трения при ускоренном движении. Численный расчет дает следующий результат:
A = Aa + AУт + ATP = 12,5 + 25 +12,5 = 50 кДж,
т.е. мы получили ту же самую величину работы, которую совершает сила FT при отсутствии трения.
Рассмотрим более общий случай движения тела с трением, когда на тело действует сила F, направленная под углом α к горизонту (рис. 2). Теперь сила тяги FT = F cos α, а силу FЛ=F sin α - назовем силой левитации, она уменьшает силу тяжести P = mg, а в случае FЛ = mg тело не будет оказывать давления на опору, будет находиться в квазиневесомом состоянии (состоянии левитации). Сила трения FTP = μ N = μ(P - FЛ). Силу тяги можно записать в виде FT=Fa+FTP, а из прямоугольного треугольника (рис. 2) получим: F2 =FТ2 +FЛ2. Умножая последнее соотношение на t2 , получим баланс импульсов сил, а разделив на 2m, получим баланс энергий (работ):
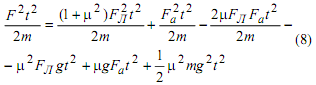
Приведем численный расчет для силы F = 100 Н и α = 30o при тех же условиях (m = 10 кг; μ = 0,5; t = 10 с). Работа силы F будет равна A = F2t2 /2m = 50 , а формула (8) дает следующий результат (с точностью до третьего знака после запятой):
50=15,625+18,974-15,4-12,5+30,8+12,5 кДж.
Как показывают расчеты, сила F = 100 Н, действуя на тело массы m = 10 кг под любым углом α за 10 с совершает одну и ту же работу 50 кДж.
Последний член в формуле (8) представляет собой работу силы трения при равномерном движении тела по горизонтальной поверхности со скоростью V
![]()
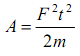
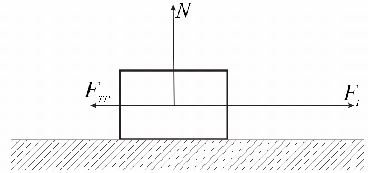
Рис.1
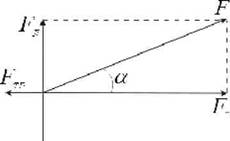
Рис.2
СПИСОК ЛИТЕРАТУРЫ
- Матвеев А.Н. механика и теория относительности. Учеб.пособие для физ.спец.вузов. -М.: Высш.шк., 1986.
- Стрелков СП. Механика. Общий курс физики. Т. 1. - М.: ГИТТЛ, 1956.
- Хвольсон О.Д. Курс физики. Т. 1. РСФСР Госуд.Изд-во, Берлин, 1923.



