Введение

В настоящий момент наблюдается значительный интерес к исследованию течений в пористых средах, сопровождающихся фазовыми переходами. Это обусловлено необходимостью теоретического изучения большого круга вопросов, возникающих, например, при решении вопросов добычи углеводородного сырья [2, 3]. В частности, многие процессы в нефтегазовой отрасли сопровождаются образованием газогидратов. В настоящий момент гидратообразование носит чаще негативный характер, вследствие аварийных остановок оборудования из-за «склероза». Однако процессы гидратообразования могут иметь и положительный аспект, например, могут быть использованы для увеличения емкости подземных резервуаров для хранения газа [4, 5, 6]. Данная возможность обусловлена резким увеличением содержания газа в газогидратном состоянии [9, 10].

Постановка задачи и основные уравнения

Рассмотрим прямолинейно-параллельную задачу об образовании газогидрата в полубесконечном пористом пласте. Пусть пористый пласт в начальный момент времени насыщен газом и водой, давление и температура которых в исходном состоянии соответствуют термодинамическим условиям существования гетерегенной смеси газа и воды в свободном состоянии, т.е. , где – равновесное давление, соответствующее исходной температуре . Положим, что через границу пласта нагнетается газ, одноименный исходному, причем его давление и температура Te соответствуют термодинамическим условиям образования газогидрата и поддерживаются на этой границе постоянными. При постановке задачи будем полагать, что в результате инжекции газа от границы вглубь пористой среды начинает распространяться фронтальная граница образования гидрата, разделяющая пласт на две области. В ближней области, находящейся вблизи границы пласта, вода полностью перешла в газогидратное состояние, вследствие чего поры насыщены только газом и газогидратом, а в дальней области поры насыщены водой и газом.

Система основных уравнений, описывающая процессы фильтрации и теплопереноса, сопровождающиеся образованием газогидрата в пористой среде представляет собой законы сохранения масс и энергии, закон Дарси и уравнение состояния для газа [8]:

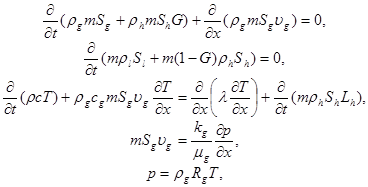(1)

где m – пористость; G – массовая концентрация газа в гидрате; и (j = h, l, g) – истинные плотности и насыщенности пор j – ой фазы; , , и – соответственно скорость, проницаемость, удельная теплоемкость и динамическая вязкость газа; p – давление; T – температура; – удельная теплота гидратообразования; и – удельная объемная теплоемкость и коэффициент теплопроводности системы; индексы h, l и g относятся к параметрам гидрата, воды и газа соответственно.

На границе между областями для температуры и давления выполняется условие фазового равновесия [7]:

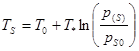, (2)

где – исходная температура системы, – равновесное давление, соответствующее исходной температуре, – эмпирический параметр.

Будем полагать, что в начальный момент давление и температура во всех точках пласта одинаковы: .

Условия на границе пласта запишем, полагая, что газ нагнетается при постоянных значениях давления и температуры: .

Cистему уравнений (1)после преобразований можно записать в виде:

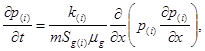(3)

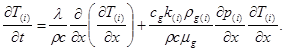(4)

Здесь параметры первой (ближней) и второй (дальней) областей снабжены нижними индексами в скобках i = 1, 2.

Система уравнений для нахождения координаты границы фазовых переходов и значений параметров на ней имеет вид:

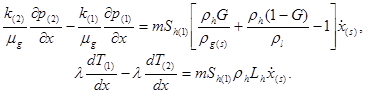(5)

Здесь – скорость движения границы фазового перехода (нижний индекс s в скобках относится к параметрам на границе гидратообразования)

Автомодельное решение

Сформулированная таким образом задача имеет автомодельное решение. Введем автомодельную переменную , где – коэффициент температуропроводности.

Тогда уравнение пьезопроводности (3), после применения метода линеаризации Лейбензона [5], запишется следующим образом:

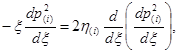(6)

где

Уравнение температуропроводности (4) в автомодельных переменных можно представить в виде:

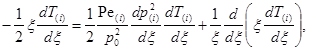(7)

где – число Пекле.

На основе соотношений (5) запишем систему уравнений для нахождения автомодельной координаты границы фазовых переходов и значений параметров на ней:

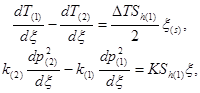(8)

где

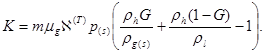
Проинтегрировав уравнения (6) и (7) можно получить следующие аналитические решения, описывающие распределения давления и температуры в пласте:

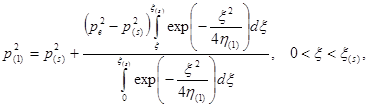(9)

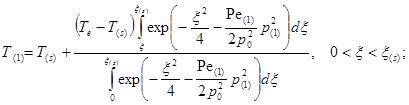
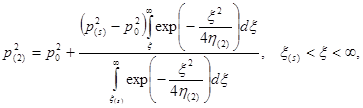(10)

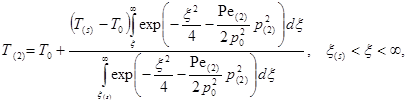
где .

Система граничных условий (8) после подстановки решений (9) и (10) примет вид:

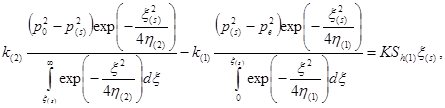(11)

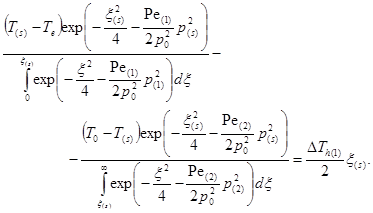(12)

Записанная система уравнений может быть решена следующим образом. Выражая из уравнения (11) величину и подставляя ее в соотношение (12), получаем с учетом условия (2) трансцендентное уравнение с одной неизвестной Решая данное уравнение (например, методом половинного деления), определяем величину , а затем находим распределение давления и температуры в первой и второй области, в том числе и значения данных параметров на границе между областями.

Результаты расчетов

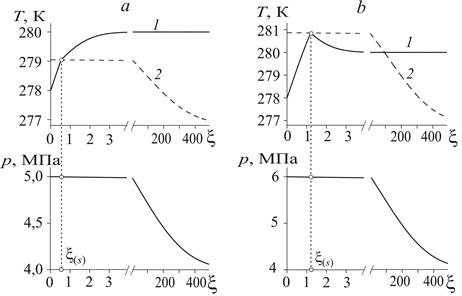
Рис. 1. Распределения температуры пласта (1), равновесной температуры (2) и давления.

a – непротиворечивый случай: pe = 5 МПа, Te = 278 К;

b – случай «переохлаждения» воды за фронтом: pe = 6 МПа, Te = 278 К.

На рис. 1a представлены распределения температуры и давления при нагнетании метана под давлением =5 МПа с температурой =278 К в пласт с начальным давлением =4 МПа и исходной водонасыщенностью = 0,2. Для остальных параметров, характеризующих систему, приняты следующие значения: Штриховая линия 2 показывает равновесную температуру, соответствующую полученному распределению давления. Из данного рисунка видно, что температура пласта перед фронтом гидратообразования ниже равновесной температуры, а за фронтом – выше этой температуры. Следовательно, в этом случае решение с фронтальной поверхностью образования гидрата является непротиворечивым.

На рис. 1b приведены распределения температуры и давления при нагнетании метана под давлением МПа с температурой . В соответствии с рисунком температура пласта за фронтом гидратообразования опускается ниже равновесной температуры (штриховая линия 2), что соответствует переохлаждению воды в этой области. Таким образом, при данном давлении нагнетания газа модель с фронтальной поверхностью образования гидрата не позволяет построить физически непротиворечивое решение. В этом случае для построения термодинамически непротиворечивого решения необходимо рассматривать объемную область образования газогидрата.

Для определения критического значения давления нагнетания газа, при превышении которого фронтальная поверхность переходит в объемную область образования гидрата, были проведены вычислительные эксперименты в широком диапазоне параметров. В результате было установлено, что фронтальный режим реализуется в низкопроницаемых пористых средах, а также в высокотемпературных пластах с низким пластовым давлением.

Выводы

Разработана математическая модель инжекции холодного газа в пористую среду, сопровождающаяся гидратообразованием. Установлено, что образование газогидрата может происходить как на фронтальной поверхности, так и в протяженной области.

Работа поддержана грантом Российского фонда фундаментальных исследований.

Рецензенты:

Мустафина С.А., д.ф.-м.н., профессор, декан физико-математического факультета Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак.

Михайлов П.Н., д.ф.-м.н., профессор, заведующий кафедрой «Алгебры, геометрии и методики обучения математике» Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак.