Введение
Конические оболочечные конструкции находят большое применение в различных областях техники и могут подвергаться длительным механическим нагрузкам. При длительном нагружении в материале конструкции могут развиться деформации ползучести [1; 4].
Поэтому расчеты прочности и устойчивости подкрепленных конических оболочек должны вестись с учетом возможности развития деформации ползучести.
Одной из первых работ по устойчивости конических оболочек была работа Х.М. Муштари (Муштари Х.М. Об устойчивости тонкостенных конических оболочек круглого сечения при кручении парами // Сборник научных трудов КАИ. – Казань : Издательство Казанского авиационного института, 1935. – С. 39–40). Кроме этого, следует отметить работу Муштари Х.М. и Саченкова А.В. (Муштари Х.М., Саченков А.В. Об устойчивости цилиндрических и конических оболочек круглого сечения при совместном действии осевого сжатия и внешнего нормального давления // Прикладная математика и механика. - 1954. - Т. XVIII, № 6. - С. 667–674).
Следует отметить также работы Н.А. Алумяэ, Э.Н. Григолюка, Х.М. Муштари, А.В. Саченкова, И.Н. Преображенского, Н.В Валишвили и др. В работе Валишвили Н.В. [2] исследуется устойчивость конических оболочек на основе осесимметричной теории. В работе Преображенского И.Н., Грищак В.З. [7] для исследования устойчивости конических оболочек используется упрощённая теория и получены оценки критической нагрузки.
Однако все исследования проводились в линейно-упругой постановке.
Цель исследования
Разработка математической модели деформирования конических оболочек при учете ползучести материала.
Материал и методы исследования
Схематичное изображение и принятая локальная система координат панели конической оболочки показаны на рисунке 1.
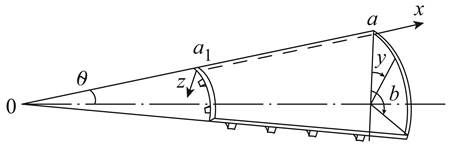
Рис. 1. Панель конической оболочки.
Для учета ползучести материала будем использовать линейную теорию наследственной ползучести.
Физические соотношения (связь напряжений и деформаций) для упругого изотропного материала оболочки будут иметь вид
![]()
![]() (1)
(1)
![]()
Таким образом, физические соотношения для изотропного материала принимают вид
![]()
![]() (2)
(2)
![]()
![]()
Физические соотношения при учете ползучести материала можно представить в виде
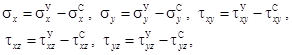
где ![]() имеют вид (2), а напряжения, отражающие развитие деформаций ползучести, согласно линейной теории наследственности будут иметь вид
имеют вид (2), а напряжения, отражающие развитие деформаций ползучести, согласно линейной теории наследственности будут иметь вид
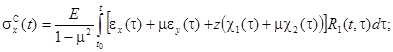
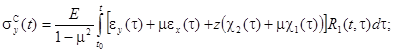
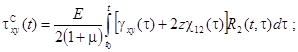 (3)
(3)
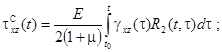
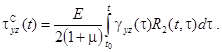
Если для решения задачи ползучести применяется итерационный процесс по координате ![]() и отрезок
и отрезок ![]() разбит на части точками
разбит на части точками ![]() с шагом
с шагом ![]() сутки, то приближенно можно принять
сутки, то приближенно можно принять
![]()
![]()
![]()
![]()
![]()
где ![]() ,
, ![]() .
.
Например, для оргстекла
![]()
и тогда
![]()
Математическая модель деформирования конических оболочек представляет собой функционал полной энергии деформации оболочки, который при учете ползучести материала имеет вид
![]() (4)
(4)
Здесь
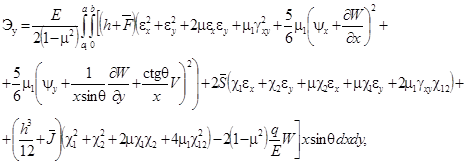 (5)
(5)
где ![]() .
.
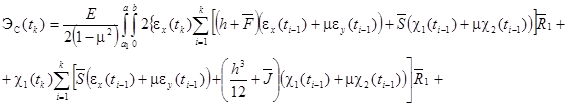
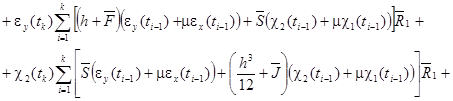
![]()
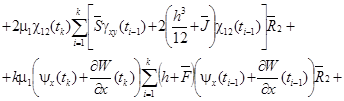
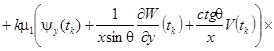
![]() (6)
(6)
Функционал (4) с учетом (5), (6) вместе с краевыми условиями представляет собой математическую модель деформирования конической оболочки при учете ползучести материала, в которой учитывается геометрическая нелинейность, дискретное введение ребер с учетом их сдвиговой и крутильной жесткости, поперечных сдвигов.
В выражениях (5), (6) ![]() – деформации в координатной поверхности оболочки, за которую принята срединная поверхность обшивки [6], для конической оболочки они принимают вид
– деформации в координатной поверхности оболочки, за которую принята срединная поверхность обшивки [6], для конической оболочки они принимают вид
![]()
![]()
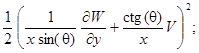
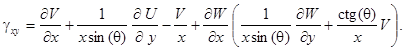
Здесь ![]() – перемещения точек координатной поверхности вдоль осей
– перемещения точек координатной поверхности вдоль осей ![]() ;
; ![]() – функции, характеризующие поперечные сдвиги в соответствующих плоскостях;
– функции, характеризующие поперечные сдвиги в соответствующих плоскостях; ![]() – модуль Юнга и коэффициент Пуассона материала;
– модуль Юнга и коэффициент Пуассона материала; ![]() – составляющая поперечной нагрузки;
– составляющая поперечной нагрузки; ![]() – толщина оболочки;
– толщина оболочки; ![]() – предельные значения координат
– предельные значения координат ![]() ;
; ![]() – функции изменения кривизны и кручения [6]:
– функции изменения кривизны и кручения [6]:
![]()
![]()
Переменными ![]() обозначены функции, выражающие площадь поперечного или продольного сечения ребер, приходящуюся на единицу длины сечения, статический момент и момент инерции этого сечения:
обозначены функции, выражающие площадь поперечного или продольного сечения ребер, приходящуюся на единицу длины сечения, статический момент и момент инерции этого сечения:
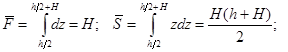
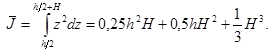
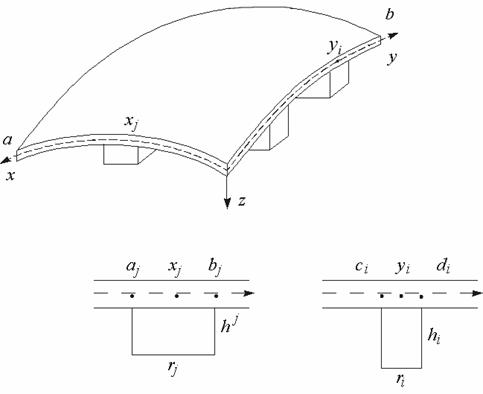
Рис. 2. Схема подкрепления оболочки ребрами жесткости.
Высота и расположение ребер задается функцией
![]()
![]()
где ![]() - высота ребер, параллельных осям
- высота ребер, параллельных осям ![]() и
и ![]() соответственно;
соответственно; ![]() ;
; ![]() ,
, ![]() - единичные столбчатые функции, равные единице в местах присоединения ребер и равные нулю вне таких мест. Контакт ребра и обшивки происходит по полосе.
- единичные столбчатые функции, равные единице в местах присоединения ребер и равные нулю вне таких мест. Контакт ребра и обшивки происходит по полосе.
В развернутом виде ![]() принимают вид [3]
принимают вид [3]
![]()
![]() ;
;
![]() ;
;
![]()
![]() ,
,
где, например,
![]()
![]()
Ребра, параллельные оси ![]() (j-е ребра), расположены при
(j-е ребра), расположены при ![]() , а ребра, параллельные оси
, а ребра, параллельные оси ![]() (i-е ребра), расположены при
(i-е ребра), расположены при ![]() . Причем
. Причем
![]()
Здесь ![]() .
.
Так как ![]() , то –
, то – ![]() константы. Чтобы i-е ребра были одной ширины при любом
константы. Чтобы i-е ребра были одной ширины при любом ![]()
![]()
Заключение
Таким образом, модель конической оболочки при учете ползучести материала, записанная в виде функционала полной энергии деформации оболочки, может быть исследована с использованием вариационного метода Ритца, т.е. для исследования устойчивости подкрепленных конических оболочек можно использовать методику, описанную в работе [5]. Для исследования ползучести материала используется итерационный процесс.
Рецензенты:
Ушаков А.И., д.т.н., профессор научно-производственного информационно-консультационного центра – плюс, г. Санкт-Петербург.
Максимов С.Е., д.т.н., профессор, генеральный директор научно-производственной компании «НТМТ», Ленинградская обл., г. Гатчина.



