Введение
Работоспособность технологического оборудования обеспечивается рядом параметров механизма привода, основными из которых являются кинематические параметры. Процесс модернизации и дальнейшего развития промышленного потенциала РФ выводит на первый план потребность формирования приводов технологического оборудования на базе механизмов, обладающих достаточно простой структурой, образованной минимально возможным числом подвижных звеньев и кинематических пар. Повышение эффективности технологического оборудования является актуальной задачей, решение которой возможно обеспечить посредством использования механизмов с замкнутой системой тел качения (ЗСТК), обладающих требуемыми передаточными отношениями и позволяющих реализовать сложное движение выходного звена при минимально возможном числе подвижных звеньев. Механизмы с ЗСТК обладают структурой, которая образована совокупностью двух колец с дорожками качения, сепаратора (водило) и тел качения с диаметрами равной или разной величины, которые могут обладать гладкими рабочими поверхностями (фрикционные) [1; 3-10] или поверхностями с выступами (зубчатые) [1]. Коллектив авторов проводит исследования геометрических и кинематических параметров исполнительных механизмов технологического оборудования, разработанного на базе механизмов с ЗСТК с диаметрами разной (эксцентриковые) [1-3; 8-10] или равной (соосные) [4-7] величины. В ходе исследований [1-10] установлено, что задача определения номинальных значений геометрических параметров механизмов с ЗСТК имеет решение только при двух направлениях ввода поправки, т.е. либо ![]() , либо
, либо ![]() .
.
Для механизмов с ЗСТК с диаметрами разной величины характерно наличие нескольких видов структурных схем механизмов (рис. 1).
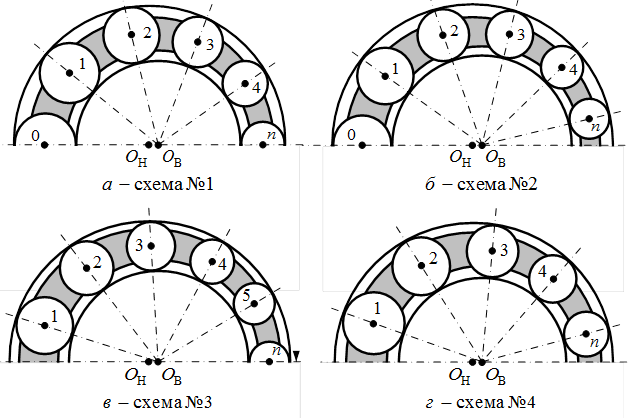
Рис. 1. Виды симметричных структурных схем механизмов с ЗСТК с диаметрами разной величины
Наличие сепаратора в структуре механизмов с ЗСТК (рис. 1) позволяет исключить контакт тел качения друг с другом, обеспечив между ними наличие зазора. Передача движения между звеньями в этом случае осуществляется посредством непосредственного контакта тел качения с дорожками качения обоих колец. Механизмы данного вида относятся к фрикционным эпициклическим механизмам, что указывает на наличие скольжения в зонах контакта их звеньев. Для обеспечения работоспособности механизмов с ЗСТК необходимо создать достаточное прижатие контактирующих поверхностей звеньев. Это невозможно без определения величин скоростей скольжения точек контакта тел качения с дорожками качения обоих колец, непосредственно оказывающих влияние на передаточное отношение.
Настоящее исследование проводится с целью разработки алгоритма определения скоростей скольжения точек контакта звеньев механизмов с ЗСТК с диаметрами разной величины для любого вида симметричной структурной схемы при ведущем наружном кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Полученные результаты позволят обеспечить работоспособность приводов технологического оборудования на базе механизмов с ЗСТК с диаметрами разной величины.
Методы исследования, применяемые в настоящей работе, основаны на принципах кинематического анализа эпициклических механизмов при использовании положений геометрии и тригонометрии.
В соответствии с вышеуказанной целью рассмотрим ход решения поставленной задачи на примере расчета величин скоростей скольжения точек контакта i-го тела качения с дорожками качения обоих колец механизма с ЗСТК с диаметрами разной величины при ведущем наружном кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Для этого составим расчетную модель (рис. 2) и примем следующие исходные условия и обозначения: ДКВ, ДКН – дорожки качения внутреннего и наружного колец; RВ, RН, ОВ и OН – радиусы и геометрические центры дорожек качения внутреннего и наружного колец; e – эксцентриситет; S – сепаратор (водило); с – зазор между телами качения; r0, r1, ri и 0, 1, i – радиусы и геометрические центры максимального, первого и i-го тел качения; 0H, 1H, i H и 0B, 1B, i B – точки контакта i-го тела качения с дорожками качения наружного и внутреннего колец; XВ OВ YВ – неподвижная система координат, жестко связанная с внутренним кольцом; XН OВ YН, Xi iВ Yi и XВi i YВi – подвижные системы координат, жестко связанные с наружным кольцом и i-м телом качения; jH – угловая координата наружного кольца в неподвижной системе координат XВ OВ YВ; ![]() и
и ![]() – угловые координаты точки i-го тела качения в подвижных системах координат Xi iВ Yi и XВi i YВi.
– угловые координаты точки i-го тела качения в подвижных системах координат Xi iВ Yi и XВi i YВi.
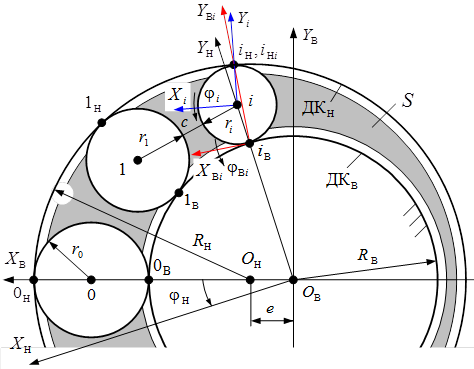
Рис. 2. Расчетная модель механизма с ЗСТК с диаметрами разной величины и зазором
Анализ расчетной модели механизма с ЗСТК (рис. 2) при рассматриваемых условиях показывает, что двойная точка контакта i-го тела качения с дорожкой качения наружного кольца образована совпадением точек ![]() и
и ![]() , расположенных на поверхностях обоих контактирующих звеньев, которые в статическом состоянии механизма совпадают. При движении звеньев точки
, расположенных на поверхностях обоих контактирующих звеньев, которые в статическом состоянии механизма совпадают. При движении звеньев точки ![]() и
и ![]() будут перемещаться с разными линейными скоростями. В этом случае положение точки
будут перемещаться с разными линейными скоростями. В этом случае положение точки ![]() , принадлежащей дорожке качения наружного кольца в подвижной системе координат XН OВ YН, определяется при помощи радиус-вектора
, принадлежащей дорожке качения наружного кольца в подвижной системе координат XН OВ YН, определяется при помощи радиус-вектора
![]() (1)
(1)
где ![]() – матрица поворота дорожки качения наружного кольца с угловой координатой
– матрица поворота дорожки качения наружного кольца с угловой координатой ![]() ;
; ![]() – радиус-вектор, определяющий положение точки
– радиус-вектор, определяющий положение точки ![]() , принадлежащей дорожке качения наружного кольца в неподвижной системе координат XВ OВ YВ.
, принадлежащей дорожке качения наружного кольца в неподвижной системе координат XВ OВ YВ.
Представим составляющие формулы (1) в виде
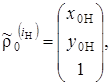 (2)
(2)
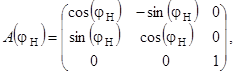 (3)
(3)
![]() (4)
(4)
здесь ![]() ,
, ![]() – координаты точки
– координаты точки ![]() , принадлежащей дорожке качения наружного кольца в системе координат YН OВ XН;
, принадлежащей дорожке качения наружного кольца в системе координат YН OВ XН; ![]() ,
, ![]() – матрицы перехода [8] координат дорожки качения наружного кольца в неподвижную систему координат XВ OВ YВ;
– матрицы перехода [8] координат дорожки качения наружного кольца в неподвижную систему координат XВ OВ YВ; ![]() – единичный вектор.
– единичный вектор.
Абсолютное движение точки ![]() , принадлежащей i-му телу качения, разложим на два составляющих движения (рис. 2). Первым является относительное вращательное движение вокруг оси, проходящей через его центр c угловой координатой
, принадлежащей i-му телу качения, разложим на два составляющих движения (рис. 2). Первым является относительное вращательное движение вокруг оси, проходящей через его центр c угловой координатой ![]() . Вторым является вращательное движение центра i-го тела качения вокруг оси, проходящей через мгновенный центр скоростей (точки
. Вторым является вращательное движение центра i-го тела качения вокруг оси, проходящей через мгновенный центр скоростей (точки ![]() ) с угловой координатой
) с угловой координатой ![]() . Тогда положение точки
. Тогда положение точки ![]() , принадлежащей i-му телу качения в подвижной системе координат XН OВ YН , определяется при помощи радиус-вектора
, принадлежащей i-му телу качения в подвижной системе координат XН OВ YН , определяется при помощи радиус-вектора
![]() (5)
(5)
где ![]() и
и ![]() – матрицы поворота i-го тела качения относительно точек
– матрицы поворота i-го тела качения относительно точек ![]() и
и ![]() ;
;
![]() – радиус-вектор, определяемый по равенству (4).
– радиус-вектор, определяемый по равенству (4).
Представим составляющие формулы (5) в виде
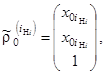 (6)
(6)
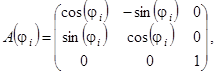 (7)
(7)
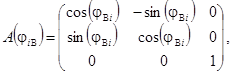 (8)
(8)
здесь ![]() ,
, ![]() – координаты точки
– координаты точки ![]() принадлежащей i-му телу качения в подвижной системе YН OВ XН.
принадлежащей i-му телу качения в подвижной системе YН OВ XН.
Подставив равенства (6)-(8) в выражение (5) и преобразовав, получим
![]() (9)
(9)
где
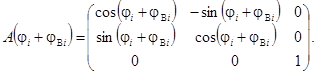 (10)
(10)
Абсолютное скольжение в зоне контакта i-го тела качения с дорожкой качения наружного кольца механизма с ЗСТК с диаметрами разной величины определим как
![]() (11)
(11)
Подставив в формулу (11) равенства (1) и (9) и продифференцировав по времени с учетом (2)-(4), (6)-(8) и (10), получим
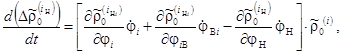 (12)
(12)
здесь
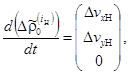 (13)
(13)
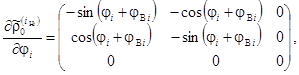 (14)
(14)
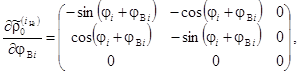 (15)
(15)
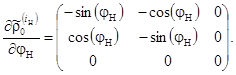 (16)
(16)
Подставив в формулу (12) равенства (13)-(16) и преобразовав, будем иметь
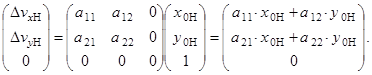 (17)
(17)
Приведем равенство (17) к параметрическому виду
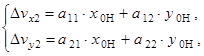 (18)
(18)
где
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
В результате решения системы (18) с учетом равенств (19)-(22) получим формулу для расчета скорости скольжения двойной точки контакта i-го тела качения с дорожкой качения наружного кольца механизма с ЗСТК с диаметрами разной величины
![]() (23)
(23)
Используя программный комплекс «Эксцентрик», зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ № 2012614197), выполняем расчет скоростей скольжения двойных точек контакта тел качения с дорожкой качения наружного кольца механизма с ЗСТК с диаметрами разной величины для всех видов симметричных структурных схем. Примем, что RН = 100 мм, RВ = 50 мм, е = 6 мм, с = 6 мм, угловая скорость наружного кольца wН = 50 с-1. По полученным результатам выполняем синтез диаграммы скоростей скольжения (рис. 3).
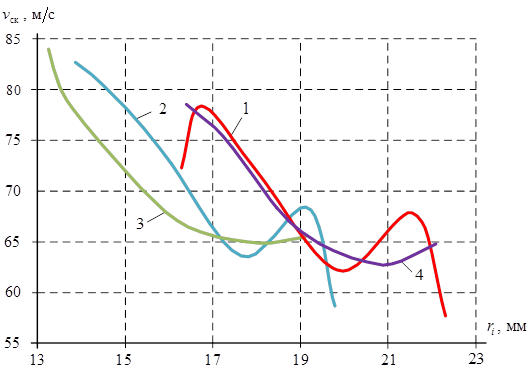
Рис. 3. Диаграмма скоростей скольжения точек контакта тел качения с дорожкой качения наружного кольца механизма с ЗСТК с диаметрами разной величины
Анализ диаграммы (рис. 3) показывает, что рост значений радиусов тел качения приводит к снижению величины скоростей скольжения. Различия в видах кривых скоростей скольжения объясняются особенностями состава структуры каждого вида механизма с ЗСТК. Вид кривой 1 соответствует наличию в структуре механизма на горизонтальной оси симметрии максимального и минимального тел качения (рис. 1а). Особенность кривой 2 является следствием расположения на горизонтальной оси симметрии только максимального тела качения (рис. 1б). Кривая скоростей скольжения 3 соответствует наличию на горизонтальной оси симметрии только минимального тела качения (рис. 1в), а для кривой 4 характерно отсутствие на горизонтальной оси симметрии и максимального и минимального тел качения (рис. 1г). Сокращение числа тел качения вызывает рост величин скоростей скольжения двойных точек контакта тел качения с дорожкой качения наружного кольца для любого вида симметричной структурной схемы механизма с ЗСТК с диаметрами разной величины. При принятых условиях расчета минимально возможные значения скоростей скольжения имеют место для кривой 1 (рис. 3), что объясняется наличием больших величин радиусов тел качения при схожем их количестве в структуре механизма с замкнутой системой тел качения. Максимально возможные значения скоростей скольжения соответствуют кривой 3, что является следствием уменьшения величин радиусов тел качения при том же их числе. В то же время при принятых условиях значения скоростей скольжения точек контакта звеньев механизма с ЗСТК лежат в интервале 57,7-84,05 м/c.
Заключение. В результате получена формула для расчета величин скоростей скольжения точек контакта тел качения с дорожкой качения наружного кольца для любого вида симметричной структурной схемы механизма с ЗСТК с диаметрами разной величины при ведущем наружном кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Установлен характер изменения и диапазон возможных значений скоростей скольжения при заданных условиях. Это позволяет обеспечить работоспособность приводов технологического оборудования, разработанных на базе механизма с ЗСТК посредством расчета значения нагружающей внешней силы, а также определить передаточное отношение и коэффициент полезного действия механизма.
Рецензенты:
Меновщиков В.А., д.т.н., профессор, профессор кафедры «Прикладная механика», ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Еркаев Н.В., д.ф-м.н., профессор, профессор кафедры «Прикладная механика», ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.



