При диффузионном режиме протекания реакции восстановления металла из оксида диффузионный поток определяется известным уравнением
![]() , (1)
, (1)
где b – коэффициент массопереноса, м/с; С, С* – концентрация вещества в объеме и на границе раздела фаз, моль/м3.
Коэффициент массопереноса b в соответствии с теорией обновления поверхности [1] определяется из уравнения ![]() , (2)
, (2)
где D – коэффициент диффузии, м2/c; U – скорость конвективного потока, м/с; l – характерный размер конвективного потока, м.
При расчете коэффициента массопереноса сделали два допущения.
1. Отношение скоростей потоков металла и шлака обратно пропорционально динамической вязкости ![]() , (3)
, (3)
где hМе hШл – динамическая вязкость металла и шлака, Па×с.
2. Отношение характерных размеров конвективных потоков металла и шлака прямо пропорционально отношению условных высот металла (hМе) и шлака (hшл)
![]() , (4)
, (4)
где mМе и mшл – масса металла и шлака, кг; ρМе, ρшл – плотность металла и шлака, кг/м3.
Принятые допущения позволяют учитывать существенные условия протекания процесса – вязкость шлака и его количество.
Вязкость шлака (hшл) определяем по уравнениям, связывающим основность и вязкость шлака. Уравнения связи получены в результате обработки данных, приведенных автором [2]. Повышение основности свыше 2,5 – область гетерогенных шлаков, в которых затруднены диффузионные процессы. Получены зависимости для температур 1500 и 1600 °С (рис. 1).
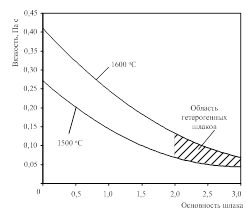
Рисунок 1 – Зависимость вязкости шлака от его основности
hшл = 0,0062B2 – 0,1069B + 0,511, (5)
hшл = 0,00664B2 – 0,0893B + 0,3543, (6)
где В – основность шлака.
Скорость окисления восстановителя при введении на поверхность шлакового расплава для случаев лимитирования процесса диффузией элемента-восстановителя к поверхности раздела фаз металл/расплав и оксидов взаимодействующих элементов в шлаковом расплаве можно рассчитать по уравнениям применительно к марганцу и кремнию:
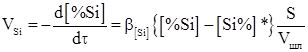 , (7)
, (7)
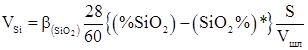 , (8)
, (8)
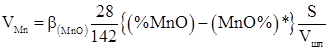 , (9)
, (9)
где![]() – коэффициенты массопереноса, м/с; (% SiO2), (% MnO) – концентрация SiO2 и MnO в шлаке соответственно, масс. %; [% Si] – концентрация кремния в ферросилиции, масс. %; (% SiO2)*, (% MnO)* – равновесные концентрации SiO2 и MnO в шлаке соответственно, масс. %; [Si] – концентрация кремния в ферросилиции, масс. %; [Si]* – равновесная концентрация кремния, масс. %; Ѕ – поверхность раздела фаз, м2; Vшл. – объем шлака, м3.
– коэффициенты массопереноса, м/с; (% SiO2), (% MnO) – концентрация SiO2 и MnO в шлаке соответственно, масс. %; [% Si] – концентрация кремния в ферросилиции, масс. %; (% SiO2)*, (% MnO)* – равновесные концентрации SiO2 и MnO в шлаке соответственно, масс. %; [Si] – концентрация кремния в ферросилиции, масс. %; [Si]* – равновесная концентрация кремния, масс. %; Ѕ – поверхность раздела фаз, м2; Vшл. – объем шлака, м3.
Исходя из предположения о равновесии системы на границе раздела фаз равновесные значения концентраций кремния, марганца, SiO2, MnO определяются по константам равновесия.
Эта система уравнений решается совместно с уравнением константы равновесия методом последовательных приближений.
Время перемещения капель ферросилиция может быть определено из уравнения, с
![]() , (10)
, (10)
где hшл – высота шлакового расплава, м; w – скорость перемещения частиц, м/с.
Для оценки скорости перемещения жидких капель в шлаковом расплаве использовали формулу Рыбчинского-Адамара [3]
![]() , (11)
, (11)
где hм – динамическая вязкость жидкой капли ферросилиция, Па×с; hш – динамическая вязкость оксидного марганецсодержащего расплава, Па×с; r – радиус частиц металла, м; g – ускорение свободного падения, м/с; rм – плотность капли, кг/м3; rш – плотность шлака, кг/м3.
Довосстановление металла из оксидов, находящихся в шлаковом расплаве, идет на границе сталь – оксидный расплав. В этом случае скорость окисления кремния может быть описана уравнением
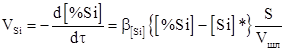 , (12)
, (12)
где b[Si] – коэффициент массопереноса кремния, м/с; [%Si] – концентрация кремния в стали, масс. %; [Si]* – равновесная концентрация кремния, масс. %.
Для связывания образующегося SiO2 вводят свежеобожженную известь.
Скорость растворения дисперсных частиц извести определяется законами конвективной диффузии [4; 5], в частности уравнением
![]() , (13)
, (13)
где (СаО)нас и (СаО) – концентрация оксида кальция в шлаке соответственно у поверхности кусков извести (концентрация насыщения) и в основной массе шлака; S – суммарная поверхность кусков извести, м2; V – объем шлака, м3.
Суммарная поверхность для частиц сферической формы может быть выражена уравнением [5]: ![]() , (14)
, (14)
где М – общая масса частиц, кг; rтв. – плотность частиц, кг/м3; d – диаметр частиц, м.
Для моделирования процесса перемешивания применена модель последовательно расположенных ванн [4]. Изменение во времени концентрации вещества С для последующих ванн выражается уравнением: ![]() , (15)
, (15)
где ri и ri-1 – плотность металла в i-й и i-1 последовательной ванне, кг/м3; Q – поток металла между ваннами, м3/с; Vm – объем одной ванны, м3; ![]() – коэффициент массопереноса вещества через пограничный слой металл-шлак,
– коэффициент массопереноса вещества через пограничный слой металл-шлак, ![]() (где Р – величина, численно характеризующая мощность перемешивания расплава), м/с.
(где Р – величина, численно характеризующая мощность перемешивания расплава), м/с.
Обязательным условием для составления математической модели является выполнение закона сохранения массы, на основе которого составляются мгновенные материальные балансы.
Блок-схему модели условно можно разделить на несколько частей, включающих расчеты следующих показателей – времени взаимодействия раскислителя с оксидами шлака; количества раскислителя, пошедшего на восстановление металла из оксидов шлака; состава металла в объеме и состава оксидного расплава; активности компонентов металлической и шлаковой фаз; скорости реакций взаимодействия раскислителей с оксидами шлака; коэффициентов массопереноса взаимодействующих элементов в металле и шлаке; массы шлаковой и металлической фаз; скорости растворения извести в шлаке; состава металлической и шлаковой фаз; основности шлака.
Структурная схема модели представлена на рисунке 2.
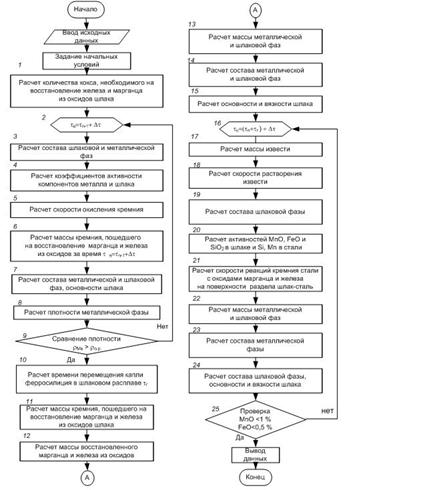
Рисунок 2 – Блок-схема математической модели
Ниже приведены значения заданной погрешности вычисления для различных параметров, принятые при расчетах (табл. 1).
Таблица 1 – Заданная погрешность вычислений опытных параметров
|
Параметр |
Заданная погрешность расчета |
|
Масса металла, кг |
10 |
|
Масса шлака, кг |
10 |
|
Содержание марганца в металле, % |
0,001 |
|
Содержание кремния в металле, % |
0,001 |
|
Содержание марганца в шлаке, % |
1,0 |
|
Содержание кремния в шлаке, % |
1,0 |
|
Содержание железа в шлаке, % |
0,1 |
|
Основность шлака |
0,1 |
|
Масса присадки, кг |
1,0 |
Исходными данными для начала работы системы «Советчик мастера» служат:
- параметры состояния металла: масса на момент времени t1, кг; температура, оС, состав, масс. %;
- параметры состояния шлака: масса окислительного шлака на момент времени t1, кг; основность, единицы; состав, масс. %;
- химический состав кокса;
- параметры ферросилиция: химический состав, масс. %; масса, кг;
- параметры футеровки: масса смываемой за плавку футеровки, кг; состав, масс. %;
- параметры извести: масса извести, кг; время полного растворения извести в шлаке, мин; состав извести, масс. %;
- параметры агрегата, диаметр ванны на уровне шлакового пояса, м, глубина ванны, м;
- дискретность выполнения расчетов, с.
Принцип выполнения расчетов выглядит следующим образом: зная состав металла и шлака, можно рассчитать состав этих фаз после введения кокса. Этот состав является исходным на момент времени t1.
После введения ферросилиция можно рассчитать состав металла и шлака на момент времени t2 = t1 + Dt, где Dt - дискретность выполнения расчетов (блок 1, 2, 3).
В блоке 4 выполняется расчет коэффициентов активности элементов металлической фазы по методике, предложенной авторами [6], и шлаковой фазы [7]. Скорость окисления кремния ферросилиция рассчитывается в блоке 5 по уравнению (12). В блоке 6 производится расчет количества кремния, пошедшего на восстановление оксидов шлака. В блоке 7 производится расчет состава металлической и шлаковой фаз, блок 8 – рассчитывается плотность металлической фазы
Блок 9 – производится сравнение плотности металлической фазы и плотности жидкого шлакового расплава. При выполнении условия rМе > rо.р. переходим к расчету времени перемещения капли металла в оксидном расплаве (блок 10).
В блоке 11 производится расчет массы кремния, которая расходуется на восстановление металлов из оксидов шлака и массы восстановившегося элемента (блок 12). Затем рассчитываются массы металла и шлака путем решения системы трех балансовых уравнений: суммарный материальный баланс, баланс восстановленного элемента, баланс кремния (блок 13), состав металла и шлака (блок 14) и основность и вязкость шлака (блок 15).
Затем производится расчет массы, скорости и времени растворения извести (блоки 17, 18).
Далее выполняется расчет состава шлаковой фазы и коэффициентов активностей компонентов металлической и шлаковой фаз (блоки 19, 20). Активности элементов в металлической фазе рассчитывали с использованием параметров взаимодействия первого порядка, а активности компонентов шлаковой системы оценивали по методике, разработанной авторами [6], и скорости реакции восстановления оксидов, растворенных в стали.
После прохождения блока 20 производится расчет скоростей реакции восстановления металлов из оксидов шлака кремнием, растворенным в стали (блок 21). Далее производится расчет массы и состава металлической и шлаковой фаз (блок 22, 23, 24).
Вычисления производятся до тех пор, пока содержание металла в виде оксида в шлаковой фазе не будет меньше заданной величины точности расчета по данному компоненту.
Для доказательства адекватности модели провели опытные плавки на агрегате «ковш-печь» ОАО «НкМК». Плавление и окислительный период плавки проводили в соответствии с действующей в цехе технологической инструкцией. После выпуска плавки из печи ковш с металлом подавали на агрегат «ковш-печь», где производили замер количества шлака в ковше. После этого на поверхность шлака присаживали коксовую мелочь в количестве 50 – 100 кг и делали выдержку 10–20 мин. Затем присаживали ферросилиций ФС65, ФС75 в количестве, обеспечивающем содержание кремния в стали ближе к верхнему пределу. Одновременно с присадкой кремния вводили известь в количестве, обеспечивающем получение жидкоподвижных шлаков. Присадку материалов производили в условиях перемешивания металла инертным газом. Длительность периода обработки составляла 40–70 мин. В ходе экспериментов контролировали химический состав стали путем отбора проб металла и шлака с хронометрированием всех технологических операций.
Исходные данные каждой плавки были введены для расчета в программу «Советчик мастера». Результаты изменения содержания марганца и кремния по ходу некоторых плавок в отобранных пробах металла и содержание марганца и кремния, полученные расчетным путем для тех же контрольных точек по времени, приведены в таблице 2.
Таблица 2 – Изменение содержания марганца и кремния при выплавке стали марки 25Г2С, %
|
№ плавки |
№ * пробы |
Опытные плавки |
Расчетные данные |
Невязка |
|||
|
Mn |
Si |
Mn |
Si |
Mn |
Si |
||
|
1 |
1 |
0,98 |
0,85 |
1,01 |
0,90 |
0,02 |
0,05 |
|
2 |
1,11 |
0,75 |
1,15 |
0,70 |
0,04 |
0,04 |
|
|
3 |
1,35 |
0,69 |
1,36 |
0,74 |
0,01 |
0,05 |
|
|
4 |
1,45 |
0,66 |
1,46 |
0,70 |
0,01 |
0,04 |
|
|
5 |
1,47 |
0,64 |
1,46 |
0,70 |
0,01 |
0,06 |
|
|
2 |
1 |
0,94 |
0,86 |
0,98 |
0,92 |
0,04 |
0,06 |
|
2 |
1,07 |
0,77 |
1,12 |
0,80 |
0,05 |
0,03 |
|
|
3 |
1,31 |
0,63 |
1,33 |
0,70 |
0,02 |
0,06 |
|
|
4 |
1,39 |
0,61 |
1,41 |
0,68 |
0,02 |
0,07 |
|
|
5 |
1,42 |
0,60 |
1,41 |
0,68 |
0,02 |
0,08 |
|
|
3 |
1 |
1,22 |
1,10 |
1,18 |
0,72 |
0,04 |
0,03 |
|
2 |
1,29 |
0,89 |
1,25 |
0,82 |
0,04 |
0,07 |
|
|
3 |
1,37 |
0,79 |
1,33 |
0,77 |
0,02 |
0,02 |
|
|
4 |
1,47 |
0,70 |
1,48 |
0,75 |
0,01 |
0,05 |
|
|
5 |
1,47 |
0,70 |
1,48 |
0,75 |
0,01 |
0,05 |
|
|
* - пробы 1, 2, 3, 4, 5 – рафинировочные, взятые через 10, 20, 30, 40 и 60 мин после присадки ферросилиция. |
|||||||
Невязка содержания для марганца равна 0,01–0,04%, а для кремния 0,01–0,08%. Относительная ошибка составляет 2–4% для марганца, а для кремния – 6–8%, что находится в допустимых пределах (не более 10%).
Таким образом, можно сказать, что разработанная модель адекватно отражает основные особенности рассматриваемого процесса и позволяет спрогнозировать процесс восстановления металлов из оксидов, а также оценить окисленность шлака.
Рецензенты:
Сапожков С.Б., д.т.н., профессор, заведующий кафедрой естественно-научного образования Юргинского технологического института (филиал) Томского политехнического университета, г. Юрга.
Сенкус В.В., д.т.н., профессор кафедры экологии и техносферной безопасности, Новокузнецкий институт (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Кемеровский государственный университет», г. Новокузнецк.



