Введение
Привод исполнительных органов является важным элементом в структуре дозаторных систем, влияющий на их динамические характеристики.
В таких системах широко применяются электромеханические приводы на основе кривошипно-ползунных, шнековых, кулачковых и других механизмов [3].
В частности, применение кулачкового механизма позволяет сформировать закон движения исполнительного органа, обеспечив плавность работы, фиксированное время холостого и рабочего ходов, что существенно влияет на качество и технологичность процесса дозирования.
При этом синтез конструкторско-технологических параметров дозаторной системы, удовлетворяющих заданным требованиям, является важной и актуальной задачей.
Целью данной работы является исследование динамики и оценка ее влияния на характеристики дозаторной системы с кулачковым приводом.
Материалы и методы исследования
Нагнетание дозируемой жидкости на рабочем ходу и ее всасывание из бака на холостом ходу происходит с помощью плунжера (толкателя), контактирующего с кулачком (рис. 1), профиль которого обеспечивает заданный закон возвратно-поступательного движения исполнительного органа. Кулачок приводится во вращение электродвигателем.
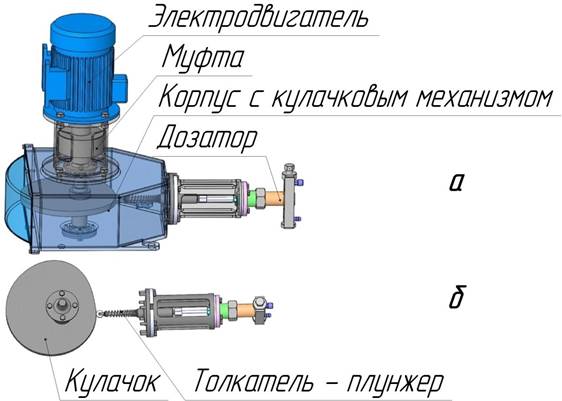
Рис. 1. Дозаторная система с кулачковым приводом
а – общий вид; б – кулачковый механизм
Моделирование динамики системы дозирования (рис. 1) осуществляется на основе структурно-функциональной схемы [6], фрагмент которой представлен на рис. 2.
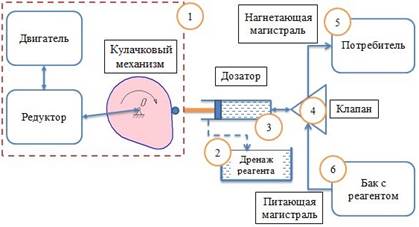
Рис. 2. Структурно-функциональная схема дозаторной системы с кулачковым механизмом
Соответствующая расчетная схема с основными параметрами изображена на рис. 3.
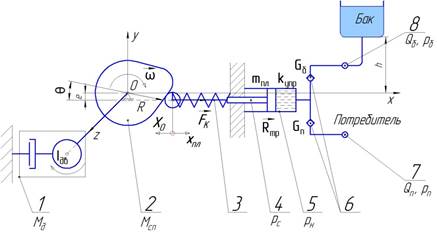
Рис. 3. Расчетная схема дозаторной системы с кулачковым приводом
Здесь и далее приняты следующие обозначения: QП, QБ – соответственно расход жидкости поступающей на потребитель и из бака, м3/с; pН, pП, pБ – соответствующие давления в напорной камере, на потребителе и в баке, МПа; xПЛ – перемещение плунжера, м; 
– скорость плунжера, м/с; 
– угол поворота кулачка, рад; 
– угловая скорость кулачка, рад/с; MД, MСП – соответственно движущий момент электродвигателя и момент сопротивления на кулачке, Н·м; FК – осевое усилие со стороны кулачка на толкатель (плунжер), Н; h – высота столба жидкости в баке с реагентом, м.
Математическая модель динамики дозатора формируется при следующих допущениях: жидкость мало сжимаема; материал стенок цилиндра дозатора податлив; потери в камере дозатора равны нулю; давления на потребителе и в баке, постоянны.
Уравнения, описывающие работу дозаторной системы в соответствии с расчетной схемой рис. 3 при учете динамической взаимосвязи всех её элементов [1], представлены соотношениями 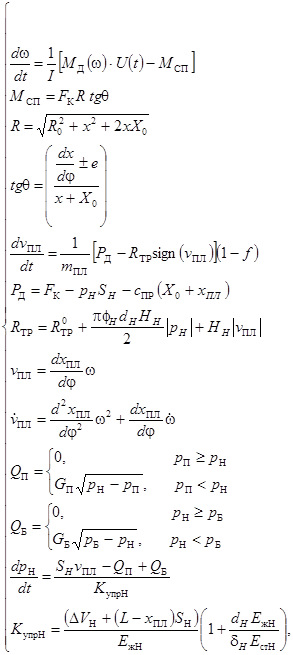(1):
(1)
где 
– приведенный к кулачковому валу момент инерции двигателя, редуктора (при его наличии) и кулачка, кг·м2; i – передаточное число редуктора; U(t) – функция управления (1 – включено, 0 - выключено); R, R0 - текущий и начальный радиус кулачка, м; X0 – положение толкателя наиболее близкое к центру вращения, м; e - эксцентриситет кулачка, м; q – угол давления [4, 5], рад; SН - площадь сечения цилиндра, м2; dН, d¢Н, dН – диаметры цилиндра, плунжера и толщина стенки цилиндра, м; 
– мертвый объем полости дозатора, м3; L – ход плунжера, м; EжН, EстН – модули упругости жидкости и материала стенки цилиндра, МПа; KупрН – коэффициент упругости жидкости и материала стенки цилиндра дозатора, м3/МПа; mПЛ – масса плунжера, кг; PД – движущая сила на плунжере, Н; 
– сила трения в манжетных уплотнениях при отсутствии давления, Н; RТР - суммарная сила трения, Н; fН – коэффициент трения в манжетах; сПР – жесткость пружины, Н/м; HН – высота манжетного уплотнения в цилиндре, м; GП, GБ – проводимость клапанов [2], м4·с-1·Н-0,5.
Соотношения (1) характеризуют дозаторную систему как единую взаимосвязанную электрогидромеханическую структуру.
Выразив из (1) значение осевой силы FК и введя обозначения 
, 
, 
, уравнения динамики при заданном законе движения исполнительного органа 
принимают вид:
(2)
где: 
; 
;
.
По заданным начальным условиям y1,0, y2,0, y3,0 определяются S(y1,0) и характеристики алгебраических соотношений системы (2). Затем интегрируются остальные дифференциальные уравнения, формируя последующие приближение и т.д.
Математическое моделирование динамики дозатора осуществляется в системе Matlab с помощью разработанного программного комплекса на основе метода Рунге – Кутта 4 и 5 порядков по схеме Dormand and Prince (автоматический выбор шага) [7].
В процессе моделирования при заданном законе движения плунжера с учетом динамической характеристики двигателя определяются усилия и момент сопротивления в кулачковом механизме, давление жидкости в камере дозатора и соответственно расходы жидкости в соответствии с условиями функционирования клапанов.
Результаты исследования и их обсуждение
Результаты моделирования представляются в виде таблиц значений и графических диаграмм параметров и характеристик дозаторной системы.
Рис. 4, 5 иллюстрируют результаты одного из расчетов при следующих основных исходных данных: давление в магистрали потребителя 40 МПа (400 атм.), ход поршня 60 мм, кулачок центральный с начальным радиусом 0,12 м, закон движения толкателя – полиномиальный девятой степени [5].
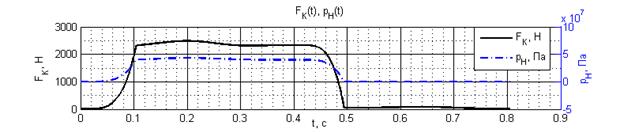
Рис. 4. Графики осевого усилия со стороны кулачка на толкатель и давления дозируемой жидкости в камере дозатора
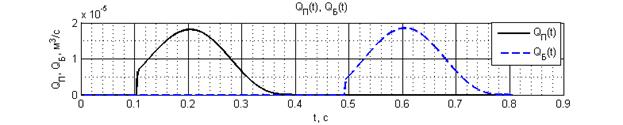
Рис. 5. График расходов клапанов дозатора
Анализируя полученные данные рис. 4, 5 видно, что принятый закон движения исполнительного органа, реализуемый формой профиля кулачка, обеспечивает плавный рост усилия на плунжере и давления в камере дозатора. Вследствие этого осуществляется безударное открытие клапана при дозировании на рабочем ходу и соответствующее открытие клапана на холостом ходу при всасывании дозируемой жидкости.
Заключение
Предложенная математическая модель и программный комплекс позволяют осуществить направленное исследование динамики дозаторных систем с кулачковым приводом. Тем самым появляется возможность выбора оптимальных конструктивно-технологических параметров, удовлетворяющих требуемым критериям качества функционирования дозаторных систем.
Рецензенты:
Иванов В.А., д.т.н., профессор, зав. кафедрой МСИ Пермский национальный исследовательский политехнический университет, г.Пермь.
Матыгуллина Е.В., д.т.н., профессор кафедры МТиКМ Пермский национальный исследовательский политехнический университет, г.Пермь.