Введение
Многолетний опыт эксплуатации пароперегревателей паровых котлов показал, что эти поверхности нагрева являются одним из самых ненадежных элементов котельных агрегатов. 80 – 85 % аварийных остановов парогенераторов происходит в результате выхода из строя данных поверхностей нагрева [1]. В связи с этим исследования нестационарных температурных режимов пароперегревателей в целях повышения их долговечности является одной из актуальных задач теплоэнергетической отрасли.
Также следует отметить, что основными методами изучения температурных режимов являются экспериментальный метод и метод теплофизического и гидравлического расчетов [2-5]. Использование экспериментального метода требует больших финансовых затрат и соответствующего оборудования, а результаты теплофизического и гидравлического расчетов являются неточными. В связи с этим использование методов численного моделирования для этих целей является наиболее рациональным способом, так как результаты, полученные при правильной физико-математической постановке, являются наиболее достоверными.
Целью настоящей работы является численное моделирование нестационарного температурного режима пароперегревателя парогенератора БКЗ-75-39.
Метод исследования
В качестве метода исследования нестационарного температурного режима пароперегревателя использован способ численного моделирования. Для этого сформулирована физико-математическая постановка задачи, описанная ниже.
Физическая постановка задачи
Объектом исследования в данной работе является участок трубы пароперегревателя парогенератора БКЗ-75-39 (рис. 1). Для анализа температурного режима пароперегревателя используется двумерное нестационарное уравнение теплопроводности цилиндрической стенки с соответствующими начальным и граничными условиями. Для расчета температур на внешних границах цилиндра конечных размеров используются граничные условия первого и третьего рода. В частности, на левой и правой границах принимаются граничные условия третьего рода, а на верхней и нижней границах – граничные условия первого рода. Исходные данные пароперегревателя взяты из паспорта котла. При постановке задачи приняты следующие основные допущения:
1. Теплофизические параметры дымовых газов, материала стенки труб и пара считаются постоянными и известными величинами.
2. Среды, омывающие цилиндрическую поверхность снаружи и протекающие внутри нее, несжимаемы с гидродинамическим и термически стабилизированным течением. Теплота трения не учитывается.
3. Рассматривается прямой круглый вертикальный участок трубы змеевика пароперегревателя с определенными геометрическими характеристиками без внутренних дефектов во внутрикристаллической структуре (наличие трещин и т.п.).
4. В математической постановке задачи, вследствие относительной малости градиентов температур по координате φ, частные производные температуры от этой величины не учитываются.
Математическая постановка задачи
Распределение температуры в цилиндрической стенке трубы описывается ниже:
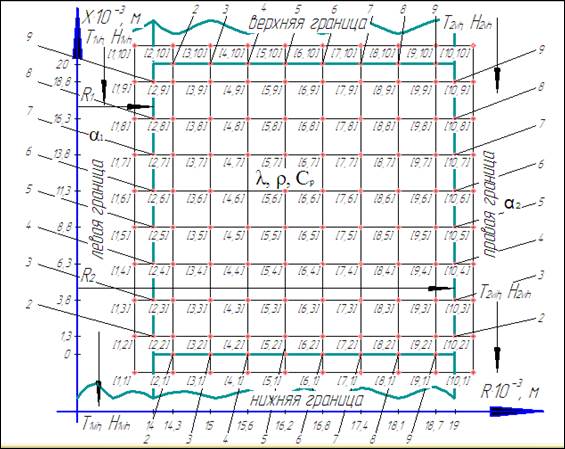
Рис. 1. Схематичное изображение исследуемого объекта с температурной сеткой
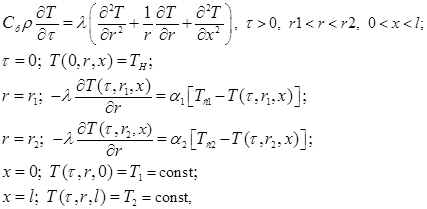 (1)
(1)
где Cp – теплоемкость стали, Дж/(кг·°С); ρ – плотность стали, кг/м3; λ – коэффициент теплопроводности стали, Вт/(м·°С); α1,α2 – соответственно коэффициенты теплоотдачи от дымовых газов к внешней поверхности и от внутренней поверхности к пару, Вт/(м2·K); Tс1,Tс2 – соответственно температура дымовых газов и пара, °С; T1,T2 – температура стенки на верхней и нижней границе °С.
Температуры на верхней и нижней границе цилиндрической стенки определяются на основе уравнения теплового баланса с помощью следующих выражений [6]:
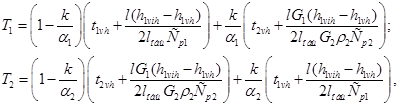 (2)
(2)
где k – коэффициент теплопередачи цилиндрической стенки, Вт/(м·°С); lобщ – общая длина трубы, м.
Для решения приведенной математической модели используется метод конечных разностей, а именно схема расщепления [7, 8] с применением разностной аппроксимации дифференциальных операторов. С целью проверки достоверности полученные результаты подставляются в уравнение теплопроводности и краевые условия однозначности.
Результаты
В ходе решения поставленной задачи были получены следующие результаты:
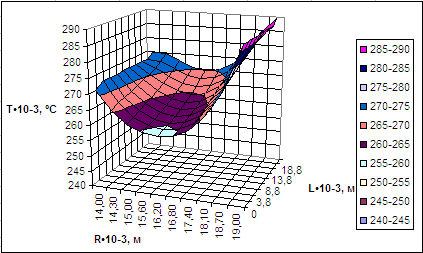
Рис. 2. Распределение температур в цилиндрической стенке при τ = 5 с
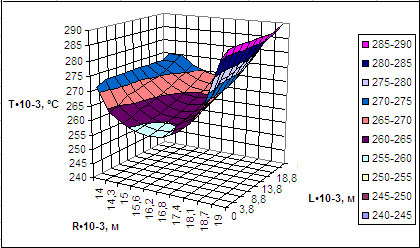
Рис. 3. Распределение температур в цилиндрической стенке при τ = 5 с, полученное в ходе проверки
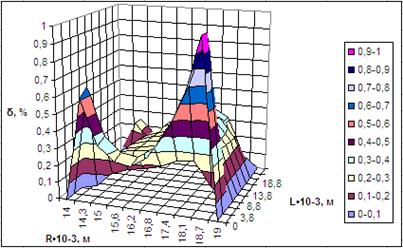
Рис. 4. Поле погрешностей расчета
Обсуждение результатов
Как видно из полученных результатов, представленных на рис. 2 и 3, распределения температур в цилиндрической стенке имеют максимальные значения температур на правой и левой границе. При этом минимальные значения температур находятся в середине стенки. Данное распределение температур обусловлено прогревом поверхности нагрева в начальный момент времени дымовыми газами (970 ºС) на правой границе и паром (256 ºС) на левой. Так как в нашем случае меньшие градиенты температур находятся в центральной части стенки, то соответственно тепло будет распространяться от левой и правой границы к середине поверхности нагрева. Что же касается граничных температур, то здесь выполняется условие сохранение энергии (закон Ньютона-Рихмана). Отсюда следует, что повышенные температуры на правой границе по сравнению с левой границей обусловлены большим количеством теплоты переданной от дымовых газов к этой поверхности.
При сравнении температурных полей на рис. 2 и 3, полученных в результате реализации физико-математической модели и при выполнении проверки, нетрудно заметить, что качественно они не отличаются, а количественное их отличие не превышает 1 %. Данная погрешность вызвана неточностью значений физических свойств металла, используемых при расчете, а также погрешностью аппроксимации.
Вывод
Как видно из полученных результатов, погрешность расчетов не превышает 2 %. Отсюда следует, что данная физико-математическая модель применима для вычисления температурного режима пароперегревателя и в дальнейшем будет использоваться в целях исследования нестационарных режимов этих поверхностей нагрева.
Рецензенты:
Борисов Б.В., д.ф-м.н., профессор кафедры ТПТ, ЭНИН, Национальный исследовательский Томский политехнический университет, г. Томск.
Голдаев С.В., д.ф-м.н., профессор кафедры ТПТ, ЭНИН, Национальный исследовательский Томский политехнический университет, г. Томск.



