Введение
В настоящее время многие электрофизические устройства, работающие при импульсных электромагнитных полях, имеют такие массивные проводники, как токоподводящие шины, электромагнитные экраны, обрабатываемые электромагнитным давлением металлические детали, роторы и обмотки импульсных электромашинных генераторов. При экспериментальном и теоретическом исследовании таких устройств возникает необходимость учета поверхностного эффекта в массивных проводниках. Для упрощения анализа, особенно при оптимизации, могут быть использованы формулы для расчета эквивалентных параметров поверхностного слоя (скин-слоя) массивных проводников, которыми являются толщина скин-слоя и его усредненная температура, активное сопротивление и внутренняя индуктивность проводника, максимальное давление электромагнитного поля на проводник [2–4]. Поэтому расчет эквивалентных параметров скин-слоя массивных проводников при импульсном электромагнитном поле представляется актуальной задачей.
Цель данной работы заключается в получении формул для инженерного расчета эквивалентных параметров скин-слоя массивных проводников в переходном режиме при заданном импульсном электромагнитном поле.
Допущения
Для получения расчетных формул сделаем следующие допущения.
1. Скин-слой проводника характеризуется постоянными величинами магнитной проницаемости 
(Гн/м), удельной проводимости 
(1/Ом·м) и усредненной температуры 
(°С), причем [7]:
, (1)
где 
– удельная проводимость при температуре 
, которая была у проводника до воздействия импульсного электромагнитного поля;
– постоянный температурный коэффициент (1/°С).
2. Нагрев скин-слоя происходит адиабатно без учета теплообмена с окружающей средой при постоянных значениях удельной теплоемкости С (Дж/кг·°С) и объемной плотности 
(кг/м3) проводника [7].
3. Размеры массивных проводников и радиусы кривизны их поверхности существенно превосходят глубину проникновения в них импульсного электромагнитного поля, поэтому будем исходить из представления о плоской одномерной электромагнитной волне, проникающей в проводящее полупространство перпендикулярно его поверхности и полностью затухающей в его теле [2; 6].
4. Импульсное электромагнитное поле задается магнитной напряженностью на поверхности проводника 
– это импульсная функция времени t длительностью 
.
5. Импульсное электромагнитное поле в проводнике имеет нулевые начальные условия, т.е. при t=0 поле в проводнике полностью отсутствует, даже если 
.
Методика расчета
Совместим границу проводящего полупространства с плоскостью x0y в декартовой системе координат (рис. 1), так что для плоской одномерной электромагнитной волны векторы напряженностей электрического 
и магнитного 
полей имеют по одной составляющей, зависящих от координаты z и времени t [2; 6]:
; 
,
где 
– единичные векторы, направленные по осям x и y соответственно.
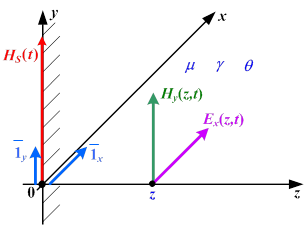
Рис. 1. Проводящее полупространство: 
– магнитная напряженность на поверхности проводника
В этом случае процесс проникновения электромагнитного поля в проводник описывается следующим уравнением [2; 6]
(2)
при плотности тока
. (3)
Примем, что при 
электромагнитная волна полностью затухает, тогда граничные условия имеют вид:
. (4)
При нулевых начальных условиях воспользуемся спектральным (частотным) методом и по одностороннему прямому преобразованию Фурье найдем спектральную функцию магнитной напряженности на поверхности проводника [5]:
, (5)
где 
и 
– амплитудная и фазовая спектральные характеристики импульса магнитной напряженности на поверхности проводника;
– мнимая единица.
При этом уравнения (2, 3) в комплексной форме примут вид [2; 6]:
; 
, (6)
где 
и 
– комплексные амплитуды магнитной напряженности и плотности тока в функции координаты z и угловой частоты 
.
Решение уравнений (6) с учетом (4, 5) будет следующим [2; 6]:
; (7)
, (8)
где постоянная распространения электромагнитной волны равна
(9)
при эквивалентной глубине проникновения синусоидальной электромагнитной волны с угловой частотой в проводящее полупространство
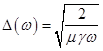. (10)
Далее на основании обратного преобразования Фурье [5] с использованием формул (7–10) можно определить магнитную напряженность и плотность тока в проводящем полупространстве:
; (11)
. (12)
Затем находим усредненные во времени значения мощности тепловых потерь [2; 3; 6]
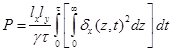(13)
и энергии магнитного поля
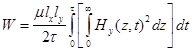, (14)
lx и ly – размеры проводника по осям x и y соответственно (рис. 1).
При среднеквадратичном значении напряженности на поверхности проводника
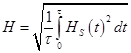(15)
согласно закону полного тока [6] имеем для тока i(t) среднеквадратичное значение
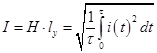. (16)
При активном сопротивлении
(17)
и внутренней индуктивности
(18)
запишем усредненные значения мощности тепловых потерь
, (19)
и энергии магнитного поля
, (20)
где 
– эквивалентные толщины скин-слоя для расчета сопротивления и внутренней индуктивности соответственно.
Из равенства (13, 19) и (14, 20), с учетом (15–18), определяем эквивалентные толщины скин-слоя для расчета сопротивления
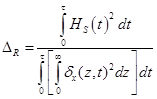(21)
и внутренней индуктивности
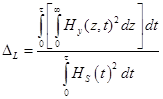. (22)
При адиабатном нагреве скин-слоя толщиной 
можно записать уравнение [7]:
, (23)
тогда с учетом (1, 13, 21) получаем уравнение для усредненной температуры этого слоя
(24)
при расчетном параметре (1/°С):
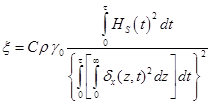. (25)
Уравнение (24) решается методом итераций: задаемся температурой ; по (1) находим ; по (12) определяем 
; по (25) рассчитываем 
; по (24) получаем ; по (1) находим и т.д. Расчеты ведем до повторения значений температуры .
Давление электромагнитного поля на проводник, которое направлено вдоль оси z (рис. 1), найдем следующим образом [2]:
, (26)
причем это давление имеет некоторое максимальное значение 
, которое должно быть меньше допустимого значения 
, исходя из механической прочности проводника.
Результаты расчета
При угловой частоте 
радиоимпульса напряженности с синусным заполнением
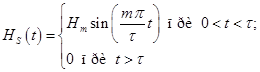(27)
при 
(А/м); 
(с) по запрограммированным в среде Mathcad [1] формулам (1–27) проведены расчеты эквивалентных параметров массивного проводника из отожженной меди [3; 7]: 
(Гн/м); 
(°С); 
(См/м); 
(1/°С); 
(кг/м3); 
(Дж/кг·°С); 
(МПа) при 
(°С).
Рассчитанные эквивалентные параметры массивного проводника из отожженной меди приведены в таблице 1, где также указаны относительные эквивалентные толщины скин-слоя, найденные в [3] операторным методом и в [4] численным методом, причем в таблице обозначены для синусоидального электромагнитного поля с угловой частотой 
в установившемся режиме: глубина проникновения 
; максимум давления 
(МПа).
Таблица 1
Эквивалентные параметры массивного медного проводника
|
Расчет |
Из [3] |
Из [4] |
|||||||||
|
m |
|
|
|
|
|
|
|
|
|
||
|
– |
°С |
– |
мм |
– |
– |
– |
– |
– |
– |
||
|
0,5 |
40 |
1,19 |
14 |
0,84 |
0,49 |
– |
– |
1,35 |
0,25 |
||
|
1 |
40 |
1,04 |
9,74 |
1,20 |
0,71 |
1,43 |
0,56 |
1,55 |
0,50 |
||
|
1,5 |
70 |
1,18 |
8,42 |
0,92 |
0,56 |
– |
– |
1,15 |
0,45 |
||
|
2 |
75 |
1,06 |
7,35 |
1,02 |
0,60 |
1,12 |
0,54 |
1,20 |
0,50 |
||
|
2,5 |
103 |
1,15 |
6,89 |
0,93 |
0,54 |
– |
– |
1,07 |
0,50 |
||
|
3 |
106 |
1,08 |
6,32 |
1,00 |
0,59 |
1,09 |
0,52 |
1,05 |
0,50 |
||
|
3,5 |
135 |
1,14 |
6.11 |
0,93 |
0,54 |
– |
– |
1,04 |
0,50 |
||
|
4 |
139 |
1,06 |
5,74 |
0,98 |
0,57 |
1,06 |
0,52 |
1,03 |
0,50 |
||
|
4,5 |
167 |
1,13 |
5,63 |
0,94 |
0,54 |
– |
– |
1 |
0,50 |
||
|
5 |
171 |
1,07 |
5,37 |
0,98 |
0,56 |
1,04 |
0,53 |
1 |
0,50 |
||
На рис. 2 для напряженности (27) при m=5 приведены расчетные графики относительных временных зависимостей магнитной напряженности и плотности тока на поверхности проводника, где также указан график давления электромагнитного поля на проводник.
Заключение
1. Предложена методика определения эквивалентных параметров скин-слоя массивных проводников с учетом их адиабатного нагрева при импульсном электромагнитном поле, которая основывается на частотном методе и может использоваться для расчета токоподводящих шин, электромагнитных экранов, обрабатываемых электромагнитным
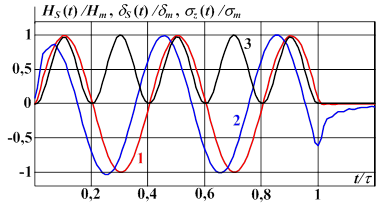
Рис. 2. Относительные временные зависимости: 1 – магнитная напряженность 
;
2 – плотность тока на поверхности проводника 
; 3 – давление электромагнитного поля на проводник 
; 
– максимальная плотность тока
давлением металлических деталей, роторов и обмоток импульсных электромашинных генераторов.
2. Разработанная методика получена на основе уравнений электромагнитного поля, которые могут быть запрограммированы, например, в среде Mathcad для инженерного расчета эквивалентных параметров массивных проводников импульсных электрофизических устройств при их автоматизированном проектировании.
3. Определяемые толщина скин-слоя и его усредненная температура, активное сопротивление и внутренняя индуктивность проводника, максимальное давление электромагнитного поля на проводник зависят от амплитуды, длительности и формы импульса магнитной напряженности на поверхности проводника.
4. Достоверность предлагаемой методики, основывающейся на частотном методе, подтверждается приемлемым совпадением результатов расчета эквивалентных толщин скин-слоя с результатами, полученными операторным и численным методами.
Работа выполнена в рамках государственного задания «Наука» 7.2826.2011 «Разработка и создание гибридной модели энергоблоков электростанций».
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Канев Ф.Ю., д.ф.-м.н., ведущий научный сотрудник Института оптики атмосферы им. В.Е. Зуева СО РАН, г. Томск.