Введение
Эффективность операций, реализуемых при помощи технологического оборудования, напрямую связана с формой рабочей поверхности исполнительного органа и видом движения, им совершаемого, а также рационально подобранными геометрическими параметрами механизма привода. Повышение эффективности этих операций является актуальной задачей, решение которой возможно обеспечить посредством использования механизмов с замкнутой системой тел качения (ЗСТК), позволяющих реализовать сложное движение выходного звена при минимально возможном числе подвижных звеньев. Механизмы с ЗСТК обладают структурой, которая образована совокупностью двух колец с дорожками качения, сепаратора (водило) и тел качения с диаметрами равной или разной величины, которые могут обладать рабочими поверхностями с выступами (зубчатые) [1; 2] или гладкими поверхностями (фрикционные) [3-10].
Коллектив авторов проводит теоретические и экспериментальные исследования геометрических и кинематических параметров исполнительных механизмов технологического оборудования, разработанного на базе механизмов с ЗСТК с диаметрами разной (эксцентриковые) [1-3; 6; 7; 9; 10] или равной (соосные) [4-6; 8; 10] величины. В ходе исследований установлено: если замкнутая система тел качения обладает диаметрами равной величины, то задача определения номинальных значений геометрических параметров механизмов с ЗСТК должна решаться при начальных условиях, что исходные параметры являются постоянными и принимают значения больше нуля
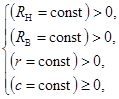(1)
где RВ и RН – радиусы концентрически расположенных дорожек качения внутреннего и наружного колец; r и c – радиус тел качения и зазор между ними.
Авторами установлено, что рассматриваемая задача является не линейной и при начальных условиях (1) может не иметь решения. Для исключения подобных случаев необходима корректировка системы (1) посредством ввода поправки в расчет номинальных значений геометрических параметров, считая, что один из исходных параметров является величиной переменной [3]. Вариация значениями радиуса тел качения и зазора не позволяет достичь требуемого результата. В этом случае получаем, что решение поставленной задачи имеет два возможных направления ввода поправки, т.е. либо 
, либо 
.
Настоящее исследование проводится с целью разработки алгоритма корректировки расчета номинальных значений геометрических параметров механизмов с замкнутой системой тел качения с диаметрами равной величины для любого вида симметричной структурной схемы посредством ввода поправки в расчет по радиусу дорожки качения внутреннего кольца. Полученные результаты позволят повысить эффективность расчета номинальных величин геометрических параметров механизмов с ЗСТК и точность получаемых результатов.
Методы исследования, применяемые в настоящей работе, основаны на принципах геометрического анализа механизмов при использовании положений геометрии, свойств тригонометрических функций и остроугольных разносторонних треугольников.
В соответствии с вышеуказанной целью начальные условия системы (1) примут следующий вид
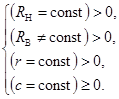(2)
Система (2) позволяет получить два возможных варианта структуры механизма с ЗСТК с диаметрами равной величины, как при наличии, так и при отсутствии зазора между телами качения (рис. 1).
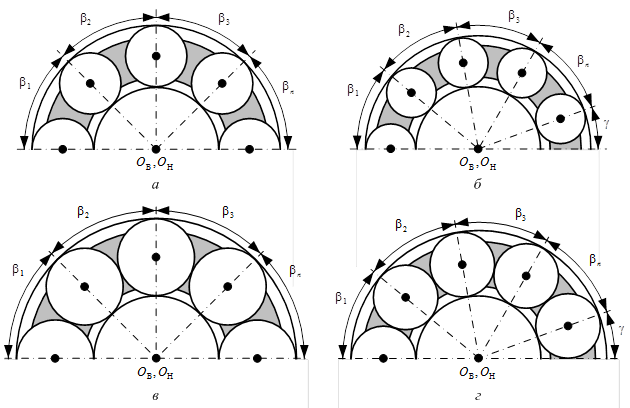
Рис. 1. Виды симметричных структурных схем механизмов с ЗСТК с диаметрами равной величины. Тела качения расположены: а, б - с зазором; в, г - без зазора;
ОВ, ОН – центры дорожек качения колец; b1, b2, b3, bn , g – углы положения тел качения
При исходных условиях (2) радиус дорожки качения внутреннего кольца определим в соответствии с работами [4; 8], по формуле
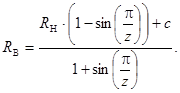(3)
Радиусы дорожек качения наружного и внутреннего колец механизма с ЗСТК рассматриваемого вида (рис. 1) находятся в следующей зависимости
(4)
здесь 
– радиус тел качения.
Подставив (4) в (3) и преобразовав, получим выражение для определения радиуса тел качения при условиях системы (2)
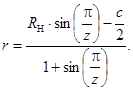(5)
Углы положения тел качения и их число вычислим в соответствии с работами [4; 8]
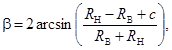(6)
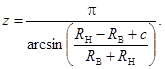(7)
Геометрические параметры, полученные по формулам (3), (5) — (7), должны удовлетворять одному из вариантов условия симметрии механизмов с ЗСТК с диаметрами равной величины в зависимости от числа тел качения на горизонтальной оси симметрии [6]:
два тела качения (рис. 1 а, в) 
(8)
одно тело качения (рис. 1 б, г) 
(9)
где n – число тел качения на угле от 0 до p, bi – угол положения i-го тела качения, g – угол, определяемый согласно рис. 1 б, г.
При не выполнении условий симметрии (8) и (9) необходим ввод поправки в расчет, значение которой определим по выражению
(10)
здесь 
– отрезок, обладающий меньшей длиной из 
или 
.
С целью определения длин отрезков и составим расчетную модель (рис. 2а) механизмов с ЗСТК с диаметрами равной величины при наличии на горизонтальной оси симметрии двух тел качения (рис. 1 а, в).
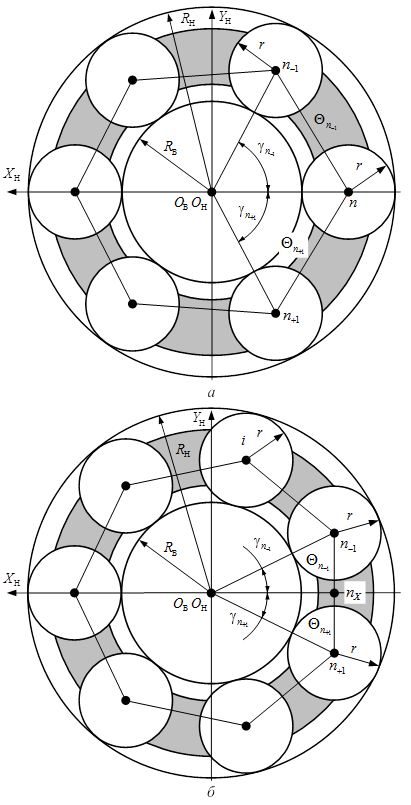
Рис. 2. Расчетная модель для определения длин отрезков 
и 
при наличии на горизонтальной оси симметрии: а – двух тел качения; б – одного тела качения
Из анализа треугольников 
и 
(рис. 2) при 
получим следующие равенства:
(11)
(12)
где 
и 
– углы положения тел качения (рис. 2а).
Углы и в (11) и (12) определим по формуле
(13)
здесь 
определяется по формуле (6).
При наличии на горизонтальной оси симметрии одного тела качения расчетная модель механизмов данного вида будет выглядеть, как представлено на рис. 2б, а длины отрезков и определим по формулам:
(14)
(15)
где и – углы положения тел качения (рис. 2б), определяются по (13).
Корректировка расчета номинальных значений геометрических параметров механизмов с ЗСТК с диаметрами равной величины осуществляется посредством ввода поправки в расчет по радиусу дорожки качения внутреннего кольца. Алгоритм корректировки предполагает следующий порядок действий: согласно начальным условиям (2) радиус дорожки качения наружного кольца оставляем без изменений, а радиус дорожки качения внутреннего кольца изменяем по формуле
(16)
Далее проводим новую итерацию расчета геометрических параметров по формулам (3), (5) — (7). По полученным значениям проверяем условия симметрии (8) или (9). При положительном результате прекращаем вычисления. При отрицательном результате, используя (10) — (15), определяем новое значение поправки, а по (16) проводим корректировку радиуса дорожки качения наружного кольца. Затем повторяем описанные выше действия. Расчет продолжаем до выполнения условия симметрии (8) или (9).
Разработанный алгоритм корректировки расчета номинальных величин геометрических параметров механизмов с ЗСТК прошел апробацию на международной научно-практической конференции (проект Sworld). Используя результаты исследования, авторы разработали программное обеспечение, которое представляет собой программный комплекс «Эксцентрик», зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ) [10].
Заключение. В результате проведенных действий сформированы системы начальных условий. Получены формулы для расчета величины поправки. Разработан алгоритм корректировки расчета номинальных величин геометрических параметров для любого вида симметричной структурной схемы (рис. 1) механизмов с замкнутой системой тел качения с диаметрами равной величины посредством ввода поправки в расчет по дорожке качения внутреннего кольца.
Рецензенты:
Петровский Э.А., д.т.н., профессор, заведующий кафедрой технологических машин и оборудования нефтегазового комплекса, ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Желукевич Р.Б., д.т.н., доцент, профессор кафедры авиационных горюче-смазочных материалов, ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.