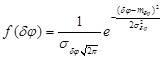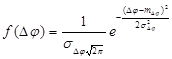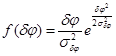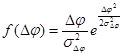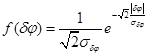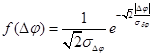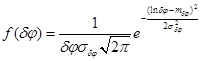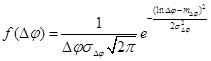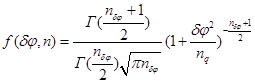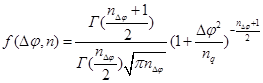Сегодня все более широкое применение находит математическое моделирование различных процессов. Построение модели и получение по ней достоверных результатов становится одной из самых актуальных задач. В связи с этим важной является проблема обеспечения высокого качества результатов экономического исследования, одной из сторон которой является точность используемых в моделировании данных по отношению к фактическим величинам. Случайные ошибки в их измерении, не принимаемые во внимание традиционными методами, в сочетании с естественной случайной ошибкой модели, могут оказывать существенное влияние на результат моделирования. В связи с необходимостью ограничивать множество значений участвующих в анализе или исследуемых переменных появляется риск выйти за допустимые значения переменных в результате накопления таких ошибок. Значит, при моделировании необходимо учитывать такой риск.
Ранее, в работах [3-5], описанная проблема рассматривалась в условиях использования в качестве рассматриваемой модели сначала однофакторной, затем многофакторной линейной регрессионной зависимости, а также в предположении, что случайные ошибки имеют нормальное распределение. Однако в общем случае эти предположения не обязательны.
В данной работе расширен предложенный в [3-5] метод количественного описания риска, возникающего при моделировании с переменными, имеющими критические значения, на случай модели произвольного вида, а также на случай распределенных по различным законам распределения случайных ошибок.
Пусть имеет место некоторый смоделированный процесс 
, зависящий от 
: 
. При описании эконометрической зависимости между указанными переменными будем считать, что существует случайная ошибка модели. Тогда модель процесса примет вид: 
. Кроме того, с учетом некоторых внутренних и внешних факторов, выделим фактическое значение 
, отличающееся от измеренного значения 
на некоторую величину 
: 
. Тогда с использованием модели процесса будет иметь вид:
(1)
Оценочная величина определится следующим образом:
(2)
Предположим, что имеется некоторая допустимая область, внутри которой должны находиться фактические значения . Примерами ситуаций, в которых появляется такая область, являются, например, следующие: 1) множество, на котором возможно использование построенной модели, ограниченно; 2) имеются некоторые критические значения моделируемой величины, возникающие в силу сущности изучаемых явлений; 3) фиксация момента выхода за границы некоторого рубежного множества. Обозначим такую область через 
. Из-за возникновения в процессе использования модели описанной ранее величины выделяется множество 
, отличное от 
.
В зависимости от взаимного расположения ,
и 
относительно допустимых множеств можно выделить несколько ситуаций. Случай 
определим как событие 
. Если выполняется включение 
, то имеет место событие 
. Если эти включения не выполняются, то будем считать, что происходят события 
соответственно.
Так как при использовании модели следует рассматривать все допустимые области, всегда будет иметь место какое-нибудь сочетание событий указанных двух групп.
Полученные комбинации ситуаций можно условно разделить на две группы: безопасные, то есть дающие однозначную, верную информацию, и опасные, подразумевающие ошибочные выводы. К первой группе относятся события 
и 
. Ко второй группе, в силу двойственности информации, следует отнести 
и 
.
Безопасные ситуации не влекут за собой получение недостоверных результатов, так как в этом случае всегда можно проверить работу модели. Таким образом, риск, возникающий при применении зависимости 
, будем понимать как вероятность наступления событий и .
Вероятность наступления одного из них можно вычислить, используя подход, описанный в [2].
Приведем вывод выражения для вычисления вероятности наступления события.
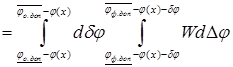, (3)
где 
- совместная плотность распределения отклонений 
.
Аналогично находятся вероятности остальных событий. Ввиду того что вероятность , как правило, оказывается очень малой, вероятность ошибочного решения можно найти как 
.
В работе [3-5] рассматривался случай, при котором все учитываемые при вычислении риска отклонения имели нормальное распределение. Однако в общем случае это предположение может не выполняться. Проанализируем, какой вид примет формула (3) в результате работы с различными распределениями ошибок.
В работе [6] рассматриваются различные законы распределения, которым могут подчиняться случайные ошибки. Адаптируем некоторые выкладки из нее для нашего случая. Результаты представлены в таблице 1.
Таблица 1
|
Распределение |
Распределение |
|
Гаусса
|
Гаусса
|
|
Рэлея
|
Рэлея
|
|
Лапласа
|
Лапласа
|
|
Вейбулла
|
Вейбулла
|
|
Логнормальный
|
Логнормальный
|
|
Стьюдента
|
Стьюдента
|
Таким образом, в каждом из представленных случаев, в виде подынтегральной функции будет выступать совместная функция плотности распределений, совпадающая с одной из представленных в таблице 1.
Рассмотрим теперь подсчет вероятности ошибочных выводов при сочетании ошибок, имеющих разные законы распределения.
Пусть 
и 
имеют лапласовское распределение на бесконечных интервалах. Тогда формула 3 примет вид:
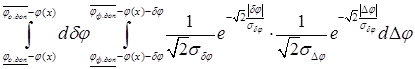
В отличие от рассмотренного ранее в работах [3-5] случая, когда все учитываемые в модели ошибки распределены по нормальному закону и интеграл приходится вычислять приблизительно с помощью численных методов, в этом случае можно получить точное значение интеграла:
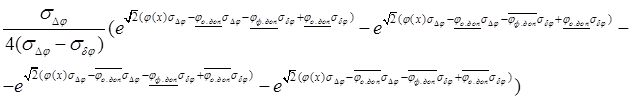
Таким образом, предложенный ранее в работах [3-5] метод количественной оценки риска, возникающего при моделировании с переменными, имеющими пороговые значения, распространен на случай моделей общего вида. Изучены случаи, в которых случайные ошибки, участвующие в анализе риска, имеют отличное от нормального распределения. Установлено, что предлагаемый метод подходит и для анализа таких ситуаций. Кроме того, показано, что при некоторых вариантах распределений ошибок возможно вычисление точного значения целевого интеграла. С другой стороны, естественно, имеются варианты, в которых необходимо использовать численные методы и с их помощью находить приблизительное значение риска.
Рецензенты:
Елохова И.В., д. э. н., профессор, заведующий кафедрой управления финансами Пермского национального исследовательского университета, г. Пермь.
Перский Ю.К., д.э.н., профессор кафедры менеджмента и маркетинга Пермского национального исследовательского университета, г. Пермь.