Краткосрочное прогнозирование суточных почасовых графиков электрической нагрузки является важной основой надежной и экономичной работы электроэнергетической системы. Точность прогноза электропотребления непосредственно влияет на качество диспетчерского управления и надежность электроснабжения. Таким образом, выбор подходящего метода прогнозирования нагрузки для повышения точности прогноза имеет важное практическое значение.
Учет фактора температуры воздуха при прогнозировании электропотребления реализован в различных моделях [1; 2]. Влияние температуры воздуха на электропотребление имеет более определенный характер, чем облачность и освещенность. Зависимости ЭП от освещенности имеют существенно более неопределенный характер. На рисунке 1 представлены примеры полученных зависимостей суточного ЭП от суточной интегральной освещенности для операционной зоны Ростовского РДУ в течение 2012 года. Коэффициенты детерминации как для линейной, так и нелинейной моделей свидетельствуют о слабых корреляционных связях. Разделение годовой выборки на сезоны года (рис. 2) приводит к повышению коэффициентов детерминации линейной и нелинейной моделей, причем, как это видно из рисунка, существенно увеличение коэффициента для нелинейной модели.
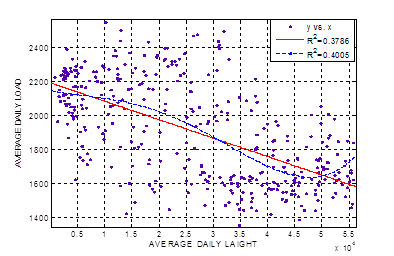
Рис. 1 – Зависимость суточного электропотребления от интегральной суточной освещенности на территории операционной зоны Ростовского РДУ в течение 2011 года
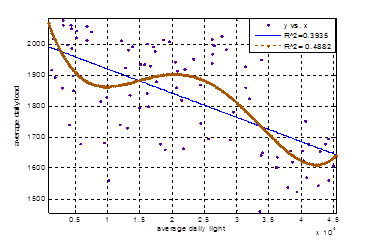
Рис. 2 – Зависимость суточного электропотребления от средней суточной освещенности на территории операционной зоны Ростовского РДУ в течение осени
Характер распределения точек суточного электропотребления в зависимости от освещенности показывает, что электропотребление имеет значительный разброс точек относительно кривых линейной и нелинейной регресии.
Вид зависимостей, представленных на рисунках 1, 2, показывает, что связь между электропотреблением и освещенностью имеет нелинейный характер, что указывает на необходимость использования математических моделей для прогнозирования методов электропотребления, которые позволяют учитывать нелинейный характер взаимосвязей электропотребления с влияющими на него факторами.
В статье приведены результаты моделирования и прогнозирования электропотребления на основе метода опорных векторов (SVM) [6; 7]. Метод опорных векторов представляет собой набор методов классификации и регрессии, который был разработан В.Н. Вапником в 1995 г. [7] и используется как для классификации, так и для построения регрессионных нелинейных моделей [4].
Модификация метода опорных векторов с использованием метода наименьших квадратов была впервые предложена J. Suykens [6] и является расширением стандартного метода SVM. В работе [5] метод LS SVM применен в задаче прогнозирования электрической нагрузки без учета метеофакторов (с учетом температуры воздуха). В [3] для прогнозирования суточных графиков электрической нагрузки метод опорных векторов применен в сочетании с генетическим алгоритмом и алгоритмом роя частиц. В данной работе указанный метод применяется для прогнозирования суточных часовых графиков электропотребления с учетом температуры воздуха и естественной освещенности.
Принцип минимизации цели в методе LS-SVM можно выразить как
(1)
Нелинейное выраженииe для модели прогнозирования будет иметь следующий вид:
, (2)
где 
- линейные коэффициенты, которые можно получить, решив уравнение (4); 
- ядро-функция, которая учитывает нелинейное отображение из входного пространства к высокой размерности пространства признаков; 
- ошибка, 
ошибки вектора; 
- вектор весов зазоров между кластерами (вектор коэффициентов разделения кластеров); С - параметр регуляризации, который контролирует ошибки; 
- множители Лагранжа; 
- ожидаемое значение прогнозируемой суммы, общее число точек известных данных; 
- нелинейное отображение входного пространства признаков в пространство более высокой размерности.
В качестве функции ядра часто используются следующие: линейные, полиномиальные, радиально-базисные, сигмовидные и Фурье-функции. Радиально-базисные функции имеют следующие преимущества: а) представления простых, даже для нескольких переменных входных; б) радиальная симметрия, гладкость, т.е. существуют производные любого порядка; в) функция простого разбора, и поэтому она облегчит теоретический анализ.
В данной статье в качестве функции ядра в регрессионной модели используется радиально-базисная функция следующего вида:
, (3)
где: 
- m-мерный входной вектор; 
- стандартизированный параметр, определяющий разброс функции вокруг центральной точки; 
- m-мерный вектор координат центра рассеяния; 
- норма вектора
, определяет расстояние между и . Радиальная базисная функция нелинейного преобразования обрабатывает нелинейные взаимосвязи между входной выборкой исходных данных в многомерном пространстве и выходной выборкой признаков в пространстве более высокой размерности. Коэффициент разброса (ширины) ядра отражает степень корреляции между обучающей выборкой входного пространства и вектором пространства признаков. При малых значениях ослабляются опорные векторы и усложняется процедура обучения (относительно сложные машины обучения), обобщающая способность не может быть гарантирована. При больших опорный вектор оказывает слишком сильное воздействие на регрессионную модель, и в результате трудно добиться достаточной точности прогнозирования.
Основные положения метода LS-SVM, применяемого для краткосрочного прогнозирования нагрузки [5; 6], изложены ниже.
Пусть обучающее множество задано как:
,
где 
- число измерений выбранных входных переменных.
Выбираются положительные числа и C , и соответствующая функция ядра
.
Далее решается задача оптимизации по методу множителей Лагранжа. Оптимальным решением будет вектор коэффициентов:
.
Построим функцию решения (формула (2)), где значения вектора коэффициентов 
рассчитываются по формуле:
. (4)
Выбор параметров и C в методе LS-SVM основывается на результатах опыта. В данной работе параметры функции ядра и параметры регуляризации выбираются как = 2，C = 30, соответственно. В работе [5] принимались значения = 7,27 и C = 9079,14.
В данной работе матрица входных данных содержит статистические данные суточных часовых графиков нагрузки, средней освещенности за сутки, типа дня, максимальной, минимальная и средней температуры воздуха за сутки. Выход представляет значение суточного часового графика нагрузки в день прогнозирования.
Выборка исходных за год разбивается на четыре выборки по сезонам года: весна, лето, осень, зима. Данные за 2009-2011 годы рассматривались как обучающая выборка.
Вследствие различия величин исходных данных они нормализуются.
Нормализация типа дня (рабочий день и выходной), с понедельника по пятницу (рабочие сутки), принимается как 1, суббота и воскресенье принимаются как 0.
Нормализация температурных данных выполняется по выражению:
, 
,
, (5)
где 
фактическая температура ℃；
,
, минимальная, максимальная температура; 
- нормализованная температура.
Нормализация данных освещенности выполняется аналогично:
, 
, 
, (6)
где 
- фактическая среднесуточная освещенность; 
,
- Минимальная и максимальная среднесуточная освещенности; 
нормированная среднесуточная освещенность.
Данные нагрузки нормализуются логарифмированием
, (7)
где 
- фактическая, а 
- нормализованная нагрузки в j-й час i-х суток. При нормализации данных с помощью линейных преобразований типа (5, 6) погрешность прогнозирования увеличивается.
Средой моделирования является MALAB2011a. Исходные данные взяты из статистических показателей по Ростовской области за период с 2009 по 2012 г., выходные данные представляют данные нагрузки на день прогнозирования. Результаты прогнозирования и фактическая нагрузка на одни сутки в разные сезоны года показаны на рис. 3. В таблице 1 приведены данные по погрешностям прогнозирования в виде средней абсолютной ошибки (MAPE) в процентах.
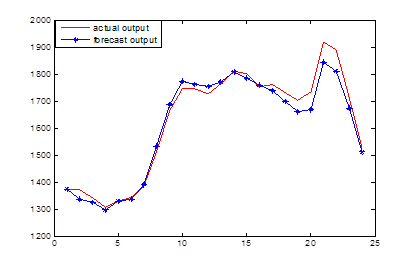
(а) лето 31/08/2011
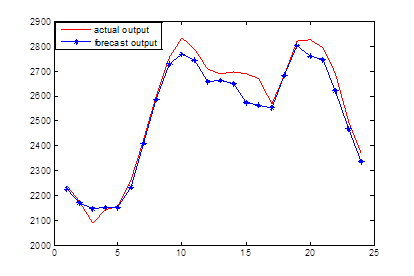
(б) зима 26/01/2012
Рис. 3 – Фактические и прогнозные графики нагрузки в различные сезоны года
Таблица 1. Погрешности прогнозирования суточных графиков нагрузки по модели LS-SVM для разных сезонов года при C = 30 , 
= 2
|
Время года |
Лето |
Зима |
Осень |
Весна |
|
Погрешность (MAPE), % |
1.4661 |
1.4541 |
1.1833 |
2.4341 |
|
Среднее значение погрешности (MAPE) 1.6344% |
||||
Как и следовало ожидать, наибольшие погрешности получены для весны и осени, так как в указанные сезоны года имеет место наибольшая динамика длительности светового дня и погодных факторов.
Следует отметить также, что ошибка прогноза в начале сезона больше, чем ошибка в конце сезона. Это связано с тем, что величины освещенности в начале сезона близки по величине к освещенности в конце прошедшего сезона, и величины освещенности в конце сезона близки к освещенности в начале следующего сезона.
Рецензенты:
Степанов В.П., д.т.н., профессор, заведующий кафедрой «Автоматизированные электроэнергетические системы» ФГБОУ ВПО «Самарский государственный технический университет», г. Самара.
Сычёв В.А., д. э. н., профессор, профессор кафедры «Производственный и инновационный менеджмент» ФГБОУ ВПО «Южно-Российский государственный политехнический универстет» (НПИ), г. Новочеркасск.