Введение
За последние десятилетия мировая робототехника и технологии, связанные с ними, развиваются стремительными темпами, приобретая все большую возможность использования мобильных роботов в различных областях человеческой деятельности. Для решения такого рода задач были разработаны несколько различных типов мобильных роботов, в том числе колесные роботы, гусеничные роботы, шагающие роботы, беспилотные летательные аппараты [1,7]. В данной работе рассматривается мобильный гусеничный робот, предназначенный для проведения поисковых операций. Выбор гусеничного движителя обусловлен рядом преимуществ, среди которых: маневренность, высокая проходимость, надежный контакт с поверхностью.
В данной статье представлен кинематический анализ движения мобильного гусеничного робота, оснащенного двумя независимыми гусеничными движителями.
Описание конструкции и принципа движения гусеничного робота
Конструкция гусеничного робота показана на рисунке 1.
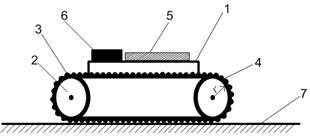
Рис 1. Схема гусеничного робота
Гусеничный робот состоит из следующих основных частей: 1 – корпус, 2 – ведущий каток, 3 – гусеница, 4 – ведомый каток, 5 – система автоматического управления электроприводами устройства, 6 – батареи питания, 7 – поверхность, по которой перемещается робот.
Робот перемещается за счет сил трения, возникающих между опорной поверхностью (грунтом) и гусеничным движителем робота. Ведущий каток соединен посредством редуктора с двигателем постоянного тока, управляемым системой автоматического регулирования. Проскальзывание между ведущими катками и гусеницей отсутствует, поэтому угловые скорости вращения катков (ведущих и ведомых) равны.
В зависимости от алгоритма перемещения и информации с датчиков система автоматического регулирования формирует управляющие напряжения для электроприводов устройства. Для усиления слаботочных сигналов с контроллера системы управления используются силовые транзисторные ключи – драйверы двигателей.
Для поворота в горизонтальной плоскости система управления формирует различное напряжение питания для каждого из гусеничных движителей. Система навигации робота может включать как ультразвуковые датчики расстояния, оптические линейки для перемещения по контрастной линии, так и контактные датчики препятствий.
Кинематический анализ движения мобильного гусеничного робота
Положение робота одназначано определяется координатами центра масс корпуса С и углом поворота корпуса φ. При кинематическом анализе движения гусеничного робота решается задача определения положения, скорости центра масс робота и скорости точек Сi, и Кi.
В рамках данного исследования были рассмотрены движения робота по окружности и спиралевидной траектории. Для получения численного результата при моделировании движения использовался пакет MathСad.
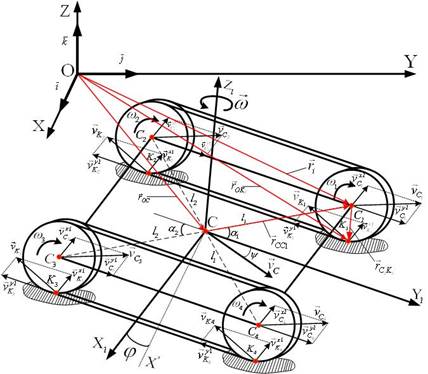
Рис 2. Расчетная схема гусеничного робота
На данной схеме приняты следующие обозначения: XOYZ – неподвижная система координат, CX1Y1Z1 – подвижная система координат, C1, C2, C3, C4 – точки крепления центров опорных катков; K1, K2, K3, K4 – точки контакта гусениц с поверхностью; 
– скорости точек крепления центра опорных катков; 
– проекции скоростей точек крепления центров опорных катков на ось CX1; 
– проекции скоростей точек крепления центра опорных катков на ось CY1; 
– скорости точек контакта опорных катков с поверхностью; 
– проекции скоростей точек контакта опорных катков с поверхностью на ось 
; 
– проекции скоростей точек контакта опорных катков с поверхностью на ось 
; ω1, ω2, ω3, ω4 – угловые скорости вращения опорных катков, l1 – расстояние от центра масс до 1-го и 4-го катка, l2 – расстояние от центра масс до 2-го и 3-го катка, φ – угол поворота корпуса робота вокруг CZ1. 
– угол между линией CC1 и осью CY1 (
для i=1,4; 
для i=2,3 соответственно).
Определим радиус-вектор, описывающий движение корпуса робота в неподвижной системе координат:
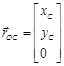, где 
и 
– проекции радиус вектора в абсолютной системе координат.
Для определения скорости центра масс продифференцируем следующее выражение:
.
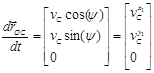При этом скорость центра масс в системе координат 
будет иметь вид:
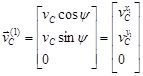, а в системе координат
:
.
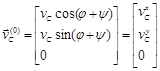Угловая скорость корпуса робота 
определяется следующим образом:
Определим радиус-вектор точек закрепления катков гусеничного робота как: 
Скорости для этих точек могут быть получены как:
или 
;
;
Аналогичным образом можем записать для точек контакта с поверхностью:
; 
; 
;
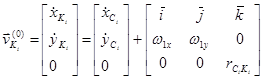
где 
– скорость точек 
в абсолютной системе координат.
, 
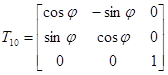
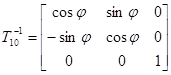где 
– скорость точек 
в относительной системе координат.
Положение точек центров катков робота задается следующими проекциями:
; 
;
; 
;
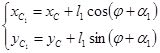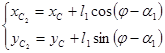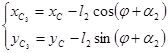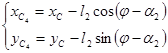где, 
– координаты центра 
-того катка ( 
), – координаты центра масс гусеничного робота.
Пусть центр масс корпуса робота движется по окружности, координаты которого задаются уравнениями: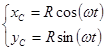 
, где R – радиус кривизны окружности, по которому движется центр масс робота,
– угловая скорость корпуса робота. Будем считать, что когда 
, подвижная ось CY1 всегда направлена по касательной к траектории, и угол φ изменяется по заданному закону, то есть 
, где 
– начальный угол, определяющий положение корпуса робота на траектории.
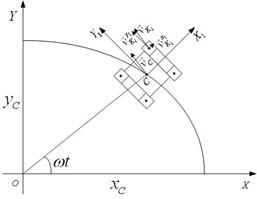
Рис 3. Схема движения робота по траектории
Проведем моделирование движения робота и определим траекторию. Результаты моделирования представлены на рис. 4–5.
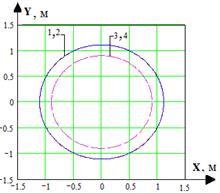
Рис. 4. Траектория движения робота при движении
по окружности: 1, 2 – скорости катков забегающей гусеницы; 3, 4 – скорости катков отстающей гусеницы
а)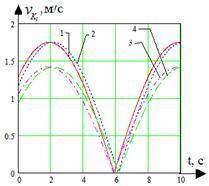
б)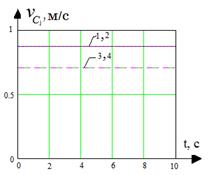 
Рис 5. Временные диаграммы параметров движения робота по окружности 1, 2 – скорости катков забегающей гусеницы; 3, 4 – скорости катков отстающей гусеницы; а – зависимость скорости точек контакта робота с поверхностью от времени; б – зависимость скорости точек центров катков робота от времени
Отметим, что при движении по криволинейной траектории в точке контакта опорных катков с поверхностью возникает продольное проскальзывание. Для оценки величины проскальзывания осуществим моделирование движения гусеничного робота по спиралевидной траектории, при которой радиус окружности будет изменяться во времени, т.е. R = R(t).
В данном случае, координаты центра масс будут задаваться уравнениями:
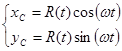
Выполним численный расчет движения робота в MathCAD и получим график траектории движения робота. Также, построим графики зависимости скоростей точек контакта с поверхностью от времени. Результаты моделирования представлены на рис. 6–7.
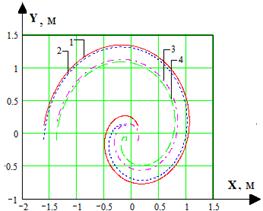
Рис. 6. Траектория движения катков робота при спиральном движении:
1, 2 – скорости катков забегающей гусеницы; 3, 4 – скорости катков отстающей гусеницы
а)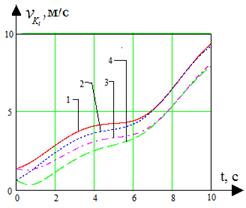
б)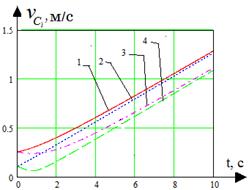
Рис 7. Временные диаграммы параметров спирального движения робота: 1, 2 – скорости катков забегающей гусеницы; 3, 4 – скорости катков отстающей гусеницы; а – зависимость скорости точек контакта робота с поверхностью от времени; б – зависимость скорости точек центров катков робота от времени
Определим величину продольного скольжения катков робота. Для этого вычислим нормальную составляющую скорости каждого катка, воспользовавшись формулой:
Произведя необходимые вычисление в MathСad, получим графики проскальзывания каждого из катков робота.
а)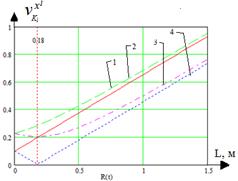
б)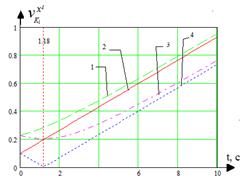
Рис. 8. Зависимость проскальзывания от радиуса кривизны:
1, 2 – скорости катков забегающей гусеницы; 3, 4 – скорости катков отстающей гусеницы
Как видно из графика, величина продольного проскальзывания нелинейно зависит от радиуса кривизны криволинейной траектории. Характерной является точка, обозначенная на рис. 8, где R=0,18 м, а t=1,18 с. В данном случае скорость второго опорного катка робота, являющегося ведомым во внешней гусеничной паре, становится равной нулю. По сути, в этот момент времени робот начинает вращаться относительно этого катка. После этого момента, когда R>0,18 м, скорость всех катков имеет вид возрастающей прямой, так как радиус кривизны линейно изменяется во времени.
Заключение
В данной работе проведен анализ кинематики движения гусеничного мобильного робота, определены основные закономерности его движения при заданном радиусе кривизны траектории, полученные результаты в дальнейшем будут использоваться при изучении динамики движения робота, в частности, величина проскальзывания и скорость вдоль оси CY1 будут учитываться при определении сил сухого трения, действующих в точках контакта робота с поверхностью.
Рецензенты:
Савин Л.А., д.т.н., профессор, заведующий кафедрой «Мехатроника и МИ», ФГОУ ВПО «Госуниверситет УНПК», г. Орел.
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск.