Введение
При исследовании популяций, развивающихся в пространстве и времени, возникает задача оценки численности популяции в произвольных областях в некоторый момент времени, зная начальное распределение [1]. Под однотипной популяцией в данной работе рассматривается популяция бактерий. Предполагается, что наблюдается не вся область, а лишь выборочные ее сектора в случайные моменты времени. При этом наблюдение сильно зашумлено – в момент подсчета числа бактерий в некоторой области бактерии могут перемещаться в соседние области. По этой причине разработка алгоритмов и математических моделей, предназначенных для анализа роста однотипных популяций, представляет актуальную научную проблему. Целью данной работы является построение адекватной математической модели, позволяющей анализировать развитие однотипной популяции в пространстве и времени. Методом исследования является имитационное стохастическое моделирование. Оценка реального числа бактерий в секторе на основе наблюдений осуществляется с помощью дискретной схемы Калмана.
Описание модели
Рассмотрим математическую модель роста однотипной популяции, развивающуюся из исходной популяции во времени и двумерном пространстве. Для определенности опишем процесс, являющийся моделью роста популяций бактерий.
Предположим, что ареал 
имеет форму прямоугольника. Разобьем ареал на одинаковые прямоугольные области
, 
и 
,
и
– натуральные числа, таким образом 
, и .
В каждой области 
, и может находиться неотрицательное целое число бактерий. Каждая бактерия может с вероятностью 
(
) поделиться на две. Обозначим 
процесс, считающий количество появившихся бактерий в результате деления внутри области ( и ). Предполагается, что интенсивность деления пропорциональна количеству бактерий в области в момент времени 
с коэффициентом пропорциональности , т.е. компенсатор процесса описывается классической моделью Мальтуса [3] и равен:
(1)
где 
– количество бактерий в момент времени t внутри области ( и ). Основные определения и термины для описания семи мартингалов см. в [2].
Рассмотрим также процессы перехода бактерий в область из соседних областей и ухода бактерии из области в соседние области. Обозначим их 
и 
( и ) соответственно. Предполагается, что компенсатор процесса ухода бактерии из области ( и ) также пропорционален количеству бактерий в области в момент времени с коэффициентом пропорциональности 
.
, (2)
где – интенсивность ухода бактерии из области из области ( и ).
а) 
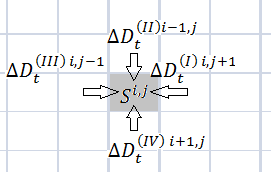б)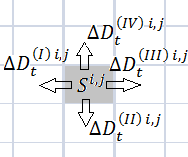 
Рисунок 1. Переходы бактерий из области и в область из соседних областей
Обозначим 
– количество бактерий, перешедших из области в область 
, и 
в момент времени ; 
– из области в область 
, 
и ; 
– из области в область 
, и 
и 
– из области в область , и , см. рисунок 1 (а, б). Пусть бактерии не умирают, тогда выполняется соотношение:
(3)
Предполагается, что бактерия не может одновременно перейти в две разных области, т. е. выполняется равенство (4).
P-п. н. (4)
Предположим, что переходы бактерий из области будут происходить в момент скачков пуассоновского процесса
. Обозначим эти моменты 
, 
, и . Тогда вероятности переходов будут равны:
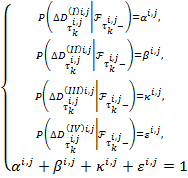(5)
С учетом (5) процесс равен
(6)
Предположим, что ареал замкнут всюду, т. е. 
; 
; 
и 
.
С учетом формул (1-3, 6) получаем, что количество бактерий в области ( и ) в момент времени t равно
(7)
где 
– начальное количество бактерий в из области ( и ).
Процесс наблюдения 
за процессом будет выглядеть следующим образом
, 
(8)
, ,
где 
– целочисленная случайная величина, распределенная по закону Пуассона с параметром 
, ошибка измерений.
Предположим, что распределение бактерий в начальный момент времени по областям ареала неравномерно. Требуется по наблюдению оценить численность бактерий в каждой области ареала.
Теоретическая оценка математического ожидания числа бактерий
Математическое ожидание процесса , считающего количество бактерий в области ( и ), из уравнений (1, 2, 6, 7) равно:
, (9)
где и , причем слагаемые с индексами: 0, 
и 
равны 0. Запишем полученные уравнения (9) в дифференциальном виде:
(10)
Получена система 
однородных линейных дифференциальных уравнений (10) с 
неизвестными и начальными значениями . Решение таких систем подробно изложено в [4]. Решение в общем виде можно записать через матричную экспоненту:
(11)
где 
– вектор, 
; 
– матрица, составленная из коэффициентов уравнений (10); 
– начальное значение вектора
.
Оценка численности числа бактерий
Предположим, что наблюдение за областями 
и происходит в случайные моменты времени 
, 
скачков пуассоновского процесса 
с интенсивностью 
одновременно во всех областях . И предположим также, что при подсчете количества бактерий в области и происходит ошибка 
, т. е.
(11)
где , – совокупность независимых случайных величин, c нулевым средним и дисперсией 
.
Значение процесса
в моменты времени будет отличаться от математического ожидания 
на некоторую мартингальную часть. В предыдущем пункте был рассмотрен способ, позволяющий отыскать теоретическую оценку математического ожидания числа бактерий. Само решение зависит от конкретных значений интенсивностей переходов и 
и весовых коэффициентов
, 
, 
, 
, , , поэтому обозначим, что от момента до момента 
математическое ожидание числа бактерий меняется по закону:
(12)
где 
– некоторая функция, которая ищется исходя из решений уравнений (10). Суммируя вышесказанное, получаем формулу (13):
, (13)
где 
– независимые одинаково распределенные случайные величины с нулевым средним и дисперсией 
.
Рассмотрим способ оценки реального числа бактерий 
по наблюдению за областью и на основе дискретной схемы Калмана [5].
В каждый момент времени оценка реального числа бактерий в области будет считаться как средневзвешенное между теоретической оценкой бактерий и наблюдаемыми значениями с коэффициентами 
и 
соответственно, где 
– коэффициенты Калмана [5].
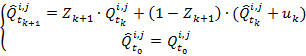(14)
где – коэффициент Калмана, 
. Нужно так подобрать коэффициенты
, чтобы получившаяся оценка числа бактерий 
была наиболее близкой к реальному числу 
. К примеру, если известно, что ошибка обнаружения при подсчете числа бактерий очень мала, то коэффициенту нужно придать больший вес. И наоборот, если известно, что значение числа бактерий при подсчете очень не точное, следует больше ориентироваться на теоретически предсказанное значение 
.
Если обозначить ошибку 
между реальным значением числа бактерий в области и их оценкой , тогда задачу оценивания можно переформулировать в задачу минимизации среднеквадратической ошибки в момент времени , см. формулу (16).
(15)
(16)
Теорема. При сделанных выше предположениях оценка числа бактерий будет оптимальной при:
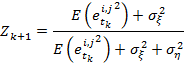
Доказательство
Используя уравнения (11), (13) и (14), перепишем уравнение (15) в виде:
Из предположения независимости случайных величин, входящих в 
и с учетом того, что 
и 
получаем, что выражение (15) можно переписать в виде:
Это выражение принимает минимальное значение при
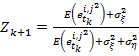(17)
Среднеквадратичная ошибка, минимизирующая значения коэффициентов Калмана, при этом равна:
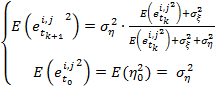(18)
Что и требовалось доказать.
Заключение
Рассмотренная в статье модель позволяет описать рост однотипной популяции в пространстве и времени на основе семимартингальных точечных процессов по известному начальному распределению. Получена итерационная формула (17) для вычисления оптимальной оценки числа бактерий в произвольной области на основе нескольких наблюдений.
Работа выполнена при поддержке Министерства образования и науки РФ (НИР, проводимые в рамках государственного задания Министерства образования и науки РФ на 2013 г., Программы стратегического развития УлГУ на 2012–2016 гг., Программы развития деятельности студенческих объединений УлГУ на 2012-2013 гг.).
Рецензенты:
Кемер А.Р., д.ф.-м.н., профессор, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.
Андреев А.С., д.ф.-м.н., профессор, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.