Введение
Нахождение оптимального месторасположения объекта производственной цепи является важным процессом, так как от этого зависят затраты на размещение, возможная прибыль, доступность предприятия для клиентов и поставщиков. Для решения данной задачи существуют различные методы и технологии [2]: математические, эвристические, геоинформационные. Эвристические методы позволяют рассматривать различные критерии оптимизации размещения. По сравнению с ними наибольшую точность в получении конечных результатов можно ожидать от математических методов, а наглядность решения – от геоинформационных технологий [3]. Наиболее распространенными методами являются: решение задачи охвата и единого среднего, определение центра тяжести, имитационное моделирование. Эвристические методы обычно применяют на предварительном этапе для оценки возможных мест размещения. В их поддержку геоинформационные технологии позволяют оценить полученный результат с помощью инструментов пространственного анализа. Существующие методы не обладают достаточной степенью универсальности и не гарантируют в полной мере оптимальность решения.
Методика нахождения оптимального решения задачи о размещении
Для повышения универсальности имеющихся методов предлагается использование предлагаемой методики, которая объединяет возможности нескольких методов для получения наиболее оптимального решения. Она основывается на решении оптимизационной задачи.
Методика включает в себя следующие этапы решения задачи:
1. Нахождение решения задачи о размещении с применением известных математических методов. Расчет показателей эффективности размещения: затрат, прибыли.
2. Построение на основе метода наименьших квадратов целевой функции затрат или прибыли посредством аппроксимации полученных решений на предыдущем этапе [1]. После получения уравнения проводится его оценка с помощью различных критериев: средняя ошибка аппроксимации, критерий детерминации.
3. Формирование ограничений задачи оптимизации. Для этого определяется градиент целевой функции в различных точках области размещения объекта. Определяется шаг градиента в сторону максимума целевой функции и отмечается точка границы возможного размещения объекта. Количество таких точек определяет число ограничений. Построение функций ограничений определяет область допустимых решений задачи.
4. Поиск оптимального места размещения объекта.
Реализация методики на примере
В республике Хакасия наиболее приоритетным направлением развития является создание Абакано-Черногорской агломерации. В ходе реализации проекта планируется на территории сформировать пять производственных кластеров: строительно-индустриальный, агропромышленный, машиностроительный, топливно-энергетический, транспортно-логистический. На этапе проектирования будущей агломерации важно решение задачи о размещении производственных объектов, что позволит создать эффективную сеть взаимосвязанных кластеров.
Рассмотрим задачу о размещении объекта строительно-индустриального кластера. Пусть необходимо определить месторасположение некоторого производственного объекта. Имеются данные о существующих и потенциальных клиентах, объемах потребления товаров или услуг, координаты их расположения на географической территории.
Первоначально находят места размещения объекта с помощью нескольких методов: решение задачи единого среднего и задачи охвата, определение центра тяжести и имитационного моделирования [4,5]. Используя данные методы, полученные решения представлены в таблице 1. Каждый метод дал по одному решению, за исключением имитационного моделирования, в результате использования которого определено два возможных места размещения.
Для упрощения расчетов можно воспользоваться программой для ЭВМ «Программа решения задачи размещения предприятий». Подробнее ее использование рассмотрено в работе [6].
Таблица 1. Возможные места размещения производственного объекта
|
№ п/п |
Координата x о в. д. (восточной долготы) |
Координата у, о с. ш. (северной широты) |
Значение издержек на размещение (Zi), руб. |
|
1 |
91.341346 |
53.766951 |
75177 |
|
2 |
91.401774 |
53.754743 |
95489 |
|
3 |
91.376035 |
53.706837 |
123606 |
|
4 |
91.339262 |
53.768529 |
75680 |
|
5 |
91.470524 |
53.669068 |
121653 |
Для каждого решения рассчитываются затраты на размещение по формуле:
, (1)
где 
– стоимость аренды в зависимости от географического расположения; 
– стоимость транспортных расходов, которые вычисляются по формуле (2), i = 1,2,…, n – порядковый номер возможного места размещения объекта (в данном примере n = 5).
, (2)
где 
– сумма расстояний (длин) от каждого клиента j до места размещения объекта; 
– транспортный тариф, j = 1,2,…, m – порядковый номер клиента.
Далее на основе метода наименьших квадратов строится целевая функция издержек путем аппроксимации ранее полученных координат мест размещений. В качестве возможного вида уравнения было выбрано:
. (3)
Для (3) вычисляются значения коэффициентов ai, при которых функция должна иметь минимум: 
Известно, что в точке минимума первая производная (3) должна быть равна нулю:
, (4)
что позволяет определить ai через систему уравнений:
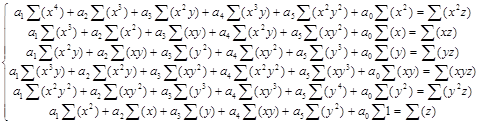(5)
В (5) заносятся исходные значения x и у. В итоге получаем систему уравнений с 6-ю неизвестными.
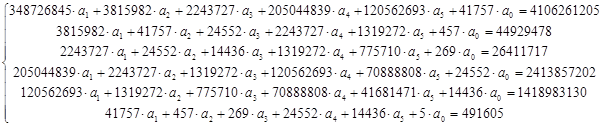
Решая данную систему уравнений методом Гаусса, определяются значения коэффициентов: a0=55661.742, a1=2020.913, a2=330194.646, a3=128042.515, a4=-14310.032, a5=5672.763.
Тогда уравнение (3) примет вид:
(6)
Необходимо определить, насколько уравнение (6) адекватно описывает имеющуюся зависимость. Для этого можно воспользоваться следующими показателями: средняя ошибка аппроксимации и коэффициент детерминации [7]. Средняя ошибка аппроксимации должна быть в интервале 8–10 %, тогда полученное уравнение считается адекватным. Она рассчитывается по формуле:
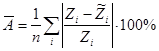, (7)
где 
– исходные значения затрат по каждому i-му месту размещения, 
– значения затрат, полученные по уравнению (6).
Для рассматриваемого примера средняя ошибка аппроксимации составила 8,4 %.
Коэффициент детерминации отражает, насколько исходные данные могут быть объяснены полученной моделью. Он измеряется в интервале от 0 до 1, чем полученное значение ближе к единице, тем уравнение объясняет большую часть изменчивости соответствующих переменных. Коэффициент находится по формуле:
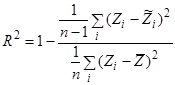(8)
где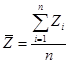 
– среднее значение исходных затрат.
Значение критерия детерминации для примера получилось равным 0,7.
Рассчитанные по (7) и (8) показатели подтверждают значимость уравнения (6), которое можно использовать в качестве целевой функции затрат для дальнейшего решения задачи о размещении.
Далее строятся ограничения, накладываемые на поиск оптимума задачи. Для каждого полученного ранее решения определяется градиент, указывающий на направление наискорейшего возрастания целевой функции, значение которой меняется от одной точки пространства к другой. Он определяется по формуле:
(9)
Все рассчитанные значения градиентов оказались отрицательными, что свидетельствует о нахождении антиградиента, показывающего направление наискорейшего убывания функции.
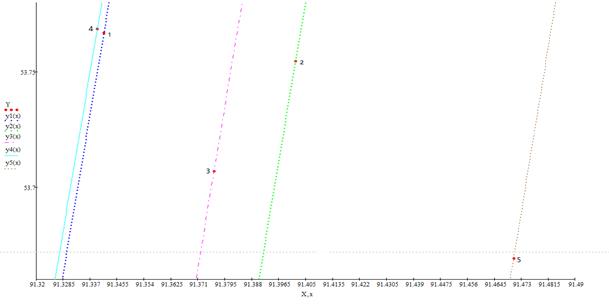
Рисунок 1. Антиградиенты целевой функции в точках опорного решения
В направлении снижения уровня затрат найдем точки в пределах территории, отведенной для размещения объекта. Совокупность точек начального решения и точек с наименьшими затратами будет составлять область допустимых значений (рис. 2).
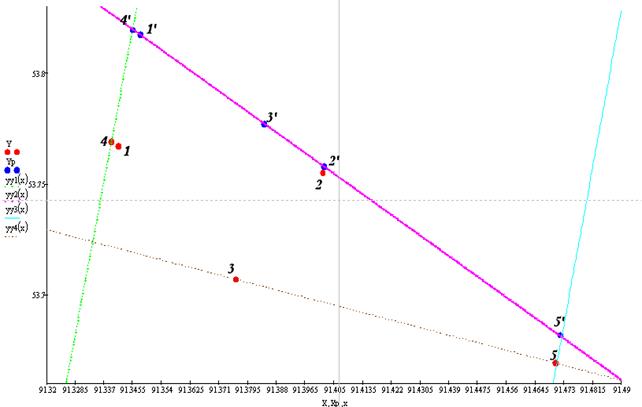
Рисунок 2. Область допустимых значений
В результате имеем следующую задачу минимизации:
при ограничениях
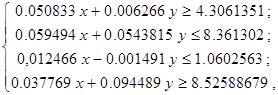
при 
.
Получили следующее решение x=91.345555ов.д., y=53.8195812ос.ш.. Затраты на размещение составят 51930 рублей. Эти координаты определяют наилучшее расположение предприятия с наименьшими затратами.
Заключение
Разработанная методика позволяет найти оптимальное решение задачи о размещении. Она обладает достаточной универсальностью и позволяет учесть несколько предварительных решений в получении координат возможного размещения объекта. Недостаток методики заключается в её сложности, использование которой состоит в следующем: если требуется для нескольких объектов найти места их размещения, то по каждому из них следует предварительно применить несколько методов (каждый из которых позволяет использовать только ему присущие возможности в определении координат).
Рецензенты:
Кочетков В.П., д.т.н., профессор, профессор кафедры «Электроэнергетики» Хакасского технического института – филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан.
Нагрузова Л.П., д.т.н., доцент, профессор кафедры «Строительство» Хакасского технического института – филиала ФГАОУ ВПО «Сибирский федеральный университет», г. Абакан.