Введение
Проведенный нами анализ математической и информационно-технологической подготовки курсантов военных учебных заведений показал, что в числе методических проблем, возникающих в процессе обучения высшей математике и информатике, является нарушение преемственности между школой (в частности, в кадетских классах) и высшим военным образовательным учреждением; существует серьезный отрыв предметных знаний от практики, влекущий за собой непонимание роли указанных дисциплин в их дальнейшей учебно-профессиональной и профессиональной деятельности. Это негативно сказывается на качестве математической и информационно-технологической подготовки будущих военных специалистов, прежде всего, в аспекте установления межпредметных связей между элементами изучаемого предметного содержания с целью обучения поиску пути решения задач, имеющих место в военно-инженерной практике.
1. Основная часть
1.1. Этапы решения военно-прикладных задач помощью программных средств образовательного назначения
В качестве основного направления решения данной проблемы, на наш взгляд, может рассматриваться организация интегрированного элективного курса прикладного характера в кадетских классах. Практическая и прикладная направленность такого курса обеспечивается систематическим применением математического аппарата для решения задач военно-прикладного характера с помощью современных программных средств образовательного назначения.
На основе интегрирования классического подхода, принятого в теории и методике обучения решению математических задач (Д. Пойа, Ю.М. Колягин, И.В. Крупич, Г.И. Саранцев и др.) [4, 5, 6 и др.], и известной схемы решения задачи с помощью компьютера [1, 2, 7 и др.] мы выделяем следующие этапы решения военно-специальных задач с помощью программных средств образовательного назначения (рис.1):
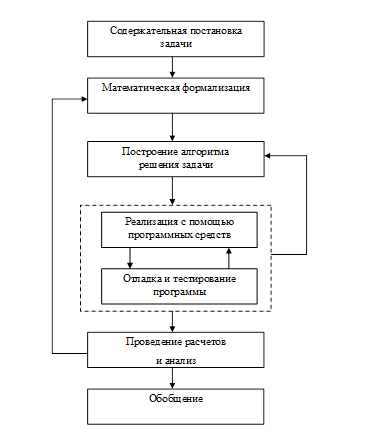
Рисунок 1. Этапы решения военно-специальных задач помощью программных средств образовательного назначения для кадетских классов
1. Содержательная постановка задачи.
На этом этапе целесообразно построить специальную динамическую схему - рисунок на дисплее, который во многих случаях поможет восстановить ситуацию, возникающую в военной практике, и, соответственно, облегчит понимание условия задачи и поиск ее решения. Здесь же выделяем с кадетами известные и неизвестные величины, рассматривая их не только в сугубо предметном, но и в военно-прикладном аспекте (попутно актуализируя сведения из специальных дисциплин), а также «прикидываем» возможный ответ.
2. Математическая формализация.
Главная цель работы учителя на данном этапе - с помощью системы целесообразных вопросов и «наводок» подтолкнуть кадетов к идее решения. Отправной точкой для этой работы является, как правило, либо определенное видоизменение задачи с целью ее отнесения к известному типу задач, либо пошаговое выделение базовых формул или утверждений, отражающее аналитико-синтетический путь рассуждений от требования к условию и обратно. Следует отметить, что процесс поиска плана решения должен сопровождаться по возможности адекватным преобразованием исходного рисунка или схемы.
Далее строим с кадетами математическую модель (система математических соотношений - формул, уравнений, неравенств и т. д., отражающих существенные свойства объекта или явления). Выделяем в явном виде предположения, на которых будет основываться математическая модель; фиксируем математические соотношения, связывающие результаты с исходными данными. Для корректной интерпретации этих соотношений используются «системообразующие» вопросы, которые задает учитель.
3. Построение алгоритма решения данной задачи.
На этом этапе происходит разработка алгоритма, которая включает в себя выбор метода проектирования алгоритма; выбор формы записи алгоритма (блок-схемы, псевдокод и др.); проектирование самого алгоритма. Обговаривая в группе все соотношения и осознавая при этом наличие и характер связей между понятиями и комплексами понятий, соответствующими тому или иному блоку, кадеты смогут относительно самостоятельно перейти к построению алгоритма решения данной задачи и его проверке на конкретных числовых данных.
4. Реализация решения задачи с помощью программных средств образовательного назначения.
Здесь рассматриваем возможные варианты решения данной задачи на компьютере и без него. Предлагается кадетам реализовать решение задачи различными способами (средствами Excel, Mathcad, языки программирования и т.д.). Последующее «прикидочное» сопоставление предлагаемых подходов по различным параметрам дает возможность выбора наиболее оптимального в данной конкретной ситуации подхода.
5. Отладка и тестирование программы.
Тестирование и отладка включают в себя синтаксическую отладку; отладку семантики и логической структуры программы; тестовые расчеты и анализ результатов тестирования; а также поиск пути совершенствования программы.
6. Проведение расчетов, анализ и проверка полученных результатов.
Это использование уже разработанной программы для получения искомых результатов. Необходимо сравнить то, что требовалось найти, с тем, что фактически найдено. До конца ли выполнена задача? Насколько правдоподобен полученный результат? На этом этапе производится анализ результатов решения задачи и в случае необходимости - уточнение математической модели (с последующей корректировкой алгоритма и программы).
7. Обобщение. На этом этапе происходит анализ различных способов решения поставленной задачи, использованных кадетами, выбор эффективного метода реализации решения задачи с помощью программных средств образовательного назначения, исследование решения, а также поиск возможных направлений развития данной задачной темы.
1.2. Реализация методики обучения работы с военно-прикладной задачей
Реализуем выделенную последовательность этапов работы над задачей на примере темы «Законы распределения случайных величин» в рамках разработанного нами интегрированного элективного курса для кадетских классов.
Задача. По цели производится три независимых выстрела. Вероятность попадания в цель при каждом выстреле 0,4. Построить ряд распределения и функцию распределения числа попаданий в цель.
(1). Понимание и постановка задачи.
В рамках этого этапа целесообразно рассказать кадетам, что такое артиллерийский выстрел.
Затем возвращаемся к условию задачи и выделяем с кадетами известные и неизвестные величины, записываем условие задачи.
(2). Математическая формализация.
Переходим к анализу и поиску пути решения задачи, которые будем проводить в вопросно–ответной форме. Затем строим с кадетами математическую модель. Записываем математические формулы, которые связывают известные и неизвестные величины.
(3). Построение алгоритма решения данной задачи. На данном этапе выбираем форму алгоритма решения данной задачи. Предлагаем кадетам составить блок-схему решения данной задачи. Здесь необходимо вспомнить с кадетами понятие блок-схемы и ее основные элементы. После чего кадеты могут приступить к составлению алгоритма решения данной задачи (рис.2).
(4). Решение задачи на ЭВМ. Обсуждаем и реализуем с кадетами возможные варианты решения данной задачи с помощью программных средств образовательного назначения, а именно: средствами MS Excel, Mathcad, языки программирования и т.д.
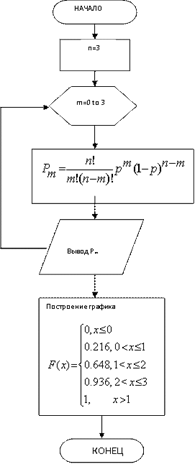
Рисунок 2. Алгоритм решения задачи
(5). Отладка и тестирование программы. Тестирование и отладка включают в себя синтаксическую отладку; отладку семантики и логической структуры программы; тестовые расчеты и анализ результатов тестирования; совершенствование программы. Например, реализуя решение задачи средствами MathCad, кадеты особое внимание уделяют отладки построения функции распределения (указывают направление осей, подбирают правильный интервал для построения графика).
(6). Проведение расчетов и анализ полученных результатов.
На данном этапе идет проверка правильности решения задачи, анализ полученных результатов. Мы выясняем, всегда ли задача имеет решение и сколько решений может иметь задача. Для этого нужно рассмотреть все шаги построения, всегда ли они выполнимы и сколько дают результатов.
(7). Обобщение.
Учитель вместе кадетами обсуждает, какое программное средство является наиболее эффективным для решения поставленной задачи. В данном случае приходим к выводу, что решение данной задачи эффективнее реализовать с помощью MathCad. Технология работы в средах Microsoft Excel и MathCad в данном случае имеет преимущество перед языками программирования. Отладочные фрагменты можно оставить в готовой таблице или в MathCad-документе для того, чтобы убедиться в правильности хода решения на определенном этапе решения задачи. Математические выражения в MathCad представляются в общепринятой математической нотации, то есть, имеют точно такой же вид, как в книге, тетради, на доске.
Заключение
В целом можно констатировать, что эффективность работы по подготовке будущих военных специалистов к обучению в военных вузах во многом зависит от следующих условий: с одной стороны, рассматриваемый учебный материал должен быть связан с будущей профессиональной деятельностью кадетов, в частности, базироваться на знаниях специальных дисциплин, на постоянном применении математических знаний и навыков работы с программными образовательными продуктами для решения задач, имеющих место в военной практике, а с другой - само содержание и структура этого материала должны позволить кадету любого уровня общеобразовательной и специальной подготовки активно включаться в учебно-познавательный процесс и максимально проявить себя в нем.
Рецензенты:
Найниш Л.А., д.п.н., профессор, заведующий кафедрой начертательной геометрии и графики, Пензенский государственный университет архитектуры и строительства Министерства образования и науки РФ.
Мещеряков А.С., д.п.н., профессор, Пензенский государственный университет Министерства образования и науки РФ.



