Введение

В настоящее время в отечественной и зарубежной практике для расчета железобетонных изгибаемых элементов применяется модель пластического шарнира. Данная модель очень проста в вычислении, однако имеет ряд недостатков, не позволяющих проследить ни за развитием напряжений или деформаций по поперечному сечению на всех стадиях нагружения балки, ни за порядком потери несущей способности композитных материалов (арматуры и бетона). Потеря несущей способности балки может возникать вследствие разных причин и при любой стадии напряженно-деформированного состояния сечения. Для полного исследования работы железобетонного элемента недостаточно расчета только по третьей стадии НДС (как это происходит при расчете по методу пластического шарнира). Железобетонная балка в большинстве случаев разрушается вследствие либо текучести арматуры, либо разрушения крайнего сжатого фибра бетона. Одновременное достижение этих предельных состояний является лишь частным случаем разрушения сечения и происходит редко. Тут большую роль играют многие параметры, такие как высота поперечного сечения балки, рабочая высота поперечного сечения балки, ширина сечения балки, прочность бетона и арматуры, начальный модуль упругости бетона и арматуры, площадь сечения арматуры и др.

В данной статье рассматривается деформационная модель сечения, использующая другие принципы расчета изгибаемых железобетонных элементов. Новая методика позволяет проследить за нелинейным изменением напряженно-деформированного состояния сечения железобетонных балок от начала их загружения до момента разрушения, а также определить момент потери несущей способности бетона и арматуры.

Цель исследования

Целью исследования является разработка новой нелинейной модели расчета железобетонных балок.

Материал и методы исследования

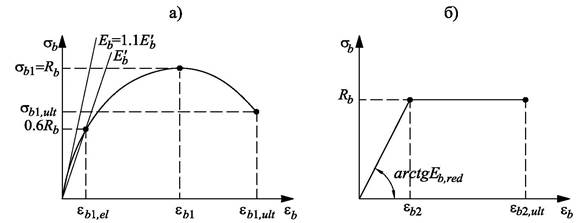
Рис. 1. Зависимости «напряжение-деформация» сжатой зоны бетона: а) общая диаграмма с ниспадающей ветвью; б) диаграмма Прандтля.

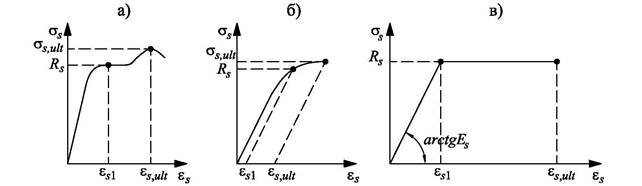
Рис. 2. Зависимости «напряжение-деформация» растянутой арматуры: а) диаграмма с физическим пределом текучести; б) диаграмма с условным пределом текучести; в) диаграмма Прандтля.

Новая модель расчета, основанная на гипотезах и предпосылках евростандартов [6], строится на основе нелинейных деформационных зависимостей бетона и арматуры, представленных в виде диаграмм (рис. 1 и 2).

Ниже представлен расчет прямоугольного поперечного сечения железобетонной балки, с использованием в качестве зависимостей «напряжения-деформации» диаграммы Прандтля для бетона и арматуры (рис. 1б и 2в).

Сперва рассмотрим возможные случаи потери несущей способности железобетонной балки (рис. 3):

I случай: , (); (1)

II случай: , (); (2)

III случай: ,(). (3)

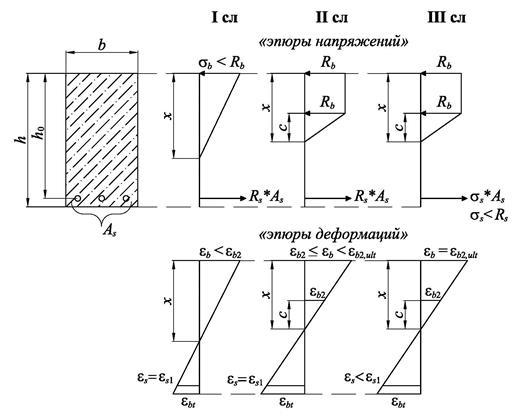
Рис. 3. Поперечное сечение и случаи потери несущей способности железобетонной балки.

Соответственно для каждого случая составляются уравнения равновесия продольных сил N:

Для I случая: , (4)

где .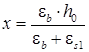

Для II случая: , (5)

где , .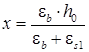

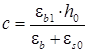Для III случая: , (6)

где , .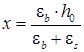

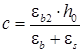Для I и II случаев в качестве неизвестной переменной выступает , а для III - . Определив их значения, проверим, удовлетворяют ли эти переменные условиям (1), (2) и (3). В случае сходимости с данными условиями переходим к определению изгибающего момента М:

Для I случая: 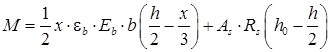; (7)

Для II случая: 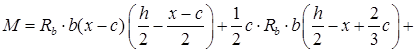(8)

;

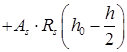Для III случая: 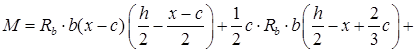(9)

.

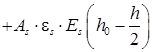Результаты и выводы исследования

В таблице 2 представлен сравнительный анализ расчетных значений деформационной модели и модели пластического шарнира со значениями опытных балок, испытанных в НИИЖБ [5]. Характеристики этих балок представлены в таблице 1.

Таблица 1 – Характеристики опытных балок.

Таблица 2 - Сравнение изгибающих моментов и расположений нейтральных слоёв при расчетах по деформационной модели сечения и модели пластического шарнира со значениями опытных балок.

Из представленных результатов видно, что изгибающие моменты Мр и высоты сжатых зон бетона xр, полученные в результате расчета по деформационной модели сечения, наиболее приближены к значениям Моп и xоп опытных балок по сравнению с Мш и xш пластического шарнира. Отсюда следует, что деформационная модель сечения экономически и практически более целесообразна для применения в расчетах железобетонных балок, чем модель пластического шарнира.

Рецензенты:

Глухих В.Н., д.т.н., профессор, заведующий кафедрой «Техническая механика», ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.

Веселов А.А., д.т.н., профессор кафедры «Железобетонные и каменные конструкции», ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.