Введение
В статистической отчетности Росстата [5] имеются различные макроэкономические индикаторы, отражающие социально-экономическое состояние как РФ в целом, так и отдельных ее субъектов (федеральных округов, ФО). Эти индикаторы получены в результате статистической обработки соответствующих эмпирических выборок, причем в качестве центральной тенденции эмпирического распределения используются средние арифметические значения за определенный временной период (в Росстате это именуется «в среднем за период» [5]). При выполнении анализа социально-экономического состояния РФ и отдельных ее субъектов проводится сравнение средних арифметических значений макроэкономических индикаторов для одного временного периода по различным качественным критериям (регионы, города, виды деятельности и т.д.) [6], а для разных временных периодов - как процентное изменение среднего значения макроэкономического показателя («в % к соответствующему периоду предыдущего года»[5]).
Однако использование среднеарифметических значений правомерно только в том случае, когда анализируемое эмпирическое распределение имеет нормальное распределение в виде колоколообразной кривой, когда 68,3% значений распределения лежат в интервале: среднее значение плюс (минус) стандартное отклонение [1, с. 188]. Строго говоря, только в этом случае среднее арифметическое значение эмпирического распределения может быть использовано в качестве макроэкономического индикатора, а его процентное изменение за определенный временной интервал как характеристика различия или темп роста (убыли).
Цель исследования
Цель данной работы заключалась в проверке соответствия эмпирических распределений макроэкономических индикаторов уровня жизни населения России нормальному закону распределения для доказательства правомерности (или неправомерности) использования средних арифметических значений распределений и выборе вида для их графических иллюстраций.
Метод исследования
Для настоящего исследования были выбраны макроэкономические индикаторы уровня жизни субъектов РФ в 2011 году: среднедушевые денежные доходы населения (руб. в месяц), численность занятых в экономике, приходящихся на одного пенсионера (чел. на 1 пенсионера), численность пенсионеров на 1000 чел. населения). Проверка соответствия эмпирических распределений нормальному закону распределения проводилась в программе Statistica 6.0 [4; 7] с помощью критерия Колмогорова-Смирнова (K-Stest) и критерия Шапиро-Уилки (SW-Wtest) [3, c. 41].
Результаты исследования и их обсуждение
По данным Росстата [5] на графике рис. 1 построена гистограмма распределения среднедушевых денежных доходов населения субъектов РФ, на котором также приведен график нормального распределения (распределения Гаусса).
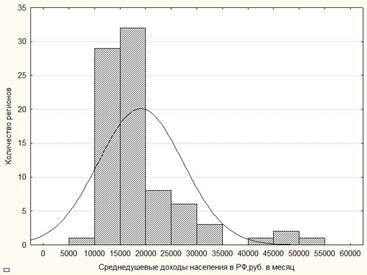
Рис. 1. Гистограмма распределения среднедушевых денежных доходов населения в 83 субъектах РФ в 2011 году [5] (сплошная линия – нормальное распределение).
Как видно из этого графика, распределение среднедушевых денежных доходов населения в субъектах РФ не является нормальным распределением, и поэтому утверждение о том, что «в среднем в РФ среднедушевые денежные доходы населения в 2011 году составляли 19373 руб.» (табл. 2), не корректно. Этот же вывод подтверждают результаты расчетов критериев Колмогорова-Смирнова и Шапиро-Уилки, приведенные в таблице 1.
Так как нормальное распределение для уровня значимости р=0,05 (95% уровень достоверности) имеет место тогда, когда K-S ≤0,0895 и SW-W≥0,947 [3, с. 43], то из данных таблицы 1 видно, что анализируемое эмпирическое распределение не является нормальным распределением и к нему такие показатели описательной статистики, как среднее арифметическое значение, стандартное отклонение, доверительный интервал, и процентные различия средних значений, как темпы роста, не применимы.
Аналогично проведено исследование другого распределения уровня жизни населения: численность занятых в экономике, приходящихся на одного пенсионера, гистограмма которого показана на рис. 2, а в таблице 1 приведены рассчитанные статистические критерии.
Таблица 1 - Проверка нормальности распределений макроэкономических индикаторов РФ для уровня значимости р=0,05
|
Наименование индикатора |
Критерий K-Stest |
Критерий SW-W test |
Вывод |
|
Среднедушевые денежные доходы населения в 2011 г. (руб. в месяц) |
0,235 |
0,692 |
Не является |
|
Численность занятых в экономике в 2011 г., приходящихся на одного пенсионера (чел./чел.) |
0,162 |
0,834 |
Не является |
|
Численность пенсионеров на 1000 человек населения в 2011г. (чел./1000 чел.) |
0,984 |
0,059 |
Является |
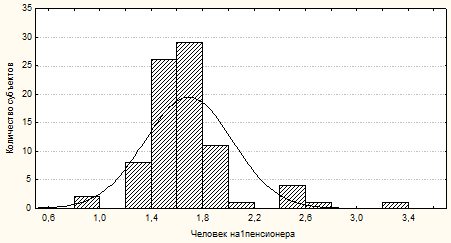
Рис. 2. Гистограмма эмпирического распределения численности занятых в экономике, приходящихся на 1 пенсионера в 83 субъектах РФ в 2011 году [5] (сплошная линия – нормальное распределение).
Как наглядно видно из рис. 2 и расчетных данных в таблице 1, эмпирическое распределение численности занятых в экономике, приходящихся на 1 пенсионера, в субъектах РФ, не является нормальным распределением, и поэтому утверждение о том, что «в среднем в РФ на 1 пенсионера в 2011 году приходилось 1,69 занятых в экономике», не корректно.
По данным Росстата [5] на рис. 3 построена гистограмма еще одного эмпирического распределения - числа пенсионеров на 1000 человек населения в субъектах РФ в 2011 году.
Как видно на графике рис. 3 и из данных в таблице 1, эмпирическое распределение численности пенсионеров на 1000 человек населения в субъектах РФ в 2011 году, в отличие от двух ранее рассмотренных эмпирических распределений, является нормальным распределением, и поэтому утверждение о том, что «в среднем в РФ на 1000 человек населения в 2011 году приходилось 287 пенсионеров», вполне корректно.
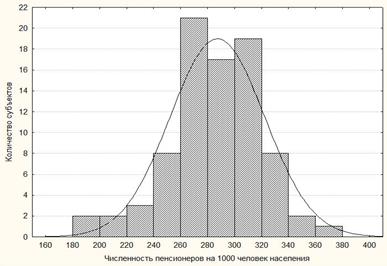
Рис. 3. Гистограмма эмпирического распределения численности пенсионеров на 1000 человек населения в субъектах РФ в 2011 году (сплошная линия – нормальное распределение)
В случае отсутствия нормального распределения более правильно и гораздо более информативно использовать другие показатели описательной статистики, такие как медиана, минимальное и максимальное значение показателя, интерквартильный размах, IQR (разница значений верхнего 75-го нижнего 25-го квартилей) [4, с. 71]. Поэтому в таблице 2 приведены результаты расчетов различных показателей описательной статистики для двух эмпирических распределений.
Таблица 2 - Показатели описательной статистики эмпирических распределений макроэкономических индикаторов РФ в 2011 году
|
Показатель |
Среднее |
Медиана |
Нижний квартиль |
Верхний квартиль |
Размах, IQR |
|
Среднедушевые денежные доходы (руб. в месяц) |
18931 |
16032 |
14353 |
20146 |
5793 |
|
Численность занятых в экономике, приходящихся на 1 пенсионера (чел./чел.) |
1,69 |
1,65 |
1,52 |
1,77 |
0,25 |
Рассчитанные статистические показатели в таблице 2 предоставляют исследователю важную дополнительную информацию для проведения анализа распределений эмпирических данных. Медиана соответствует центру распределения и лучше, чем среднее арифметическое значение, характеризует эмпирическое распределение при асимметричном распределении и малом числе значений в выборке. Так как квартили делят выборку на четыре равные части, то интерквартильный размах (IQR), в котором располагается 50% всех данных, дает ясное представление о ширине распределения и с экономической точки зрения количественно характеризует социально-экономические отличия разных регионов.
Еще одно несомненное преимущество таких статистических показателей, как медиана и квартили, заключается в том, что они не подвержены влиянию выбросов и экстремальных значений, которые всегда имеют место в эмпирическом распределении любого макроэкономического показателя в такой огромной и разноплановой в социальном и экономическом смысле стране, как Россия.
Как видно из данных в таблице 2, в 2011 г. в половине субъектов РФ (41 ФО) среднедушевые доходы населения меньше 16032 руб. в месяц, а в половине (41 ФО) - больше этого размера (значение медианы, median). Кроме того, в половине округов (41 ФО) среднедушевые доходы находились в интервале значений от 14353 до 20145 руб. в месяц (интерквартильный размах, IQR), в то время как «в среднем за период» среднедушевые доходы населения «в среднем» для всех субъектов РФ составляли 18931 руб. в месяц (табл. 2).
При отсутствии нормального распределения данных в качестве графической иллюстрации результатов статистических расчетов целесообразно использовать диаграммы типа «ящик с усами» (Box&Whisker Plot) [4, с. 56], которые обеспечивают большую диагностическую и описательную информацию об исследуемой совокупности эмпирических данных. На рис. 4 и 5 показаны эти диаграммы для двух рассмотренных выше эмпирических распределений.
Как наглядно видно на графике рис. 4, в 2011 г. в половине субъектов РФ (41 ФО) среднедушевые денежные доходы населения были меньше 16032 руб. в месяц, а в половине (41 ФО) - больше этого размера (значение медианы, median). Кроме того, в половине округов (41 ФО) среднедушевые доходы находились в интервале значений от 14353 до 20145 руб. в месяц (IQR=25 – 75%).
Кроме того, на диаграмме рис. 4 обращают на себя внимание большие «усы» (Non-OutlierRange), которые свидетельствуют о широком разбросе среднедушевых денежных доходов населения в субъектах РФ (от 8829 до 25995 руб. в месяц), которые вместе с выбросами и экстремальными значениями, отражая социально-экономическую неоднородность нашей страны, являются причиной отклонения эмпирического распределения от нормального распределения.
Для эмпирического распределения, показанного на рис. 2 и на диаграмме рис. 5, можно сделать следующие выводы. Как видно на графике рис. 5, в 2011 г. в половине субъектов РФ (41 ФО) численность занятых в экономике, приходящихся на 1 пенсионера, была меньше 1,65, а в половине (41 ФО) - больше этой величины (значение медианы).
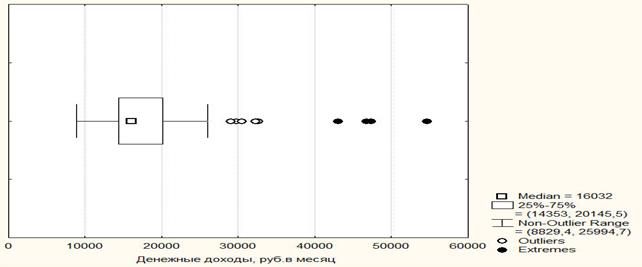
Рис. 4. Диаграмма «ящик с усами» распределения среднедушевых денежных доходов населения в 83 субъектах РФ в 2011 г.
Кроме того, в половине округов (41 ФО) численность занятых в экономике, приходящихся на 1 пенсионера, находилась в интервале значений от 1,52 до 1,77 (IQR=25 – 75%), в то время как «в среднем за период» численность занятых в экономике, приходящихся на 1 пенсионера, «в среднем» для всех субъектов РФ составляла 1,69 (табл. 2).
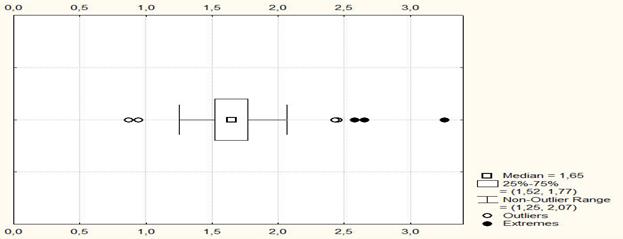
Рис. 5. Диаграмма «ящик с усами» распределения численности занятых в экономике, приходящихся на 1 пенсионера в 83 субъектах РФ в 2011 году.
На диаграмме рис. 5 обращают на себя внимание большие «усы» (Non-OutlierRange), которые свидетельствуют о широком разбросе численности занятых в экономике, приходящихся на 1 пенсионера в субъектах РФ (от 1,25 до 2,07). Также на рис. 5 видны выбросы (Outliers) и значительные экстремальные значения (Extremes), что лишний раз подтверждает большую неоднородность данного макроэкономического индикатора для всех субъектов РФ.
В заключение нелишне заметить, что в научном плане такой использованный в данном исследовании метод статистического анализа эмпирических выборок уже много лет строго регламентирован для зарубежных медиков-исследователей, применяющих медицинскую статистику для обработки данных медико-биологических исследований, эмпирические распределения которых отличаются (как и в экономике) большим разбросом значений и малыми выборками [2, с. 36; 3, с. 31].
Выводы
На основе выполненного исследования можно сделать следующие выводы.
1. Прежде чем использовать среднеарифметические значения в качестве характеристик эмпирических распределений макроэкономических индикаторов, необходимо проверять эти распределения на нормальность (распределение Гаусса).
2. Показано, что такие эмпирические распределения макроэкономических показателей, как среднедушевые денежные доходы населения, численность занятых в экономике, приходящихся на 1 пенсионера, не отвечают закону нормального распределения, и поэтому для их характеристики неправомерно использовать средние арифметические значения и процентные изменения их средних значений.
3. Более информативно и правильно в случае отсутствия нормального распределения для характеристики эмпирического распределения макроэкономических индикаторов использовать такие показатели описательной статистики, как медиана и интерквартильный размах, а в качестве графической иллюстрации – диаграммы типа «ящик с усами».
Рецензенты:
Рогачев А.Ф., д.т.н., профессор, заведующий кафедрой математического моделирования и информатики ФБГОУ ВПО «Волгоградский государственный аграрный университет (ВолГАУ), г. Волгоград.
Московцев А.Ф., д.э.н., профессор, заведующий кафедрой «Менеджмент, маркетинг и организация производства» ФБГОУ ВПО «Волгоградский государственный аграрный университет (ВолГАУ), г. Волгоград.
Библиографическая ссылка
Дарманян А.П. СТАТИСТИЧЕСКИЕ ОСОБЕННОСТИ ВЫЧИСЛЕНИЯ И ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ МАКРОЭКОНОМИЧЕСКИХ ИНДИКАТОРОВ УРОВНЯ ЖИЗНИ НАСЕЛЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8573 (дата обращения: 09.03.2026).



