Введение
При планировании воздушных перелетов большое внимание уделяется безопасности полетов. Статистические исследования показали, что на безопасность полетов в значительной мере оказывает влияние возраст КВС [4, 5]. Следовательно, с целью повышения безопасности полетов руководству авиакомпании необходимо учитывать возраст КВС при управлении штатом сотрудников. При этом возникает задача нахождения достаточно сложного компромисса: набор молодых пилотов обеспечивает увеличение числа пилотов среднего возраста с минимальной аварийностью по истечению некоторого времени их работы, но ведет к увеличению аварийности из-за роста числа малоопытных КВС. Задачей является нахождение оптимальных параметров кадровой политики АК, обеспечивающих снижение аварийности по фактору «человек» [3]. Решается эта задача методами имитационного стохастического моделирования, включающими в себя формальное построение математической модели, ее алгоритмизацию, нахождения оптимальных параметров кадровой политики (являющейся, по–существу, управлением в системе) методами стохастического имитационного моделирования.
Стохастическая имитационная модель политики приема и ухода КВС
Построим формальную математическую модель политики в терминах точечных процессов. Пусть в момент времени 
число людей в АК в возрасте до 
включительно равно 
(время будем считать непрерывным). Запишем балансовое соотношение, основываясь на том, что в каждый момент времени 
количество вновь пришедших людей в возрастном диапазоне 
равно 
(т.е. 
– число людей поступивших в структуру до момента при условии, что их возраст не превышал 
на момент прихода). Число ушедших из структуры 
к моменту времени в возрастном диапазоне равно 
. Тогда имеет место следующее балансовое соотношение:
(1)
где 
для любого .
Процессы и являются семимартингальными с компенсаторами
(2)
(3)
(основные определения и термины для описания семимартингалов см. в [2]), соответственно 
– область определения.
Обозначим 
, 
– минимальный и максимальный допустимые возраста КВС; 
– время, начиная с которого сотрудники начнут достигать максимально допустимого возраста. Область определения E функций 
и 
представлена на рисунке 1.
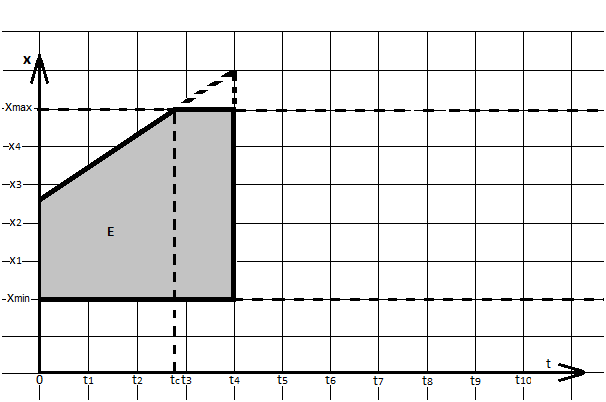
Рисунок 1. Область определения функций , , по оси абсцисс представлено время, по оси ординат возраст КВС
С учетом области определения уравнения (2) и (3) перепишутся в виде
(2*)
(3*)
(4)
Обозначим необходимое количество КВС для управления всеми ВС, обеспечивающих полную загрузку ВС без простоев ВС через 
. Введем также понятия политики приема компании и политики ухода (естественного и увольнения), выражающихся в предпочтении одной возрастной категории КВС над другой. Для этого разобьем интервал [,
) на 
непересекающихся интервалов: [
), 
.
Обозначим политику, в соответствии с которой принимаются новые сотрудники за
, 
, (5)
где 
– максимальное значение весового коэффициента.
И ухода как
, 
, 
(6)
Тогда и будут равны
(7)
(8)
где 
– скорость, с которой восполняют нехватку КВС; 
– скорость ухода (увольнения) КВС; здесь и далее под 
будет пониматься 
.
Целью данной работы является нахождение оптимальных параметров 
и 
кадровой политики АК, обеспечивающих снижение аварийности по фактору «человек».
Стохастическая имитационная модель изменения вероятности АП в зависимости от возраста
В работе [1] было подробно изложено, как получить оценки вероятностей АП 
, на основе статистики взятой из [4].
Количество человек в каждой возрастной группе на момент времени t будет
, (9)
Разделив каждое из значений (9) на их сумму
, (10)
получим вероятность того, что возраст КВС принадлежит i-ой возрастной группе
, (11)
Таким образом, по известным
, – эмпирическим вероятностям возникновения АП при условии, что возраст КВС на момент АП принадлежал i-ой возрастной группе
(12)
Поскольку максимальное количество КВС ограничено значением и процесс 
является точечным, то начиная с некоторого момента 
распределение вероятностей 
,
будет иметь стационарное распределение. Поэтому в формуле (12) будем полагать, что 
.
Кроме того, в качестве вероятностей 
будем брать усредненное значение, построенное по L траекториям процесса .
(13)
Безусловная вероятность наступления АП в формуле (13) зависит от политики приема КВС 
, и политики ухода 
,
см. формулу (6). Необходимо оценить весовые коэффициенты 
, при которых значение вероятности (13) было бы минимальным. Т. е.
(14)
При этом полагается, что параметры 
будут неуправляемые. В качестве них в имитационной компьютерной модели используются их оценки 
, полученные из статистики некоторой авиакомпании.
Расчет оптимальных весовых коэффициентов кадровой политики приема
В соответствии со статистикой, приведенной в таблице 2, все КВС поделены на 8 возрастных групп (
, 
в предположении, что не бывает КВС в возрасте меньше 25 лет, 
). Имеется статистика ухода (увольнения) КВС некоторой авиакомпании в процентном соотношении, сгруппированная по возрастным группам (рисунок 2).
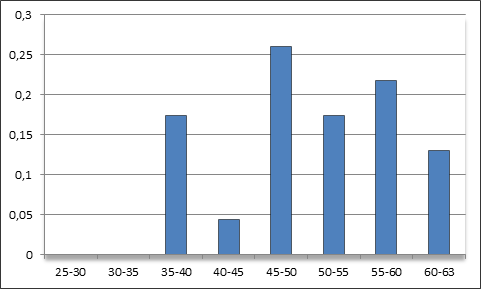
Рисунок 2. Статистика ухода (увольнения) КВС некоторой авиакомпании в период с 2005 по декабрь 2012 года
Имеющиеся процентные соотношения были приняты в качестве весовых коэффициентов политики ухода , формулы (6).
Проведено имитационное моделирование и построены оценки весовых коэффициентов . Начальное значение процесса 
для любого . Из статистических данных одной авиакомпании были выбраны параметры , 
и см формулы (7) и (8). Численность состава КВС составляет 23 человека (
), причем в среднем уходит (увольняется) 3 – 4 человека в год, таким образом, параметр был выбран равным 1,143. Если количество свободных (неустроенных) пилотов, готовых устроиться, меньше потребностей авиакомпании, то 
, иначе, если количество свободных (неустроенных) пилотов достаточное для нужд авиакомпании и компания испытывает острую нехватку в КВС, тогда параметр 
. В данном исследовании ограничений на КВС нет, и компания не испытывает острой нехватки в КВС, поэтому принят равным 1. Момент времени , начиная с которого процесс становится стационарным, равен 7300.
Значения коэффициентов оптимальной политики, при которых оценка вероятности АП минимальна, зависят от , поэтому моделирование производилось для нескольких значений равных 0.15, 0.2 и 0.3 (таблица 1).
Как видно из таблицы 1 минимальное значение, оценка вероятности АП достигала с параметрами близкими или равными 
. Т. е. при приеме в штат более молодых КВС.
Таблица 1. Зависимость коэффициентов оптимальной политики и минимальной оценки вероятности АП от 
.
|
|
|
|
|
0.15 |
|
|
|
0.2 |
|
|
|
0.3 |
|
|
, 
, 
, 
, 
, 
, 
, 
.
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
Заключение
Результаты, представленные в работе, показывают, что при заданном распределении ухода (увольнения и выхода на пенсию) КВС (см. рисунок 4), кадровой службе при приеме на работу следует отдавать предпочтение специалистам в возрасте от минимального до 
, где 
– округление в большую сторону. В этом случае вероятность возникновения АП по фактору «человек» в долгосрочной перспективе окажется наименьшей.
Работа выполнена в рамках федеральной целевой программы "Научные и научно-педагогические кадры инновационной России" на 2009–2013, а также при поддержке Министерства образования и науки РФ в рамках постановления правительства РФ № 218.
Рецензенты:
Кемер Александр Робертович, доктор физико-математических наук, профессор, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.
Мищенко Сергей Петрович, доктор физико-математических наук, профессор, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.
Библиографическая ссылка
Бутов А.А., Савинов Ю.Г., Санников И.А., Егоров А.Г. МОДЕЛЬ ОПТИМАЛЬНОЙ КАДРОВОЙ ПОЛИТИКИ ПРИЕМА КВС // Современные проблемы науки и образования. 2013. № 1. ;URL: https://science-education.ru/ru/article/view?id=8265 (дата обращения: 11.05.2025).