Введение
Дельта-преобразование является, наряду с более известным z-преобразованием, одним из методов математического описания дискретных систем. Разработанное практически одновременно с z-преобразованием, оно долгое время оставалось мало востребованным, так как невысокое быстродействие вычислительных машин прошлого, применяемых при реализации систем автоматического управления и при цифровой обработке сигналов, не позволяло проявляться главному недостатку z-преобразования, а именно: при стремлении периода дискретизации к нулю корни и полюса системы в z-области стремятся к единице [4]. При ограниченной точности машинного представления чисел различные корни стремятся «слиться» друг с другом и с единицей; динамическая характеристика такой цифровой системы не повторяет характеристику непрерывной и может существенно отличаться от нее [5]. Этим эффектом можно пренебречь, если использовать представление чисел с плавающей точкой. Однако на аппаратном уровне его поддерживает довольно ограниченное число контроллеров. Использование же чисел с плавающей точкой на программном уровне приводит к существенному увеличению времени выполнения программы. В результате разработка цифровой системы управления с малым периодом дискретизации становится труднореализуемой задачей.
В то же время дельта-преобразование не имеет вышеописанного недостатка. При уменьшении периода дискретизации динамическая характеристика такой цифровой системы стремится к характеристике непрерывной. Еще больше повысить эффективность дельта- преобразования можно путем реализации программы не каноническими формами программирования, а так называемым совместным интегрированием, описанным в работе [2]. При этом становится возможным использование 16-битного и даже 8-битного контроллера там, где в случае z-преобразования приемлемую точность давал бы только 32-битный.
Преобразование непрерывных и z-систем в дельта-системы
Основная идея дельта-преобразования – использование метода Эйлера для вычисления производной:
, (1)
где 
– период дискретизации.
Как аналог оператора 
введем оператор 
, который имеет следующий смысл:
, (2)
Выведем связь с z-преобразованием. Как известно, его суть состоит в переходе от операции дифференцирования к операции сдвига во времени. Переменная 
при этом обозначает сдвиг во времени на 1 шаг вперед:
(3)
Исходя из (2) и (3), можно записать связь между переменными и :
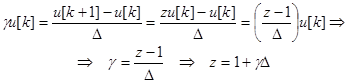(4)
Одним из наиболее удобных способов аппроксимации непрерывной системы, сохраняющей ее устойчивость, является билинейное преобразование, или преобразование Тастина. С учетом выражения (3), можно записать формулу перехода по методу Тастина из s-области в дельта-область:
(5)
В данном случае – период дискретизации при дифференцировании методом Эйлера, а 
– период дискретизации интегрирования, причем они необязательно равны.
С точки зрения инженерной практики, удобно сперва перевести непрерывную систему в z-систему, а затем преобразовать ее коэффициенты таким образом, чтобы заменить оператор 
на. Допустим, у нас имеется дискретная передаточная функция второго порядка:
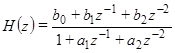(6)
Из формулы (4) известна связь и , откуда следует связь 
и 
:
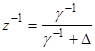(7)
Используя выражения (4) или (7), мы можем преобразовать передаточную функцию дискретной системы к виду:
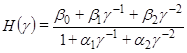(8)
Связь коэффициентов функций в 
и форме представлена в таблице 1.
Таблица 1. Связь коэффициентов дельта и для передаточных функций 2-го порядка
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции более высокого порядка, чем 2-й, на практике лучше реализовать как последовательное соединение функций 1-го и 2-го порядка для уменьшения эффектов округления и переполнения разрядной сетки [1].
Совместное интегрирование
В работе [2] показано, что совместное интегрирование имеет более высокую точность при реализации численных методов интегрирования. Рассмотрим этот метод подробно.
Пусть имеется передаточная функция 
-го порядка, которая была преобразована в систему дифференциальных уравнений 1-го порядка:
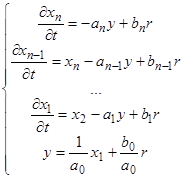(9)
Приведем ее к виду для совместного интегрирования:
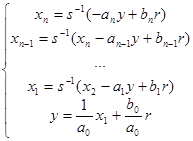(10)
Теперь перейдем от непрерывной системы к дельта-системе. Для этого оператор интегрирования 
заменим на 
. Учитывая, что 
, можно записать:
(11)
Подставляя выражение для 
из системы (10), получим окончательно:
(12)
Проделав аналогичные выкладки для всех уравнений системы (10), нетрудно записать общий вид матриц пространства состояний совместного интегрирования для дельта-системы:
,
,
,
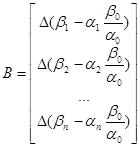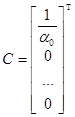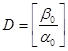(13)
Сравнение z-преобразования и дельта-преобразования на простейшем звене
Возьмем в качестве примера простейшее колебательное звено второго порядка:
(14)
Пусть период дискретизации 
и 
. Тогда в z-области система будет выглядеть так:
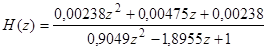(15)
Отсюда, используя формулы из таблицы 1, получим дельта-форму:
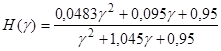(16)
Точные значения коэффициентов переведем в значения с фиксированной точкой при длине машинного слова 16 бит (при этом 14 бит отводятся на запись единицы, то есть 
).
1. Реакция на ступенчатое воздействие
Для анализа дельта-оператора были построены графики z-системы в форме прямого программирования, дельта-системы в форме совместного интегрирования и непрерывной системы. График ошибки моделирования цифровых систем представлен на рисунке 1.
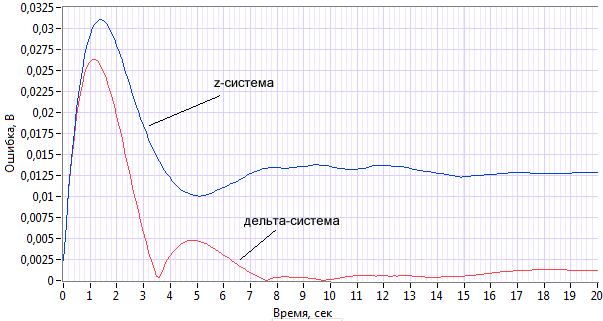
Рисунок 1. Погрешность моделирования переходной характеристики цифровых систем относительно непрерывной системы
Устоявшаяся ошибка в дельта-системе имеет порядок 
, тогда как в z-системе она имеет порядок 
. В то же время при длине машинного слова 16 бит (и из них 14 отведено под дробную часть), коэффициенты системы задаются с точностью порядка
. Таким образом, можно заключить, что одновременное использование дельта-преобразования и совместного интегрирования дает точность выходного сигнала, лишь на два порядка уступающую машинной точности представления чисел, и при этом на порядок точнее, чем использование z-преобразования.
2. Реакция на гармоническое воздействие
Далее исследуем реакцию системы на синусоидальное воздействие. Этот эксперимент особенно показателен в связи с тем, что при конструировании цифровых фильтров чаще всего приходится иметь дело именно с этим классом сигналов.
Пусть период дискретизации и параметр; частота входного синусоидального сигнала выбрана 
(период равен 100 периодам дискретизации). Моделирование проводится при длине машинного слова 16 бит.
На рисунке 2 приведены графики погрешности моделирования z- и дельта-систем относительно выходного сигнала непрерывной системы.
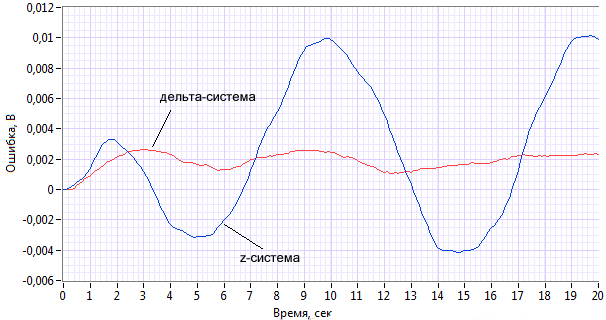
Рисунок 2. Погрешность реакции цифровых систем относительно реакции непрерывной
Для дельта-системы используется совместное интегрирование как более точный метод. Ошибка в этом случае меньше на порядок, как и в случае реакции на единичный скачок.
Сравнения частотных характеристик z- и дельта-систем
Одной из часто используемых систем второго порядка является режекторный фильтр. Он задается передаточной функцией:
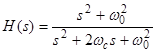(17)
где 
- вырезаемая частота (рад/с), а 
- ширина полосы заграждения. На практике режекторный фильтр применяются чаще всего для отсечения помехи частотой 50±2 Гц. Соответственно, возьмем 
и 
. Тогда функция (34) примет вид:
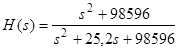(18)
Используя преобразование Тастина, найдем функцию в z-форме:
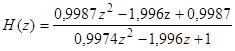(19)
Произведем дельта-преобразование, опираясь на выражение (19):
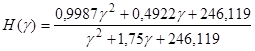(20)
Период дискретизации 
и параметр 
. Моделирование вновь проводится при длине машинного слова 16 бит.
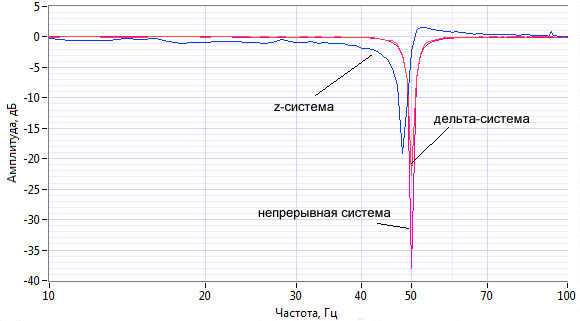
Рисунок 3. АЧХ непрерывного и цифровых режекторных фильтров
Анализ графика АЧХ показывает, что z-система ведет себя неудовлетворительно:
а) подавляемая ею частота составляет 48 Гц, а не 50 Гц;
б) на частоте 51 Гц (входит в область подавления) ее коэффициент усиления больше единицы;
в) АЧХ неровная, имеет побочные пики (например, на частоте 93 Гц).
Таким образом, при 16-битном машинном представлении режекторный фильтр, построенный на основе z-преобразования, имеет неудовлетворительную АЧХ. В то же самое время АЧХ фильтра, построенного на основе дельта-преобразования, очень близка к АЧХ непрерывного фильтра. Более того, в работе [5] показано, что, используя дельта-преобразование, возможна реализация подобного режекторного фильтра даже на 8-битном контроллере.
Заключение
В статье было дано определение дельта-преобразования и рассмотрены способы перехода от непрерывных и z-систем к дельта-системам. Также был предложено объединить метод совместного интегрирования с дельта-преобразованием, позволяющий реализовать дельта-систему на вычислительном устройстве с наиболее высокой точностью.
Было показано, что применение дельта-преобразования и совместного интегрирования при вычислениях с фиксированной точкой позволяет повысить точность вычислений и приблизить цифровую систему по своим характеристикам к непрерывной. В частности, характеристика цифрового запаздывающего звена, построенного на основе дельта-преобразования, на порядок ближе к характеристике непрерывной системы при ступенчатом и синусоидальном воздействиях, чем характеристика z-системы.
Преимущества дельта-преобразования отчетливо проявляются при малых периодах дискретизации. Так, с помощью дельта-преобразования был реализован цифровой режекторный фильтр, который показал значительно лучшие характеристики, чем фильтр на основе z-преобразования.
Работа выполнена при поддержке Министерства образования и науки РФ в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009–2013 годы» (Государственный контракт № 14.B37.21.2021 от 11 ноября 2012 г.).
Рецензенты:
Анисимов Владимир Иванович, д.т.н., профессор кафедры cистем автоматизированного проектирования. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Сольницев Ремир Иосифович, д.т.н., профессор кафедры cистем автоматизированного проектирования. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Андреев В.С., Бутусов Д.Н., Каримов Т.И., Липкин С.М., Сотнин М.И. АНАЛИЗ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ ДЕЛЬТА-ПРЕОБРАЗОВАНИЯ ПРИ МОДЕЛИРОВАНИИ ЗВЕНЬЕВ ВТОРОГО ПОРЯДКА // Современные проблемы науки и образования. – 2013. – № 1. ;URL: https://science-education.ru/ru/article/view?id=8128 (дата обращения: 04.12.2023).