Введение
Взаимодействие атома с электромагнитным полем для энергий фотонов порядка порога ионизации валентных и субвалентных оболочек достаточно хорошо описывается в дипольном приближении. Обычно рассматривается однократная фотоионизация атома или фотовозбуждение одного из его электронов на дискретный уровень. Однако при энергии выше порога двукратной ионизации может также иметь место дву- и более кратная ионизация (возбуждение) атома единичным фотоном. В частности, при достаточно большой энергии ионизирующего излучения, затрагивающего субвалентные и внутренние оболочки атома, процесс множественной ионизации можно достаточно хорошо моделировать многоступенчатым процессом: на первом этапе фотоионизируется внутренняя оболочка, а затем происходит Оже-распад образовавшейся вакансии или даже каскад последовательных Оже-распадов. При энергиях фотона, не затрагивающих напрямую внутренние оболочки, ступенчатая модель уже не имеет места, и множественная ионизация происходит из-за коллективного характера взаимодействия атомных электронов, рис.1. В этом случае энергия возбуждения может быть произвольно распределена между несколькими электронами, покидающими атом при кратной ионизации.
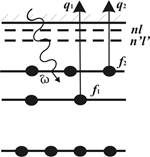
Рис.1. Модель ДФИ
Двукратная фотоионизация (ДФИ) атома изучалась экспериментально и теоретически начиная с конца 1970-х годов. Однако полученные результаты значительно разнятся. По-видимому, наиболее точными являются данные последних лет [2, 3, 9].Поэтому дальнейшее исследование ДФИ остается актуальной задачей.
Основные положения теории
Пусть в результате взаимодействия с фотоном из атома с заполненными оболочками удаляются два электрона q1 и q2 из оболочек f1 и f2. Задавая начальное состояние нулевого приближения волновой функцией основного состояния атома в приближении ХФ, ![]() (вакуумное состояние), конечное состояние можно построить в виде
(вакуумное состояние), конечное состояние можно построить в виде ![]() , где
, где ![]() и
и ![]() – операторы рождения дырок и частиц. При построении
– операторы рождения дырок и частиц. При построении ![]() в приближении LS-связи примем следующий порядок сложения угловых моментов:
в приближении LS-связи примем следующий порядок сложения угловых моментов: ![]() . Здесь LicSic– терм иона-остатка, LqSq– орбитальный и спиновый моменты пары фотоэлектронов. LS=1Pдля атома с заполненными оболочками.
. Здесь LicSic– терм иона-остатка, LqSq– орбитальный и спиновый моменты пары фотоэлектронов. LS=1Pдля атома с заполненными оболочками.
Канальное дифференциальное сечение ДФИ фотоном с энергией ωвыражается через парциальные амплитуды М
![]() . (1)
. (1)
Здесь ε1, ε2и ![]() и
и ![]() – энергии и орбитальные моменты фотоэлектронов, с=137 – скорость света,
– энергии и орбитальные моменты фотоэлектронов, с=137 – скорость света, ![]() – потенциал двукратной ионизации атома (используется атомная система единиц). Полное дифференциальное сечение является суммой канальных сечений
– потенциал двукратной ионизации атома (используется атомная система единиц). Полное дифференциальное сечение является суммой канальных сечений
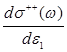 =
=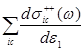 =
=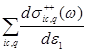 . (2)
. (2)
Полное абсолютное сечение ДФИ является интегральной характеристикой вида 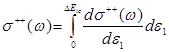 . Энергия перехода
. Энергия перехода ![]() , как отмечено выше, может распределяться между фотоэлектронами произвольным образом.
, как отмечено выше, может распределяться между фотоэлектронами произвольным образом.
M1 =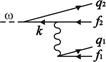 M2 =
M2 =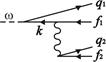
M3 = 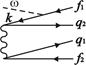 M4 =
M4 =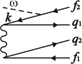
Рис. 2. Диаграммы для ДФИ (плюс обменные).
В низшем неисчезающем порядке теории возмущений (ТВ) по остаточному взаимодействию ![]() амплитуда ДФИ-перехода равна сумме вкладов, графически представленных фейнмановскими диаграммами на рис. 2. Им соответствуют аналитические выражения – парциальные амплитуды
амплитуда ДФИ-перехода равна сумме вкладов, графически представленных фейнмановскими диаграммами на рис. 2. Им соответствуют аналитические выражения – парциальные амплитуды
M1 =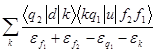 , M2 =
, M2 =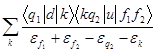 ,
,
M3=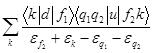 , M4 =
, M4 =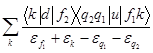 ,
,
где суммирование по k={nklk,mk,μk} проводится по всем дырочным (k![]() F) и частичным (k>F) состояниям, включая интегрирование по непрерывному спектру.
F) и частичным (k>F) состояниям, включая интегрирование по непрерывному спектру.
Окончательные формулы для парциальных амплитуд получены в методике, изложенной в [1], и выражаются через nj-символы и приведенные дипольные и кулоновские матричные элементы. Для примера, угловые множители имеют вид
![]()
![]() ,
,
![]()
![]() ,
,
где Y(0)=![]() , [a]=(2a+1)1/2. Они определяют правила отбора по одноэлектронным
, [a]=(2a+1)1/2. Они определяют правила отбора по одноэлектронным ![]() и промежуточным
и промежуточным ![]() моментам.
моментам.
Следует отметить специфичную трудность при расчете вклада парциальных амплитуд M1, и M2 от промежуточных состояний p1 и p2 непрерывного спектра, связанную с вычислением приведенного дипольного матричного элемента вида ![]() . Такие интегралы расходятся в силу sin-образного асимптотического поведения радиальной части функций непрерывного спектра, но эта проблема оказалась преодолимой.
. Такие интегралы расходятся в силу sin-образного асимптотического поведения радиальной части функций непрерывного спектра, но эта проблема оказалась преодолимой.
При расчете сечений ДФИ в ХФ базисе строгое определение потенциала, в котором движутся фотоэлектроны, оказывается неоднозначным в силу невозможности вычислять ВФ двух фотоэлектронов одновременно, хотя каждый фотоэлектрон движется не только в поле V(N-2) двукратного иона-остатка, но и в поле второго фотоэлектрона. Можно предполагать, что при малых расстояниях между фотоэлектронами, а также вблизи ядра суммарный потенциал похож на V(N-1), а по мере удаления электронов от ядра и друг от друга он стремится к V(N-2). К тому же, медленный электрон экранирует поле двухзарядного иона, в результате чего быстрый электрон движется в поле с потенциалом, похожим на V(N-1). Напротив, медленный электрон движется в поле, близком к V(N-2). Ситуация может еще более усложняться из-за анизотропии углового распределения фотоэлектронов.
Основные результаты и выводы
Ниже представлены результаты расчета сечений ДФИ внешних оболочек неона, полученные с использованием потенциалов V(N-1) и V(N-2) для каждого из фотоэлектронов, и выполнен их сравнительный анализ. Рассмотрены переходы в шесть LS-состояний 1s22s22p4[3P,1D,1S], 1s22s12p5[3P,1P] и 1s22s02p6[1S]. Возможно и формирование короткоживущих возбужденных состояний Ne++ конфигураций 1s22s22p3nl, 1s22s12p4nl, 1s22s02p5nl, когда возбуждается сразу 3 электрона, что гораздо менее вероятно. Здесь такие каналы ДФИ не рассматриваются. Относительные вклады канальных сечений ηic(%) в полные абсолютные V(N-1)и V(N-2)-сечения при выбранных значениях энергии ωвозбуждающего фотона и относительные вклады ηq1,q2 (%) компонент в сечения каналов приведены в таблицах 1 и 2, соответственно, ![]() – потенциалы двукратной ионизации.
– потенциалы двукратной ионизации.
Таблица 1. Относительные вклады ηicканальных сечений в полное абсолютное V(N-1)-сечение ДФИ неона при ω=110.8 эВ и ω=217.0 эВ и относительные вклады ηq1,q2 компонент в сечения каналов при ![]() =5 эВ, 50 эВ и 100 эВ
=5 эВ, 50 эВ и 100 эВ
|
Состояние |
|
Фотоэлектронная |
ω, эВ |
|
|||
|
конечного |
|
пара |
110.8 |
217.0 |
5.0 |
50.0 |
100.0 |
|
иона |
|
(q1,q2) 2S+1L |
ηic(%) |
ηq1,q2 (%) |
|||
|
2s22р4 [3Р] |
62.53 |
(s,p) 3P |
28.5 |
28.0 |
14.6 |
4.3 |
3.1 |
|
|
|
(p,d) 3P, 3D |
|
|
74.9 |
66.7 |
58.7 |
|
|
|
(d,f) 3P, 3D |
|
|
10.6 |
28.7 |
37.3 |
|
|
|
(f,g) 3P, 3D |
|
|
0.1 |
0.3 |
0.8 |
|
|
|
(g,h) 3P, 3D |
|
|
<0.1 |
<0.1 |
0.2 |
|
2s22p4[1D] |
65.73 |
(s,p) 1P |
49.9 |
32.4 |
7.5 |
2.5 |
2.5 |
|
|
|
(p,d) 1P, 1D, 1F |
|
|
77.8 |
70.6 |
61.0 |
|
|
|
(d,f) 1P, 1D, 1F |
|
|
6.3 |
15.9 |
24.5 |
|
|
|
(f,g) 1P, 1D, 1F |
|
|
<0.1 |
0.2 |
0.7 |
|
|
|
(g,h) 1P, 1D, 1F |
|
|
<0.1 |
<0.1 |
0.1 |
|
|
|
(s,f) 1F |
|
|
8.0 |
9.6 |
9.2 |
|
|
|
(P,g) 1F |
|
|
0.2 |
1.1 |
1.6 |
|
|
|
(d,h) 1F |
|
|
<0.1 |
0.1 |
0.4 |
|
2s22p4 [1S] |
69.44 |
(s,p) 1P |
14.8 |
13.4 |
81.6 |
26.2 |
19.6 |
|
|
|
(p,d) 1P |
|
|
11.5 |
44.2 |
39.9 |
|
|
|
(d,f) 1P |
|
|
6.9 |
29.2 |
39.2 |
|
|
|
(f,g) 1P |
|
|
<0.1 |
0.3 |
1.1 |
|
|
|
(g,h) 1P |
|
|
<0.1 |
<0.1 |
0.2 |
|
2s12p5 [3P] |
87.93 |
(s,s) 3S |
3.4 |
10.5 |
<0.1 |
0.4 |
0.3 |
|
|
|
(p,p) 3S, 3P, 3D |
|
|
89.8 |
79.8 |
78.4 |
|
|
|
(d,d) 3S, 3P, 3D |
|
|
1.6 |
7.1 |
7.4 |
|
|
|
(f,f) 3S, 3P, 3D |
|
|
<0.1 |
0.1 |
0.3 |
|
|
|
(g,g) 3S, 3P, 3D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(h,h) 3S, 3P, 3D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(s,d) 3D |
|
|
8.5 |
10.4 |
9.2 |
|
|
|
(p,f) 3D |
|
|
0.2 |
1.4 |
2.9 |
|
|
|
(d,g) 3D |
|
|
<0.1 |
0.9 |
1.5 |
|
|
|
(f,h) 3D |
|
|
<0.1 |
<0.1 |
0.1 |
|
2s12p5 [1P] |
98.42 |
(s,s) 1S |
3.4 |
11.7 |
1.0 |
1.4 |
1.3 |
|
|
|
(p,p) 1S, 1P, 1D |
|
|
87.6 |
49.6 |
47.0 |
|
|
|
(d,d) 1S, 1P, 1D |
|
|
8.9 |
32.7 |
28.6 |
|
|
|
(f,f) 1S, 1P, 1D |
|
|
<0.1 |
0.3 |
1.0 |
|
|
|
(g,g) 1S, 1P, 1D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(h,h) 1S, 1P, 1D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(s,d) 1D |
|
|
1.0 |
11.3 |
13.3 |
|
|
|
(p,f) 1D |
|
|
0.5 |
4.0 |
6.2 |
|
|
|
(d,g) 1D |
|
|
<0.1 |
0.8 |
2.5 |
|
|
|
(f,h) 1D |
|
|
<0.1 |
<0.1 |
0.1 |
|
2s02p6 [1S] |
121.90 |
(s,p) 1P |
0.0 |
4.0 |
99.8 |
76.9 |
61.4 |
|
|
|
(p,d) 1P |
|
|
0.2 |
22.3 |
36.0 |
|
|
|
(d,f) 1P |
|
|
<0.1 |
0.8 |
2.6 |
|
|
|
(f,g) 1P |
|
|
<0.1 |
<0.1 |
0.1 |
|
|
|
(g,h) 1P |
|
|
<0.1 |
<0.1 |
<0.1 |
Таблица 2. Относительные вклады ηicканальных сечений в полное абсолютное V(N-2)-сечение ДФИ неона при ω=111.4 эВ и ω=300.0 эВ и относительные вклады ηq1,q2 компонент в сечения каналов при ![]() =5 эВ, 50 эВ и 100 эВ
=5 эВ, 50 эВ и 100 эВ
|
Состояние |
|
Фотоэлектронная |
ω, эВ |
|
|||
|
конечного |
|
пара |
111.4 |
300.0 |
5.0 |
50.0 |
100.0 |
|
иона |
|
(q1,q2) 2S+1L |
ηic(%) |
ηq1,q2 (%) |
|||
|
2s22р4 [3Р] |
62.53 |
(s,p) 3P |
32.7 |
29.0 |
6.7 |
2.9 |
2.6 |
|
|
|
(p,d) 3P, 3D |
|
|
89.9 |
94.0 |
93.8 |
|
|
|
(d,f) 3P, 3D |
|
|
3.4 |
2.7 |
2.9 |
|
|
|
(f,g) 3P, 3D |
|
|
0.1 |
0.4 |
0.7 |
|
|
|
(g,h) 3P, 3D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
2s22p4[1D] |
65.73 |
(s,p) 1P |
44.9 |
35.4 |
5.8 |
3.2 |
3.4 |
|
|
|
(p,d) 1P, 1D, 1F |
|
|
81.6 |
86.8 |
85.4 |
|
|
|
(d,f) 1P, 1D, 1F |
|
|
4.8 |
3.5 |
3.7 |
|
|
|
(f,g) 1P, 1D, 1F |
|
|
0.1 |
0.4 |
0.8 |
|
|
|
(g,h) 1P, 1D, 1F |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(s,f) 1F |
|
|
7.4 |
5.2 |
5.2 |
|
|
|
(P,g) 1F |
|
|
0.3 |
0.8 |
1.2 |
|
|
|
(d,h) 1F |
|
|
<0.1 |
0.2 |
0.3 |
|
2s22p4 [1S] |
69.44 |
(s,p) 1P |
11.6 |
11.3 |
68.9 |
18.8 |
17.9 |
|
|
|
(p,d) 1P |
|
|
25.7 |
77.0 |
77.2 |
|
|
|
(d,f) 1P |
|
|
5.0 |
2.8 |
2.9 |
|
|
|
(f,g) 1P |
|
|
0.4 |
1.4 |
2.0 |
|
|
|
(g,h) 1P |
|
|
<0.1 |
<0.1 |
0.1 |
|
2s12p5 [3P] |
87.93 |
(s,s) 3S |
4.2 |
8.4 |
<0.1 |
0.3 |
0.4 |
|
|
|
(p,p) 3S, 3P, 3D |
|
|
69.9 |
64.4 |
56.3 |
|
|
|
(d,d) 3S, 3P, 3D |
|
|
28.1 |
19.3 |
17.7 |
|
|
|
(f,f) 3S, 3P, 3D |
|
|
<0.1 |
0.3 |
0.5 |
|
|
|
(g,g) 3S, 3P, 3D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(h,h) 3S, 3P, 3D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(s,d) 3D |
|
|
1.8 |
14.0 |
23.9 |
|
|
|
(p,f) 3D |
|
|
0.2 |
1.6 |
0.9 |
|
|
|
(d,g) 3D |
|
|
<0.1 |
0.1 |
0.3 |
|
|
|
(f,h) 3D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
2s12p5 [1P] |
98.42 |
(s,s) 1S |
6.6 |
12.5 |
1.0 |
1.5 |
1.6 |
|
|
|
(p,p) 1S, 1P, 1D |
|
|
43.3 |
41.4 |
44.3 |
|
|
|
(d,d) 1S, 1P, 1D |
|
|
51.3 |
33.4 |
23.8 |
|
|
|
(f,f) 1S, 1P, 1D |
|
|
0.1 |
0.5 |
0.7 |
|
|
|
(g,g) 1S, 1P, 1D |
|
|
<0.1 |
<0.1 |
0.1 |
|
|
|
(h,h) 1S, 1P, 1D |
|
|
<0.1 |
<0.1 |
<0.1 |
|
|
|
(s,d) 1D |
|
|
3.3 |
19.4 |
24.5 |
|
|
|
(p,f) 1D |
|
|
1.1 |
3.4 |
4.4 |
|
|
|
(d,g) 1D |
|
|
<0.1 |
0.3 |
0.6 |
|
|
|
(f,h) 1D |
|
|
<0.1 |
<0.1 |
0.1 |
|
2s02p6 [1S] |
121.90 |
(s,p) 1P |
0.0 |
3.7 |
93.2 |
65.6 |
57.2 |
|
|
|
(p,d) 1P |
|
|
6.6 |
33.0 |
39.5 |
|
|
|
(d,f) 1P |
|
|
0.1 |
1.4 |
3.1 |
|
|
|
(f,g) 1P |
|
|
<0.1 |
0.1 |
0.3 |
|
|
|
(g,h) 1P |
|
|
<0.1 |
<0.1 |
<0.1 |
Видно, что пары (компоненты), включающие фотоэлектрон с орбитальным моментом l>5, дают пренебрежимо малый вклад в абсолютные канальные сечения, поэтому в их расчете такие фотоэлектроны не учитывались. Однако относительный вклад ηq1,q2 фотоэлектронных пар с высшими моментами имеет тенденцию к возрастанию с увеличением энергии фотона. Так, при ω=320 эВ некоторые компоненты еще не достигают своего максимума. Таким образом, абсолютные сечения несколько недооценены для высоких энергий фотона. Рассчитанные полные абсолютные V(N-1) и V(N-2)-сечения ДФИ в формах длины и скорости в сравнении с экспериментальными и теоретическими данными других авторов приведены на рис.2.
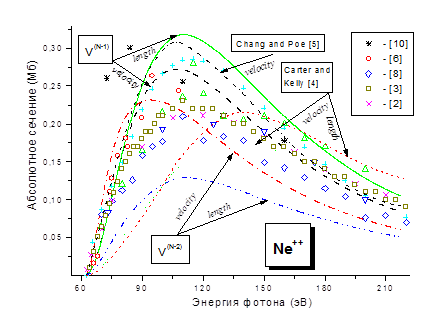
Рис. 3. Экспериментальные и расчетные сечения ДФИ
Отметим, что V(N-1)-потенциал дает хорошее согласие с экспериментом по энергетическому положению максимума сечения, но значительно переоценивает как само сечение в области от 30–150 эВ выше порога, так и его максимум. Вычисленные V(N-2)-сечения оказались значительно меньше V(N-1)-сечений, что физически вполне оправдано большей локализацией V(N-2)-потенциала и, как следствие, более сильным притяжением фотоэлектронов к иону-остатку. Наименьшим оказалось V(N-2)-сечение в форме длины (σ++max=0.13 Мб при ω=112 эВ), в 2–2.5 раза меньше V(N-1)-сечения. Подводя итог, нужно отметить большое различие между полными абсолютными сечениями 4-х вариантов расчета, особенно между V(N-1)- и V(N-2)-сечениями в форме длины. При этом выявляются следующие характерные черты:
– обе формы ![]() -сечений заметно меньше сечений
-сечений заметно меньше сечений ![]() ;
;
– V(N-1)- и V(N-2)-сечения в форме длины отличаются наиболее значительно, в 2 – 2.5 раза, однако имеют близкое к экспериментальному положение максимумов по энергии;
– значение максимума ![]() -сечения в форме скорости(0.23 Мб при 94 eVдля) хорошо соответствует эксперименту, однако максимум смещен в сторону меньших энергий фотона;
-сечения в форме скорости(0.23 Мб при 94 eVдля) хорошо соответствует эксперименту, однако максимум смещен в сторону меньших энергий фотона;
– в области непосредственно за порогом двукратной ионизации ![]() -сечение в форме скорости лежит выше, а за максимумом – ниже экспериментального;
-сечение в форме скорости лежит выше, а за максимумом – ниже экспериментального;
– почти все экспериментальные точки лежат между ![]() - и
- и ![]() -сечениями в форме длины;
-сечениями в форме длины;
– полные (и канальные) ![]() - и
- и ![]() -сечения в форме скорости лежат между
-сечения в форме скорости лежат между ![]() - и
- и ![]() -сечениями в форме длины.
-сечениями в форме длины.
Таким образом, ни один из вариантов расчета сечений ДФИ не дал полностью удовлетворительного согласия с имеющимися экспериментальными данными. По-видимому, в расчете необходимо учитывать корреляционные поправки высших порядков ТВ. Однако их прямой расчет встречает значительные трудности из-за стремительного увеличения числа диаграмм и многократного интегрирования по промежуточным состояниям. Поэтому имеет смысл разработать метод эффективного учета корреляций высших порядков, оставаясь формально в рамках низшего неисчезающего порядка ТВ. Таковым может быть метод, основанный на использовании потенциала ![]() с вариационным параметром q(1<q<2), ответственным за взаимное экранирование фотоэлектронами кулоновского поля иона-остатка.
с вариационным параметром q(1<q<2), ответственным за взаимное экранирование фотоэлектронами кулоновского поля иона-остатка.
Рецензенты:
Шаповалов А. В., д.ф.-м.н., профессор, зав. кафедрой теоретической физики Физического факультета Национального исследовательского Томского государственного университета, г. Томск.
Гриняев С. Н., д.ф.-м.н., доцент кафедры теоретической и экспериментальной физики Физико-технического института Национального исследовательского Томского политехнического университета, г. Томск.
Библиографическая ссылка
Килин В.А., Килин Р.Ю. ОДНОФОТОННАЯ ДВУКРАТНАЯ ИОНИЗАЦИЯ АТОМОВ // Современные проблемы науки и образования. 2012. № 6. ;URL: https://science-education.ru/ru/article/view?id=7927 (дата обращения: 30.12.2025).



